Графические и телесные решения

Информатика

Классы. Часть 2

Поурочные разработки

 

 

Издание разработано при поддержке Отдела теории алгоритмов и математических основ кодирования Вычислительного центра им. А.А. Дородницына Российской академии наук (заведующий отделом — к. ф.-м. н. В. А. Варданян)

 

 

Москва «Просвещение»

Институт новых технологий

Содержание

Предисловие. 4

Способы решения задач. 5

Графические и телесные решения. 11

Комментарии к учебнику. 12

Урок «Длина цепочки». 12

Решение задач 1—6 из учебника. 12

Урок «Цепочка цепочек». 15

Списки и языки программирования. 15

Решение задач 7—13 из учебника. 17

Урок «Таблица для мешка (по двум признакам)». 19

Мешки-векторы.. 19

Решение задач 14— 18 из учебника. 21

Урок «Словарный порядок. Дефис и апостроф». 26

Словарный порядок. 26

Дефис и апостроф.. 27

Решение задач 19—26 из учебника. 29

Урок «Дерево. Следующие вершины, листья. Предыдущие вершины». 33

Решение задач 27—33 из учебника. 35

Уроки «Уровень вершины дерева». 37

Решение задач 34—45 из учебника. 38

Математическое словоупотребление. 38

Проект «Одинаковые мешки». 45

Несколько слов о работе над проектами. 45

Комментарии к проекту «Одинаковые мешки». 47

Первый этап проекта. 47

Второй этап проекта. 50

Уроки «Робик. Команды для Робика. Программа для Робика». 53

Программа для Робика. 54

Решение задач 46—64 из учебника. 55

Уроки «Перед каждой бусиной. После каждой бусины». 65

Решение задач 65—77 из учебника. 65

Проект «Лексикографический порядок». 72

О проекте. 72

Алфавитные линейки. 73

Словари для работы.. 74

Ход проекта. 75

Игры на словарный порядок. 91

Уроки «Склеивание цепочек». 92

Решение задач 78—89 из учебника. 93

Контрольная работа 1. 97

Урок «Выравнивание, решение необязательных и трудных задач». 99

Решение задач 90—102 из учебника. 99

Урок (и) «Путь дерева». 106

Ветвление. 106

Полный перебор и деревья. 107

Решение задач 103—115 из учебника. 108

Компьютерный проект «Определение дерева по веточкам и почкам» (только для компьютерного варианта изучения курса) 116

О проекте. 116

Работа с определителем.. 118

Уроки «Все пути дерева». 119

Решение задач 116—131 из учебника. 120

Урок «Деревья потомков». 128

Решение задач 132—138 из учебника. 129

Проект «Сортировка слиянием». 132

Несколько слов о сортировке информации. 132

Описание проекта. 134

Повторение алфавита. 137

Основной проект. 139

Несколько слов о параллельной организации работы.. 141

Ещё несколько слов о параллельной работе. 147

Список всех слов (в словарном порядке) 154

Дополнительные мини-проекты: сортировка без обязательного упорядочения. 158

Заключение. 162

Уроки «Робик. Конструкция повторения». 163

Решение задач 139—154 из учебника. 163

Уроки «Склеивание мешков цепочек». 172

Решение задач 155—176 из учебника. 173

Урок «Таблица для склеивания мешков». 184

Решение задач 177—183 из учебника. 185

Проект «Турниры и соревнования». 1 часть. 187

Общее обсуждение. 187

Решение задач из тетради проектов. 189

Проект «Турниры и соревнования». 2 часть. 192

Проведение турниров в классе. 192

Дополнение. Игра в камешки. 193

Заключение. 194

Контрольная работа 2. 194

Урок «Выравнивание, решение необязательных и трудных задач». 197

Решение задач 184—201 из учебника. 197

Компьютерный проект «Живая картина» (только для компьютерного варианта изучения курса) 207

О проекте. 208

Общее обсуждение. 208

Знакомство с возможностями использования готовых форм Черепашки. 208

Индивидуальное обсуждение с ребятами эскизов картинок. 211

Планирование работ. 213

Рисование фона. 213

Использование готовых форм Черепашки. 214

Рисование (корректировка) сложных изображений в графическом редакторе. 214

Программирование движения с помощью Черепашки. 215

Просмотр и обсуждение готовых работ. 215

Планирование курса 3 класса. 216

(для бескомпьютерного варианта изучения) 216

 

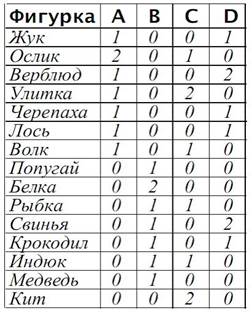
Предисловие

Курс «Информатика. 3 класс» Рудченко Т. А., Семёнова А. Л. является продолжением курсов «Информатика. 1 класс» и «Информатика. 2 класс» тех же авторов и соответственно частью комплекта «Информатика. 1—4 классы» (Рудченко Т. А., Семёнов А. Л.). Курс рассчитан на 1 час в неделю, всего на 34 учебных часа. Как и в 1—2 классах, вы можете выбрать бескомпьютерный или компьютерный вариант работы (варианты соответствующих планирований приведены в конце данной книги). В первом случае дети будут работать только с печатными материалами курса (учебник, рабочая тетрадь и тетрадь проектов). Во втором случае, кроме печатных материалов, можно использовать компьютерную составляющую курса.

Все уроки делятся на обычные и проектные. На обычных уроках дети работают с учебником и рабочей тетрадью, а в случае компьютерного варианта изучения — ещё и с компьютерными уроками. Проекты делятся на компьютерные и бескомпьютерные. В первом случае дети будут выполнять их на компьютере, во втором — будут работать с тетрадью проектов. Компьютерную составляющую для курса «Информатика. 3 класс» можно найти на сайте http://info.seminfo.ru.

Более подробное описание всего курса в целом можно найти в поурочных разработках к курсу «Информатика. 1 класс».

В 3 классе дети продолжают работу с базовыми объектами математической информатики (и всей современной математики) — цепочками и мешками. В курсе появляются новые объекты — деревья и цепочки цепочек. С одной стороны, эти объекты, как говорят математики, являются естественным обобщением цепочек. С другой стороны, они отражают определённые важные свойства мышления, языка и окружающего мира. Объекты и события, входящие в цепочки, могут иметь собственную внутреннюю структуру, а ход событий необязательно будет однозначно заранее предопределён и может «ветвиться». Например, в цепочке дней каждый день является самостоятельной цепочкой событий. Другой пример: отпуск будет проходить так или иначе в зависимости от погоды и других условий.

Дети познакомятся с простейшим исполнителем — Робиком. Робик будет нашим главным партнёром в изучении соответствия между планом и его выполнением.

Способы решения задач

При решении задач из учебника, как и во многих других ситуациях в человеческой практике и в сфере информационных технологий, могут быть использованы различные общие стратегии. Попробуем описать некоторые из них. При этом мы будем использовать «взрослую» терминологию, которую не вводим явно в учебнике. Но вы можете пользоваться этой терминологией при разборе задач с детьми, постепенно приучая их к правильному словесному описанию своей деятельности. По нашему мнению, заучивать абстрактные формулировки стратегий дети не должны — это бесполезно и даже вредно. Определённая польза состоит именно в том, что учащийся открывает эти стратегии самостоятельно, возможно, с помощью учителя, многократно применяет их на практике, постепенно осмысливает и начинает использовать более сознательно и систематически.

Метод последовательного перебора. Метод состоит в том, чтобы последовательно и систематически, в некотором смысле «механически», перебирать все возможные варианты решения. Говорят также о «переборе вариантов» или «переборе возможностей», и мы именно так и будем говорить. Иногда (и не так уж редко) метод последовательного перебора приводит к полному решению задачи. Чаще это позволяет накопить экспериментальный материал для того, чтобы сузить пространство перебора или начать последовательно и направленно идти к ответу, используя уже другие методы.

Часто одна или несколько из рассматриваемых (перебираемых) возможностей сама в свою очередь состоит из последовательности выборов. Например, пытаясь найти выигрышную стратегию в игре, нужно рассматривать все возможные варианты первого хода, затем все возможные варианты хода противника, затем все варианты нашего второго хода и т. д. Тогда для перебора возможностей следует организовать перебор различных последовательностей выборов. Эту ситуацию естественно представлять в виде дерева (с деревьями дети познакомятся в 3 классе). Если при переборе вершин дерева мы окажемся в тупике (это значит, что на данном пути решения нет), возвращаемся на шаг назад и выбираем другую возможность (другую ветку дерева). Исследовав все ветки, выходящие из какой-то вершины, и не найдя решения, возвращаемся ещё на шаг назад и выбираем другую ветку дерева на предыдущем уровне.

Стратегия полного перебора позволяет найти решение, если оно есть. Почему же люди не решают таким образом все задачи? Ответ состоит в том, что перебор почти всегда занимает слишком много времени. Более того, иногда множество, из которого выбираются объекты, бесконечно. Предположим, что для решения какого-то уравнения мы перебираем все целые числа, подставляем их в уравнение, а у уравнения вообще нет решения: в этом случае процесс перебора будет продолжаться бесконечно долго!

Одним из самых замечательных результатов «большой» информатики является открытие того факта, что большое число задач, для которых пока найден только переборный метод решения, в некотором смысле одинаковы (такие задачи иногда называют «переборными»). Специалисты считают, что, скорее всего, ни для одной из них более быстрого способа нахождения ответа не существует. Если бы быстрый способ всё же нашёлся для одной переборной задачи, то он сразу же подошёл бы для всех остальных. Этот замечательный факт был обнаружен на рубеже 70-х гг. ХХ в. одновременно советскими и американскими математиками. Вот пример такой переборной задачи: «Дан мешок натуральных чисел и ещё одно число. Можно ли найти в мешке несколько чисел так, чтобы их сумма была равна этому данному?»

Идея метода полного перебора в какой-то степени противостоит распространённым школьным идеям о правильном первом шаге в решении, об искусственном приёме и т. п. Однако противоречия здесь нет, в действительности и в человеческой практике и при решении учебных задач полезно, а иногда и необходимо использовать и ту и другую стратегии.

Метод проб и ошибок. Идея метода состоит в том, что для накопления экспериментального материала необязательно последовательно и систематически перебирать все возможные варианты ответа. Можно попробовать сделать какой-нибудь шаг, а если выяснится, что результат не достигнут, т. е. произошла ошибка, то сделать какой-то другой шаг. И так пробовать, пока не найдётся ответ, или не сузится пространство перебора, или не найдётся иной подход к решению. Иногда даже один, взятый наугад, случайный вариант ответа (и не подошедший в качестве ответа) позволяет получить достаточно информации, чтобы затем планомерно построить настоящий ответ. Иногда надо попытаться взять случайный, но типичный, или самый простой, или самый сложный объект и попытаться исследовать его и т. д.

Такой способ является очень естественным для детей, хотя обычно и не поощряется школой. В названии способа имеется слово «ошибка», но ничего плохого в этом нет. Нужно приучить ребёнка к тому, что без ошибок никакая человеческая деятельность не обходится, ошибаться не позорно, но надо учиться замечать и исправлять свои ошибки. Это вообще исключительно важно: школа часто выстраивает перед ребёнком идеал безошибочности, что вредит ему в дальнейшей учёбе и в жизни. Возможность ошибиться и затем исправить, найти свою ошибку психологически важна для ребёнка, надо его не ругать за пробы и перебор вариантов, а хвалить.

Данный метод отличается от предыдущего именно тем, что в нём перебор «непоследовательный», так сказать, «хаотичный». Он уже не гарантирует нахождения ответа. Более того, часто бывает, что использующий этот метод человек много раз выбирает бесперспективный путь, «топчется на месте». Почему же всё-таки люди используют такую стратегию, а мы рассматриваем её в своих книгах? Оказывается, что при переборе наугад у человека быстрее включаются на сознательном и подсознательном уровнях алгоритмы выявления закономерностей, позволяющие классифицировать объекты и сокращать перебор, искать более прямой путь к решению. При переборе возможностей накапливается опыт, показывающий, какого типа действия стоит пробовать, а какого нет. И в решении задачи возникнет более экономная стратегия, а может даже появиться и готовое решение задачи, не базирующееся на пробах, а исходящее из понимания того, «как всё на самом деле устроено». Чтобы научить детей правильно использовать такой метод, надо выработать у них привычку анализировать процесс перебора, спрашивать у них, почему они решили попробовать тот или иной вариант, почему вариант не подошёл, все ли подходы учтены и использованы.

В комментариях к задачам учебника мы обсуждаем конкретные закономерности, которые можно найти и использовать в задачах.

Метод Монте-Карло. Можно не стараться угадать, какой объект попробовать в методе проб и ошибок, а действовать наугад, «с закрытыми глазами». Пробуя такие случайные объекты, можно собрать важную информацию, например составить представление о том, сколько решений у данной задачи среди всех возможных, а не просто найти одно решение. Название «Монте-Карло» — это не фамилия автора метода, а отсылка к игорному (случайному) выбору. Чтобы получить случайный объект, например цепочку нулей и единиц, можно бросать монету. Чтобы получить цепочку целых чисел от 1 до 6, можно бросать игральную кость. Чтобы научить компьютер такому случайному выбору, пишут специальные программы. Они позволяют компьютеру создавать объекты (например, числа), похожие на случайные (действительно случайный выбор современному компьютеру недоступен).

Метод сборки снизу вверх (метод «Разделяй и властвуй»). Этот метод состоит в том, чтобы выделить в задаче частичные подзадачи, построить их решения, а потом из них собрать всё решение. С упомянутым подходом тесно связано проектирование сверху вниз, при котором мы сначала описываем нужные нам свойства всего объекта (например, всей программы или всего здания, которое нужно построить), затем разбиваем этот объект на части (например, выделяем подпрограммы или отдельные части здания) так, что если эти части имеют правильные свойства (например, работают или построены правильно), то весь объект будет решением задачи. Так можно поступать и далее, измельчая получающиеся объекты до тех пор, пока не станет совсем ясно, как построить самые мелкие. Название «Разделяй и властвуй» связано с латинским изречением «Dividio et conquar», соответствующим стратегии управления, при которой начальник (император) справляется (расправляется) с отдельными частями управляемой системы (провинциями, вассалами, завоёванными территориями) и в результате управляет целым. При изучении курса дети будут знакомиться с различными применениями метода «Разделяй и властвуй» и будут не раз строить объекты сверху вниз. В вычислительных информатических задачах этот метод реализуется как «метод динамического программирования».

Описанные выше стратегии и методы, конечно, далеко не исчерпывают всех подходов, накопленных человечеством, но они довольно часто будут оказываться полезными детям при решении задач курса, и вы можете их обсуждать с теми учениками, которые начинают активно и систематически их применять.

В задачах и проектах мы уделим много внимания демонстрации способов решения разных типов задач. С одной стороны, формирование эффективных способов решения (эффективных алгоритмов) — важная часть современной науки информатики. С другой стороны, просто рассказывать детям о разных способах и даже демонстрировать их — это дело неэффективное и даже бесполезное. Дети должны не просто быть проинформированы о способах, скажем, сортировки объектов, но и действительно пользоваться ими как при решении задач курса, так и в жизни. Чтобы достичь этого, для начала нужно у каждого ребёнка создать достаточную мотивацию использования того или иного способа действия. Работая с задачами курса, дети постоянно сталкиваются с необходимостью как-то структурировать, планировать свои действия. Не случайно в комментариях к задачам мы часто просим вас дать возможность каждому ребёнку поработать с задачей самостоятельно, даже если вы заранее знаете, что она будет трудна для него. Опыт самостоятельной работы над задачей, поиск решения, изобретение своих собственных способов решения — одни из самых развивающих интеллектуальных действий. При такой работе постепенно формируется ощущение необходимости выработки стратегии решения.

Только после того, как ребёнок накопил достаточный (самостоятельный!) опыт, он сможет понять и принять те методы работы, которые вы ему предложите, скажем, на проектном уроке или при обсуждении решения очередной задачи.

Усвоенный алгоритм работы, например сортировки или попарного сравнения объектов, потом можно реализовывать в формализованном виде с абстрактными математическими объектами. Эта общая схема — отработка алгоритма на видимых осязаемых объектах с последующим переносом на абстрактные математические объекты — используется почти по всему курсу. В 4 классе дети продолжат заниматься проблемами планирования и построения стратегии на примере различных игр.

Мешки-векторы

Ребята уже знакомы с мешками и одномерными таблицами для мешков. Надеемся, что работа с данными математическими объектами не вызовет у них особых трудностей. Однако для математики введение этих объектов оказалось достаточно важным шагом. Дело в том, что числа, прежде всего натуральные, очень удобны для измерений, например, времени (в секундах), или веса (в граммах), или пройденного расстояния (в метрах). Но если мы хотим указать не сколько мы прошли, а куда пришли, то ситуация становится сложнее. Нам приходится указывать два измерения — два числа или два символа. Это похоже на то, как мы указываем положение в городе (например, говорим: «угол Ленина и Розы Люксембург») или поле на шахматной доске (например, e2). Самый распространённый в математике способ состоит в том, что на поверхность наносится сетка, как на бумаге в клетку. Если взять лист клетчатой бумаги, то с каждой клеткой на нём можно сопоставить два натуральных числа. Одно из этих чисел означает, сколько шагов надо сделать из нашей клетки, чтобы оказаться у левого края листа, а другое — сколько шагов надо сделать, чтобы добраться до нижнего края. Два таких числа называют координатами квадрата, их нельзя поменять местами — это не просто мешок, в котором лежат два числа, но упорядоченная пара (цепочка!), о которой мы договорились, что первое число — всегда расстояние до левого края листа, а второе — расстояние до нижнего края.

Тем не менее координаты можно сложить в мешок. Для этого понадобятся бусины двух типов: бусина одного типа будет обозначать один шаг влево, а бусина другого — один шаг вниз. Какими именно будут бусины — вопрос договорённости. Например, квадратными и круглыми или синими и зелёными. А могут быть карточки, на которых написано «Влево» и «Вниз». Таким образом, каждой клетке на листе можно сопоставить мешок, в котором будет некоторое количество бусин «Влево» и некоторое количество бусин «Вниз».

Построив одномерную таблицу для такого мешка, получим пару чисел, аналогичную координатам: ведь в таблице для каждого числа ясно, количество каких именно карточек оно обозначает. Получится так называемый вектор. Конечно, вектор может иметь не только два, но и больше параметров (соответствующая цепочка чисел может быть длиннее). И в нашем мешке могут тоже лежать бусины многих типов. В отличие от множества в мешке (мультимножестве) может быть несколько объектов одного типа. Значит, в таблице для мешка будут не только единицы и нули.

С понятия «вектор» начинается изучение науки, которую называют аналитической геометрией. Данное понятие лежит в фундаменте физики и многих разделов математики.

Тема нового урока — двумерные таблицы для мешков. С научной точки зрения двумерные таблицы — это следующая по сложности структура, набор векторов. Конечно, не нужно сейчас нагружать детей этой сложной терминологией. Достаточно того, что они научатся сортировать и классифицировать элементы мешка по двум признакам и аккуратно заполнять таблицу.

Словарный порядок

На уроках русского языка ребята уже пользовались словарями. И в нашем курсе детям приходилось работать с цепочками слов, расположенными в словарном порядке. Например, во 2 классе ребята решали большую серию задач на работу с учебным словарём. Ни в одной из этих задач не требовалось расположить слова в словарном порядке, тем не менее дети к настоящему моменту приобрели некий опыт, который на этом уроке им предстоит систематизировать и обобщить.

В первой части листа определений содержится общее описание правила словарного порядка. Первый абзац наверняка будет понятен практически всем. Второй и третий абзацы нужно обсудить подробно. При этом можно опираться на пример словарика справа. Так, во время обсуждения можно спросить детей, почему слово ДОЛ идёт раньше слова ДОЛГ, почему слово ДОЛГИЙ идёт раньше слова ДОЛГОВЕЧНОСТЬ и т. д. В каждом из случаев ребёнок должен пояснить, на какое правило из листа определения он опирается и по какой букве идёт упорядочение.

Дальше в задачах цепочку слов, упорядоченных в словарном порядке, мы будем называть словарём.

Дефис и апостроф

Может показаться странным, что мы вводим внутрисловные знаки после того, как дети выполнили проект «Знакомство с русским текстом» (в курсе 2 класса). На самом деле этот лист определений обобщает и систематизирует тот опыт и ту информацию, которые ребёнок уже получил. В традиционных школьных курсах вопрос о статусе дефиса и апострофа обходят стороной. Полагаем, что знание этих знаков и умение их использовать — необходимый элемент языковой культуры. Мы также считаем необходимым, чтобы ребёнок твёрдо уяснил себе не только чисто графические различия между дефисом и тире, но и различие в их статусе: если тире относится к знакам препинания, то дефис по своим функциям скорее похож на букву, чем на знак препинания. Действительно, если знаки препинания ставят между словами и предложениями, то дефис существует только внутри слова. Поэтому его и называют внутрисловным знаком.

Графически апостроф — это запятая вверху строки, содержательно не имеющая ничего общего ни с запятой, ни с каким-либо другим знаком препинания. Так же как и дефис, апостроф существует только внутри слова, выполняя функции буквы. Апостроф чаще встречается в иностранных словах (именах собственных). Одно время он использовался в русском языке вместо твёрдого знака, но об этом говорить детям пока нет необходимости (конечно, если никто из них сам не вспомнит, что у него на доме написано «ПОД’ЕЗД № 2»). Встречаются и «авторские» использования апострофа, например когда «изоб’ажают ка’тавость»; нас такая функция апострофа не интересует. Есть небольшая вероятность того, что кто-то из детей сталкивался с одинарными кавычками — ‘ ’. Полиграфисты называют такие кавычки марровскими. Если такой вопрос возникнет, следует объяснить, что правая марровская кавычка и апостроф — это совсем разные знаки и похожи они случайно (кавычки — парный знак и не внутрисловный).

Таким образом, формально говоря, дефис и апостроф можно отнести к символам алфавита, хотя традиционно алфавит считается состоящим только из букв. Именно поэтому на этом листе определений доопределяется (и расширяется) наше понятие «слово»: в курсе 2 класса слово определялось как любая цепочка букв, и в результате некоторые слова русского языка по нашему определению словами не являлись. Теперь это противоречие снимается — теперь все слова русского языка являются словами и с точки зрения понятий курса информатики. Обратное, конечно же, по-прежнему остаётся неверным. Поэтому основным понятием в задачах остаётся понятие слова как произвольной цепочки букв (и дефиса с апострофом). Если в задаче требуется построить слово, являющееся частью языка, используется выражение «слово русского языка».

Во второй части листа определений тоже имеется небольшой словарь. Выбирая из него пары слов, вы можете проверить, все ли дети правильно понимают, как упорядочиваются слова с дефисом и апострофом. На самом деле для каждого слова с дефисом или апострофом его место в цепочке будет таким же, как если бы в слове этих знаков просто не было. Именно это имеется в виду в тексте листа определений, где говорится, что эти знаки при упорядочивании слов не учитываются.

Первый этап проекта

Учащиеся самостоятельно работают с задачей 1, а также участвуют в общем обсуждении своих действий.

Сначала ребятам предлагается придумать, как (быстрее) отыскать одинаковые мешки в задаче 1. Для этого учащиеся обычно начинают беспорядочно сравнивать пары (ведь именно так они находили одинаковые мешки в задачах учебника). Надо сразу договориться: тот, кто считает, что получил ответ, показывает его только учителю, чтобы не лишать товарищей радости самостоятельного поиска. Кто-то, выбирая пары случайно, найдёт два одинаковых мешка. В этом случае надо попросить удачливого ученика проверить, нет ли здесь ещё одинаковых мешков.

В процессе обсуждения способов сравнения мешков обязательно должен прозвучать вариант составления таблиц мешков. Действительно, сравнить две колонки чисел гораздо легче, чем два беспорядочно уложенных мешка. Каждый мешок нужно представить в виде колонки чисел — какие фигурки и в каком количестве в нём лежат. Но состав фигурок в каждом мешке свой. Можно для начала взять два мешка, скажем мешки А и С (пара А и В не годится, потому что эти мешки вообще не пересекаются), и попытаться сравнить их с помощью составления таблиц. Предложите детям подумать, как составить таблицы для мешков так, чтобы их впоследствии было удобно сравнивать. Если составлять таблицы для А и С по отдельности (дети уже делали это в задачах), то сравнивать их потом будет не намного проще, чем сами мешки. Так постепенно рождается мысль о том, что таблицы мешков должны быть «унифицированы», т. е. список и порядок фигурок для заполнения таблицы каждого мешка должны быть одинаковыми. В таком случае таблицы мешков могут быть колонками одной таблицы, и эти колонки будет легко сравнивать. Самый левый столбец в таблице (шапка) — список всех фигурок, встречающихся в мешках, а в следующих столбцах мы сможем записать, сколько каких фигурок в мешках, т. е. заполнить таблицы для мешков А и С. Если какой-то фигурки в одном из мешков нет, то в соответствующей клетке просто ставим ноль. В ходе разговора на доске появится таблица, похожая на таблицу к задаче 1, но только меньше. Левый столбец таблицы тоже заполняется в ходе просмотра мешков А и С: берём мешок А, выписываем названия всех фигурок, которые там встречаются, затем берём мешок С и дописываем ниже названия тех фигурок, которых в первом столбце таблицы ещё нет (их не было в мешке А). При этом напротив этих новых названий в столбце для мешка А можно сразу проставить нули.

Главная ошибка при выполнении этой работы — занести в список дважды одну и ту же фигурку (и назвать одну и ту же фигурку разными именами). После того как общий список готов, можно заполнить колонки (таблицы мешков) для А и С. По окончании работы учащиеся не только убеждаются в том, что мешки А и С разные, но и получают алгоритм (способ) для дальнейшей работы. Точно так же можно поступить и с остальными мешками. Составив один общий список всех фигурок, которые встречаются в мешках хотя бы один раз, можно заполнить таблицу для каждого мешка и потом сравнить колонки чисел.

По окончании общего обсуждения каждому учащемуся предлагается самостоятельно поработать со сводной таблицей (с. XXХIХ вкладыша). В первом столбце должен содержаться общий список всех фигурок, встречающихся в мешках. Ребёнок может составить его сразу целиком или по ходу просмотра мешков добавлять названия животных, которые ещё не встречались. На самом деле полный список фигурок появится после просмотра первых трёх мешков (А, В, С). Затем учащийся заполняет таблицу, имея в виду, что таблица каждого мешка — это колонка в сводной таблице, т. е. в столбце под именем каждого мешка.

Ниже приведён один из возможных вариантов заполнения таблицы для четырёх первых мешков.

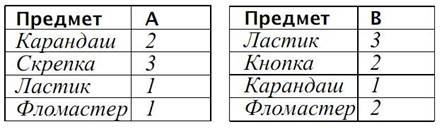
После заполнения всей таблицы (а точнее, таблиц для всех мешков) нужно найти два одинаковых столбца. Можно выявить пару одинаковых столбцов, проглядывая таблицу глазами, но лучше отсортировать таблицы (мы составили мешки так, чтобы, просматривая глазами, найти два одинаковых столбца было трудно). Предложите детям следующий способ: разрезать заполненную большую таблицу на столбцы — отдельные таблицы мешков. Теперь разделим их на кучки с одинаковыми цифрами в первой строке. Затем каждую кучку делим на меньшие кучки, выбирая таблицы с одинаковыми цифрами во втором ряду, и так далее, пока не просмотрим все ряды. Постепенно число кучек будет увеличиваться, а число таблиц в кучках — уменьшаться. Кучки с одной таблицей (одиночные таблицы) можно сразу откладывать в сторону. Возвращаться к ним не придётся. В результате останется одна кучка, содержащая две таблицы. Это и будут таблицы искомых одинаковых мешков.

Второй этап проекта

Для работы понадобятся настоящие мешки (например, полиэтиленовые пакетики) и телесные предметы (детали конструктора «Лего» или разнообразные мелкие канцелярские принадлежности). Мешки надо подготовить заранее по числу учеников, не больше 26 штук (из расчёта один мешок на одного-двух учащихся), не забыв при этом изготовить ровно два одинаковых. Лучше сразу наклеить на каждый мешок имя (букву латинского алфавита). Различных предметов, которые вы положите в эти мешки, должно быть не более 20 — тогда список предметов поместится в заготовленные таблицы.

Каждый учащийся получает свой мешок (пакетик) и составляет таблицу этого мешка (три бланка таких таблиц помещены на с. XVII вкладыша). Для заполнения таблицы ребёнку придётся составить список названий предметов мешка. Можно посоветовать детям вынимать предметы из мешка, одновременно дописывая в левый столбец таблицы названия тех предметов, которые им ещё не встречались. После этого останется подсчитать, сколько раз каждый из предметов встретился в мешке, и заполнить таблицу.

Затем работа ведётся всем классом. Нужно составить один общий список всех предметов, которые есть в мешке хотя бы у одного ученика в классе. Для этого первый ученик выписывает на доске названия всех предметов из своего мешка. Затем второй ученик дописывает названия тех предметов, которые есть в его мешке, но ещё не внесены в список. Все остальные ученики контролируют ход работы.

Продолжает запись следующий ученик. Постепенно в списке оказываются все предметы.

Далее можно организовать два варианта работы: индивидуальный и групповой. В первом случае каждый ученик работает с этой задачей так же, как он работал с задачей 1. Он заполняет сводную таблицу на с. XVIII, разрезает её на отдельные столбцы и находит два одинаковых. Единственное отличие от задачи 1 состоит в том, что у каждого ученика имеется только одна таблица для своего мешка. Чтобы дети могли заполнить сводную таблицу, необходимо организовать обмен информацией. На доске записан общий список предметов. Попросите всех по очереди выйти к доске и выписать столбец для своего мешка. Так каждый ученик сможет заполнить сводную таблицу (переписав с доски) и самостоятельно найти два одинаковых столбца.

Для другого варианта работы — группового — каждый ученик должен заполнить таблицу для своего мешка на с. XVII ещё раз, но уже с новым списком предметов. Перечень и порядок предметов в таблице должны теперь быть в точности такими же, как в общем списке на доске. Напротив названий тех предметов из списка, которых в мешке у учащегося нет, ставится ноль. Далее происходит поиск одинаковых таблиц. При этом если раньше мы делили на кучки столбцы таблицы, то теперь на группы делятся дети. Например, первый ученик говорит: «У меня в первой строчке единица, у кого тоже?» Все дети, у кого в первой строчке 1, подходят к нему. Учитель спрашивает у одного из оставшихся сидеть, какое у него число в первой строчке. Ученик отвечает, и к нему подходят все, у кого в первой строчке такое же число. Образуется несколько довольно больших групп учеников. Каждая из этих групп должна теперь разделиться на несколько подгрупп с одинаковыми числами во второй строке и т. д.

Постепенно групп становится всё больше, а детей в группах всё меньше. В конце концов совпадающие таблицы будут найдены и останется только проверить результат, достав элементы из мешков. Не исключено, что при этом дети обнаружат ошибки.

Ошибки могут быть двух типов:

1. Ученик неправильно составил таблицу мешка.

2. Два разных предмета были названы одинаково. Например, дети считали карандаши, а после проверки оказалось, что у одного карандаш красный, а у другого синий. Скрепки могут оказаться разного размера.

В этом случае необходимо довести работу по сравнению мешков до конца, внеся изменения в таблицы. Обязательно надо обсудить, можно ли было из-за этой ошибки пропустить одинаковые мешки.

Можно организовать и телесное составление таблиц мешков. Для этого понадобится горизонтальная поверхность, на которой следует нарисовать таблицу такого размера, чтобы в любой её клеточке можно было положить все одинаковые элементы одного мешка. Ещё лучше сделать каждый столбец таблицы в виде отдельной картонки, фанерки или полоски лоточков. Такая конструкция таблицы позволит сортировать её столбцы с разложенными на них предметами.

Рассмотрим пример организации работы с телесной таблицей. Сначала каждому мешку присваивается номер или имя (скажем, имя держащего его ученика). Если в классе несколько учеников с одинаковыми именами, то придётся использовать и имя, и фамилию. Затем каждый подписывает один столбец таблицы именем своего мешка. После этого начинается заполнение таблицы элементами мешка. Один ученик достаёт из своего мешка первый попавшийся ему элемент, называет его и кладёт в верхнюю ячейку таблицы. Например: «В верхнюю ячейку таблицы я положу скрепку». Слово «скрепка» записывается на доске, и все ученики, которые находят в своих мешках скрепки, кладут их в свою верхнюю ячейку. Затем тот же или любой другой ученик достает из мешка следующий предмет, называет его и кладет во вторую сверху ячейку. Постепенно все предметы из всех мешков оказываются выложенными в таблицы, причём у всех учеников в одинаковых строчках лежат одинаковые предметы. По завершении первого этапа работы следует приступить к сортировке таблиц, её можно проводить так же, как и описанную выше сортировку обычных таблиц. Во время сортировки иногда выясняется, что при заполнении таблиц разные предметы были названы одинаково. Например, в первую строчку решили поместить карандаши, а когда таблицы положили рядом, выяснилось, что в одном мешке карандаши синие, а в другом — красные. Придётся заполнить в таблице новую строчку, написав в ней, скажем, «карандаши красные», а старую строчку «карандаши» исправить на «карандаши синие».

Выполнив проект, дети получают инструмент нахождения одинаковых мешков, одинаковых массивов, независимо от количества элементов в мешках и числа мешков. Главное — у детей должно остаться ощущение могущества придуманного ими способа решения задачи о нахождении одинаковых мешков; возможно, работа будет долгой, но она обязательно приведёт к результату.

Уроки «Робик. Команды для Робика. Программа для Робика»

На этих уроках дети знакомятся с простым исполни