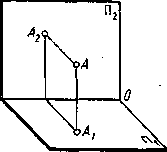
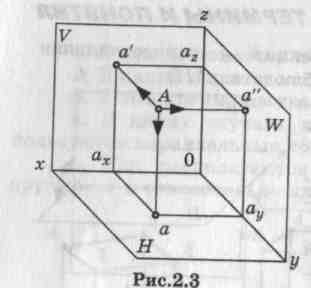
Основные теоретические сведения по теме.

Программой предусмотрено рассмотрение только одного ортогональ­ного (прямоугольного) метода проецирования. Он состоит в том, что все проецирующие лучи параллельны между собой и перпендикулярны плоскости проекций, так называется плоскость, на которую проецируется предмет.

Чтобы получить проекцию А₁ точки А на горизонтальной плоскости (которую будем обозна­чать греческой буквой П—пи), надо из точки А пространства опустить перпендикуляр. Точка пере­сечения перпендикуляра с плоскостью будет проекцией А₁ точки А. '

Плоскость П₁, будем называть горизонтальной плоскостью проекций, а перпендикуляр, опу­щенный из точки А, — проецирующим перпендикуляром. Надо иметь в виду, что если заданы одна плоскость проекций, например П₁, и на ней проекция А₁, то одной проекции недостаточно для того, чтобы определить положение точки в пространстве, так как одна и та же проекция принадлежит множеству точек, расположенных на проецирующем перпендикуляре А₁А (рис. 9).

Следовательно, для определения положения точки А по отношению плоскостей проекций, необходимо задать две проекции А₁ и А₂ точки А (рис. 10), которые начертеже (эпюре) будут расположены на одном перпендикуляре к оси проекций (рис. 11). Та же точка может быть спрое­цирована на три плоскости проекций П₁ П₂ и П₃ (рис. 12).

Прямая линия представляет собой множество точек, и для того чтобы ее спроецировать, достаточно иметь две ее точки.

Прямую, параллельную хотя бы одной из плоскостей проекций, называют прямой част­ного положения.

Прямую, не параллельную и не перпендикулярную ни одной из плоскостей проекций, на­зывают прямой общего положения (рис. 13).

 

 

Рис.10 Рис.12.

 

 

 

Рис. 13

Рис.13

Напомним свойства ортогонального (прямоугольного) метода проецирования:

1. Проекция точки есть точка.

2.Проекция прямой в общем виде всегда прямая (исключение — когда прямая пер- пендикулярна одной из плоскостей проекций).

3. Проекция точки делит проекцию отрезка в том же отношении, в каком точка делит этот отрезок в пространстве.

Надо хорошо знать и понимать взаимное положение прямых в пространстве. Их три: прямые параллельные, пересекающиеся и скрещивающиеся.

Напоминаем, что прямые, параллельные в пространстве, имеют параллельные проекции; прямые, пересекающиеся в пространстве, имеют одну общую точку, проекции которой на чертеже лежат на одном перпендикуляре к оси проекций; если прямые скрещивающиеся, то они не имеют общих точек и не параллельны между собой.

Если прямые в пространстве пересекаются под прямым углом, т. е. перпендикулярны, и если одна из прямых параллельна одной из плоскостей проекций, то прямой угол на эту плос­кость проецируется без искажения, т. е. также в виде прямого угла {рис. 14).

Надо очень хорошо знать, как можно задать плоскость на чертеже — тремя проекциями точек, не лежащих на одной прямой, проекциями двух параллельных прямых, проекциями двух пересекающихся прямых и, наконец, любой плоской фигурой.

Плоскости, как и прямые линии, могут быть общего и частного положения.

Необходимо хорошо усвоить принцип принадлежности (инцидентности).

1. Если прямая принадлежит плоскости, то она должна иметь с этой плоскостью две общие точки 1 и 2 (рис. 15).

2.Если точка Д принадлежит плоскости, то она должна принадлежать прямой А₁ лежащей в этой плоскости (рис. 16).

При проработке материала обратите особое внимание на прямые особого назначения, или главные линии плоскости.

Горизонталь h — прямая, лежащая в плоскости параллельно горизонтальной плоскости проекций (рис. 17). У горизонтали в плоскости общего положения фронтальная проекция параллельна оси проекций ОХ, в плоскости фронтально проецирующей фронтальная проекция горизонтали проецируется в виде точки.

Фронталь f—прямая, линия лежащая в плоскости параллельно фронтальной плоскости проекций (рис. 18). Горизонтальная проекция фронтали в плоскостях общего положения па­раллельная оси ОХ, в плоскости горизонтально-проецирующей (частного положения) горизон­тальная проекция изобразится в виде точки.

Линия наибольшего ската р — это линия, лежащая в плоскости перпендикулярно горизон­талям плоскости. Горизонтальная проекция линии ската перпендикулярна горизонтальной про­екции горизонтали (рис. 19). С помощью этой линии определяют угол наклона данной плоскости к горизонтальной плоскости проекций.

 

 

 

рис.14 рис. 15 рис.16

 

 

 

 

рис.17 рис 18 рис.19

 

Порядок выполнения.

1. Изучить методические указания, ГОСТы и соответствующую литературу.

2. Подготовить рабочее место, инструменты, бумагу и пособия.

3. Ознакомиться с содержанием индивидуального задания и образцом выполнения.

4. Наметить места расположения задания.

5. Построить по координатам точек плоскости α(АВС) и β (DFE).

6. Заключаем одну из сторон, например АС, во фронтально-проецирующую плоскость γ_2.

7. Находим линию пересечения 3-4.

8. Находим горизонтальную проекцию L₁, затем фронтальную проекцию L₂.

9. Сторону заключаем в горизонтально проецирующую плоскость σ_1.

10. Находим линию пересечения 1-2, а затем и точку К (К₁, К₂).

11. Определяем видимость по конкурирующим точкам.

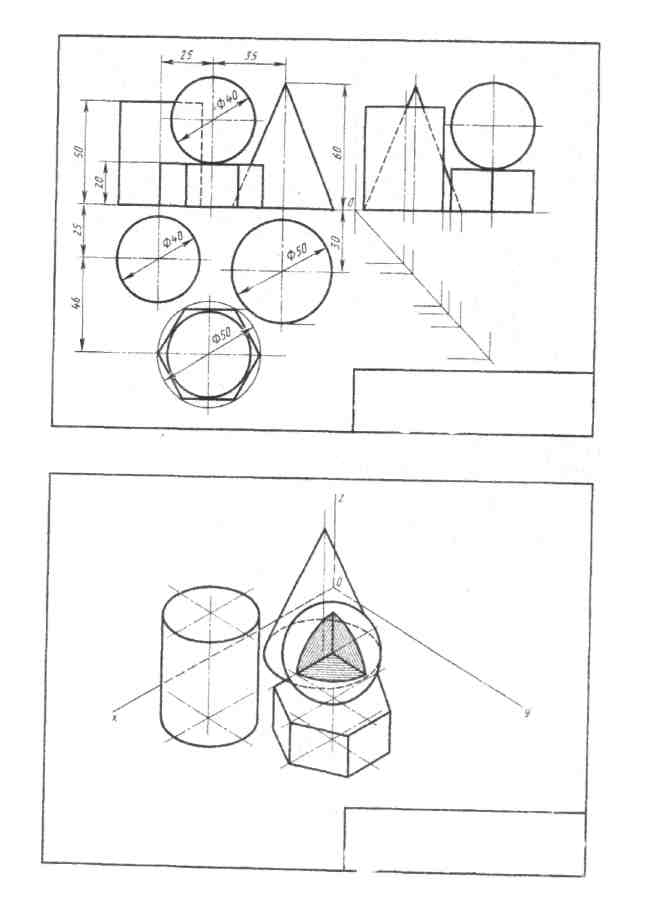
Задание 4

«Проецирование группы геометрических тел.

Аксонометрическое изображение группы геометрическ их тел,»

Цель:

• ознакомиться с сутью метода проецирования.

• научиться выполнять комплексные чертежи геометрических тел.

• научиться выполнять аксонометрические проекции геометрических тел.

Содержание. Вычертить три проекции и аксонометрическое изображение группы геометрических тел на листе чертежной бумаги формата А3(297х420). Образец выполнения дан на рис. 6. Варианты графической работы приведены в таблице 2.