
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет стандартного отклонения для фона контрольной группыСодержание книги
Поиск на нашем сайте
Сумма (Σ) d 2 = 131,94 Варианса (s 2)= Стандартное отклонение (s)= Примечание: Формула для расчетов и сами расчеты приведены здесь лишь в качестве иллюстрации. В наше время гораздо проще приобрести такой карманный микрокалькулятор, в котором подобные расчеты уже заранее запрограммированы, и для расчета стандартного отклонения достаточно лишь ввести данные, а затем нажать клавишу s.
О чем же свидетельствует стандартное отклонение, равное 3,07? Оказывается, оно позволяет сказать, что б о льшая часть результатов (выраженных здесь числом пораженных мишеней) располагается в пределах 3,07 от средней, т. е. между 12,73 (15,8 - 3,07) и 18,87 (15,8 + 3,07). Для того чтобы лучше понять, что подразумевается под «б о льшей частью результатов», нужно сначала рассмотреть те свойства стандартного отклонения, которые проявляются при изучении популяции с нормальным распределением. Статистики показали, что при нормальном распределении «б о льшая часть» результатов, располагающаяся в пределах одного стандартного отклонения по обе стороны от средней, в процентном отношении всегда одна и та же и не зависит от величины стандартного отклонения:она соответствует 68% популяции (т. е. 34% ее элементов располагается слева и 34% — справа от средней):
Точно так же рассчитали, что 94,45% элементов популяции при нормальном распределении не выходит за пределы двух стандартных отклонений от средней:
и что в пределах трех стандартных отклонений умещается почти вся популяция — 99,73 %.
Учитывая, что распределение частот фона контрольной группы довольно близко к нормальному, можно полагать, что 68% членов всей популяции,из которой взята выборка, тоже будет получать сходные результаты, т. е. попадать примерно в 13-19 мишеней из 25. Распределение результатов остальных членов популяции должно выглядеть следующим образом:
Гипотетическая популяция,из которой взята контрольная группа (фон)
Что касается результатов той же группы после воздействия изучаемого фактора, то стандартное отклонение для них оказалось равным 4,25 (пораженных мишеней). Значит, можно предположить, что 68% результатов будут располагаться именно в этом диапазоне отклонений от средней, составляющей 16 мишеней, т. е. в пределах от 11,75 (16 - 4,25) до 20,25 (16 + 4,25), или, округляя, 12-20 мишеней из 25. Видно, что здесь разброс результатов больше, чем в фоне. Эту разницу в разбросе между двумя выборками для контрольной группы можно графически представить следующим образом:
Поскольку стандартное отклонение всегда соответствует одному и тому же проценту результатов, укладывающихся в его пределах вокруг средней, можно утверждать, что при любой форме кривой нормального распределения та доля ее площади, которая ограничена (с обеих сторон) стандартным отклонением, всегда одинакова и соответствует одной и той же доле всей популяции. Это можно проверить на тех наших выборках, для которых распределение близко к нормальному, — на данных о фоне для контрольной и опытной групп. Итак, ознакомившись с описательной статистикой, мы узнали, как можно представить графически и оценить количественно степень разброса данных в том или ином распределении. Тем самым мы смогли понять, чем различаются в нашем опыте распределения для контрольной группы до и после воздействия. Однако можно ли о чем-то судить по этой разнице — отражает ли она действительность или же это просто артефакт, связанный со слишком малым объемом выборки? Тот же вопрос (только еще острее) встает и в отношении экспериментальной группы, подвергнутой воздействию независимой переменной. В этой группе стандартное отклонение для фона и после воздействия тоже различается примерно на 1 (3,14 и 4,04 соответственно). Однако здесь особенно велика разница между средними — 15,2 и 11,3. На основании чего можно было бы утверждать, что эта разность средних действительно достоверна, т. е. достаточно велика, чтобы можно было с уверенностью объяснить ее влиянием независимой переменной, а не простой случайностью? В какой степени можно опираться на эти результаты и распространять их на всю популяцию, из которой взята выборка, т. е. утверждать, что потребление марихуаны и в самом деле обычно ведет к нарушению глазодвигательной координации? На все эти вопросы и пытается дать ответ индуктивная статистика.
Индуктивная статистика
Задачи индуктивной статистики заключаются в том, чтобы определять, насколько вероятно, что две выборки принадлежат к одной популяции. Давайте наложим друг на друга, с одной стороны, две кривые — до и после воздействия — для контрольной группы и, с другой стороны, две аналогичные кривые для опытной группы. При этом масштаб кривых должен быть одинаковым.
Видно, что в контрольной группе разница между средними обоих распределений невелика, и поэтому можно думать, что обе выборки принадлежат к одной и той же популяции. Напротив, в опытной группе большая разность между средними позволяет предположить, что распределения для фона и воздействия относятся к двум различным популяциям, разница между которыми обусловлена тем, что на одну из них повлияла независимая переменная.
Проверка гипотез
Как уже говорилось, задача индуктивной статистики — определять, достаточно ли велика разность между средними двух распределений для того, чтобы можно было объяснить ее действием независимой переменной, а не случайностью, связанной с малым объемом выборки (как, по-видимому, обстоит дело в случае с опытной группой нашего эксперимента). При этом возможны две гипотезы: 1) нулевая гипотеза (H0), согласно которой разница между распределениями недостоверна; предполагается, что различие недостаточно значительно, и поэтому распределения относятся к одной и той же популяции, а независимая переменная не оказывает никакого влияния; 2) альтернативная гипотеза (H1), какой является рабочая гипотеза нашего исследования. В соответствии с этой гипотезой различия между обоими распределениями достаточно значимы и обусловлены влиянием независимой переменной. Основной принцип метода проверки гипотез состоит в том, что выдвигается нулевая гипотеза H0, с тем чтобы попытаться опровергнуть ее и тем самым подтвердить альтернативную гипотезу H1. Действительно, если результаты статистического теста, используемого для анализа разницы между средними, окажутся таковы, что позволят отбросить H0, это будет означать, что верна H1, т. е. выдвинутая рабочая гипотеза подтверждается. В гуманитарных науках принято считать, что нулевую гипотезу можно отвергнуть в пользу альтернативной гипотезы, если по результатам статистического теста вероятность случайного возникновения найденного различия не превышает 5 из 100 [*]. Если же этот уровень достоверности не достигается, считают, что разница вполне может быть случайной и поэтому нельзя отбросить нулевую гипотезу. Для того чтобы судить о том, какова вероятность ошибиться, принимая или отвергая нулевую гипотезу, применяют статистические методы, соответствующие особенностям выборки. [Разумеется, риск ошибиться будет еще меньше, если окажется, что эта вероятность составляет 1 на 100 или, еще лучше, 1 на 1000.] Так, для количественных данных (см. дополнение Б.1) при распределениях, близких к нормальным, используют параметрические методы, основанные на таких показателях, как средняя и стандартное отклонение. В частности, для определения достоверности разницы средних для двух выборок применяют метод Стьюдента, а для того чтобы судить о различиях между тремя или б о льшим числом выборок, — тест F, или дисперсионный анализ. Если же мы имеем дело с неколичественными данными или выборки слишком малы для уверенности в том, что популяции, из которых они взяты, подчиняются нормальному распределению, тогда используют непараметрические методы — критерий χ2(хи -квадрат) для качественных данных и критерии знаков, рангов, Манна—Уитни, Вилкоксона и др. для порядковых данных. Кроме того, выбор статистического метода зависит от того, являются ли те выборки, средние которых сравниваются, независимыми (т. е., например, взятыми из двух разных групп испытуемых) или зависимыми (т. е. отражающими результаты одной и той же группы испытуемых до и после воздействия или после двух различных воздействий).
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 304; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.163.23 (0.01 с.) |

 =
= 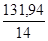 = 9,42.
= 9,42. =
=  = 3,07.
= 3,07.









