Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Упражнение 5. Решение системы линейных уравнений Методом КрамераСодержание книги
Поиск на нашем сайте Дана линейная система По методу Крамера Например, нужно решить систему линейных уравнений с 3 неизвестными, с коэффициентами 1. Вводим матрицы A, b, затем копируем матрицу A три раза (начальная заготовка для матрицы
Рис. 1 2. Затем копируем столбец b и вставляем его в А1 в 1 столбец, в А2 во 2 столбец, в А3 - в 3 столбец 3. Вычислите определители полученных матриц в ячейки Н7, Н11, Н15. 4. После определения определителей матриц А1, А2, А3 легко можно получить Х1 по формуле Задания для самостоятельной работы: 1. Решить системы линейных уравнений а) Методом Крамера 2. Вычислите б) квадратичную форму
Таблица 1.
3. Найдите значение сложных выражений Таблица 2.
Контрольные вопросы: 1. Что значит транспонировать матрицу? 2. С помощью каких функций сумм вычисляются сложные выражения? 3. В чем заключается метод Крамера? 4. При каком условии система линейных уравнений имеет решение? 5. Что выполняет функция СУММКВ?
Лабораторная работа №14 Тема: «Поиск решения и решение оптимизационных задач. Линейная оптимизационная задача. Планирования производства красок» Цель работы: сформировать умение решать линейные оптимизационные задачи. Основные понятия: Поиск решения (Solver) – это единый, мощный инструмент решения оптимизационных задач. Упражнение 1. Задача об оптимальном производстве красок. Небольшая фабрика выпускает два типа красок: для внутренних (I) и наружных работ (E). Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта А и В. Максимально возможные суточные запасы этих продуктов составляет 6 т и 8 т соответственно. Расходы А и В на 1 т соответствующих красок приведены в таблице 1. Таблица 1.
Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает спроса на краску E более чем на 1 т. Кроме того, установлено, что спрос на краску I никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3 000 руб. для краски E и 2 000 руб. для краски I. Какое количество краски каждого вида фабрика, чтобы доход от реализации продукции был максимальным? 1.1. Для решения этой задачи необходимо сначала построить математическую модель: 1. Для определения каких величин строится модель? Что является переменными модели? 2. В чем состоит цель, для достижения которой из множества всех допустимых значений переменных выбираются оптимальные? 3. каким ограничениям должны удовлетворять неизвестные? В нашем случае фабрике необходимо спланировать объем производства красок так, чтобы максимизировать прибыль. Поэтому переменными являются
Суммарная суточная прибыль от производства хI краски I и хЕ краски E равна Целью фабрики является определение среди всех допустимых значений Кроме того ограничения на величину спроса на краски таковы: Таким образом. Математическая модель данной задачи имеет следующий вид: Максимизировать
Заметим, что данная модель является линейной, т.к. целевая функция и ограничения линейно зависят от переменных.
1.2. Введите данные как в таблице 2. Отведем ячейки А3 и В3 под значения переменных Таблица 2.
1.3. Теперь нажмите кнопку Параметры в диалоговом окне Поиск решения, для того чтобы проверить, какие параметры заданы для поиска решений. 1.4. Запишите в тетради условие задачи, алгоритм нахождения решений и сделайте соответствующий вывод. Задания для самостоятельной работы: Вариант 1. Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линий 75 изделий. На радиоприемник первой модели расходуется 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй модели равна $30 и $20 соответственно. Определить оптимальный суточный объем производства первой и второй модели. Вариант 2. Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Время использования этих станков для производства данных изделий ограничено 10 ч в сутки. Найти оптимальный объем производства изделий каждого вида.
Вариант 3. Фирма имеет возможность рекламировать свою продукцию, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.
Вариант 4. Автозавод выпускает автомобили четырех видов: W,X,Y,Z (Хат, Седан, Джип, Вагон). Ежемесячно он может выпускать не более 1000 автомобилей (при этом каждого типа – не меньше 100). В течение месяца 1000 работников завода работают по 150 часов каждый. Завод может израсходовать за месяц не более 900 тонн стали.
Контрольные вопросы: 1. Какое средство Excel используется для решения линейных оптимизационных задач? 2. Каким образом записываются ограничения? 3. Что такое целевая функция? 4. Что такое математическая модель? 5. Как вы понимаете переменные модели?
Лабораторная работа №15
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.01 с.) |

 , где
, где  – матрица коэффициентов,
– матрица коэффициентов,  – столбец (вектор) свободных членов,
– столбец (вектор) свободных членов,  – столбец (вектор) неизвестных.
– столбец (вектор) неизвестных. вычисляется по формуле
вычисляется по формуле  , где
, где  - определители матрицы
- определители матрицы  ,
,  - определитель исходной матрицы т.е матрицы А.
- определитель исходной матрицы т.е матрицы А.  и с правой частью
и с правой частью  .
. , и так для Х2, Х3
, и так для Х2, Х3 .
.
 б)
б) 



 б)
б) 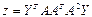

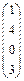

 б)
б) 









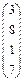
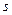 , где а, x, y – вектор из n компонентов,
, где а, x, y – вектор из n компонентов, 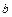 и
и  – матрица размерности
– матрица размерности  .
. ,
, 















 – суточный объем производства краски I;
– суточный объем производства краски I;  – суточный объем производства краски E.
– суточный объем производства краски E. .
. . Перейдем к ограничениям, которые налагаются на
. Перейдем к ограничениям, которые налагаются на  . Расход исходного продукта для производства обоих видов красок не может превосходить максимально возможный запас данного исходного продукта. Следовательно:
. Расход исходного продукта для производства обоих видов красок не может превосходить максимально возможный запас данного исходного продукта. Следовательно: 

 при следующих ограничениях:
при следующих ограничениях:
 1.3. Выберите команду Сервис/Поиск решения. Если отсутствует команда Поиск решения, то для ее установки необходимо выполнить команду Сервис/Надстройки/Поиск решения. В открывшемся диалоговом окне, в поле Установить целевую ячейку сделайте ссылку на ячейку С4, включите Равной Максимальному значению, введите в поле Значению 0, в поле Изменяя ячейки укажите диапазон ячеек А3:В3. Переходите в поле Ограничения и нажмите кнопку Добавить и в следующем диалоговом окне Добавления ограничения введите ограничения:
1.3. Выберите команду Сервис/Поиск решения. Если отсутствует команда Поиск решения, то для ее установки необходимо выполнить команду Сервис/Надстройки/Поиск решения. В открывшемся диалоговом окне, в поле Установить целевую ячейку сделайте ссылку на ячейку С4, включите Равной Максимальному значению, введите в поле Значению 0, в поле Изменяя ячейки укажите диапазон ячеек А3:В3. Переходите в поле Ограничения и нажмите кнопку Добавить и в следующем диалоговом окне Добавления ограничения введите ограничения: