Определение жесткостей элементов рамы

Длину стоек, вводимых в расчет, принимаем равной высоте этажа h_эт=3.3 м.

Средняя расчетная длина ригелей:

l₀=(l₀₁+l₀₂)/2=(6200+6400)/2=6300 мм=6.3 м.

Расстояние от центра тяжести сечения до нижней грани сечения ригеля:

y=S/A_p=0.090/0.286=0.3147 м, где A_p=b_p*h_p=0.3*0.7=0.286 м².

S=b_p*h_p²/2+2*0,02*h_пл*0,5*(h_p-h_пл+h_пл/3)+2*0,17*0,1*(h_p-h_пл-0,05)+2*0,17*(h_p-h_пл-0,1)²*0,5*2/3=0.3*0.7²/2+2*0,02*0.4*0,5*(0.7-0.4+0.4/3)+2*0,17*0,1*(0.7-0.4-0,05)+2*0,17*(0.7-0.4-0,1)²*0,5*2/3=0.090 м³ – статический момент относительно нижней грани сечения.

Определим жесткости ригеля (1), средних стоек (2) и крайних стоек (3), а также их соотношения.

1) Момент инерции сечения ригеля относительно центра тяжести:

I_p=b_p*h_p³/12+b_p*h_p*(h_p/2-y)²=0.3*0.7³/12+0.3*0.7*(0.7/2-0.3147)²=0.00884 м⁴.

Погонная жесткость ригеля (ригель из бетона класса B25, бетон подвергнут тепловой обработке, E_b=27000 МПа):

i_p=E_b*I_p/l₀=27*10³*0.00884/6.3=37872 кН*м.

2) Момент инерции сечения средней стойки:

I^ср_s3=b^ср_col*h^ср_col³/12=0.4*0.6³/12=0.0072 м⁴.

Погонная жесткость средних стоек (колонна из бетона класса B30, бетон подвергнут тепловой обработке E_b=29000 МПа):

i_3s=i’_3s=E_b*I^ср_s3/h_эт=29000*10³*0.0072/3.3=63273 кН*м.

Соотношение жесткостей:

η₃=(i_3s+1,5*i’_3s)/i_p=(63273+1,5*63273)/37872=4.177.

3) Момент инерции сечения крайней стойки:

I^кр_s4=b^кр_col*h^кр_col³/12=0.4*0.4³/12=0.00213 м⁴.

Погонная жесткость крайних стоек (колонна из бетона класса B30, бетон подвергнут тепловой обработке E_b=29000 МПа):

i_4s=i’_4s=E_b*I^кр_s4/h_эт=29000*10³*0.00213/3.3=18747 кН*м.

Соотношение жесткостей:

η₄=(i_4s+1,5*i’_4s)/i_p=(18747+1,5*18747)/37872=1.238.

Расчетная схема и статический расчет поперечной рамы

Расчетная схема поперечной рамы изображена на рис. 2.3.

Рис. 2.3. Расчетная схема поперечной рамы.

Статический расчет поперечной рамы проведем в программе RAMA2. Исходные данные для выполнения расчета сведены в таблицу 2.

Таблица 2.

Исходные данные для программы RAMA2.

Величина	l01	l02	Pg^пер	PV^пер	η3	η4
Обозначение в программе	L01	L02	Pgпер	Pvпер	K1	K2
Значение	6.2000	6.4000	30,6830	94.5400	4.1770	1.2380

╔═══════════════════════════════════════════════════════════════════════╗

║ Исходные данные ║

╠═══════════╦═══════════╦═══════════╦═══════════╦═══════════╦═══════════╣

║ L01 ║ L02 ║ Pgper ║ Pvper ║ K1 ║ K2 ║

║ [м] ║ [м] ║ [кН/м] ║ [кН/м] ║ ║ ║

╠═══════════╬═══════════╬═══════════╬═══════════╬═══════════╬═══════════╣

║ 6.2000║ 6.4000║ 30.6830║ 94.5400║ 4.1770║ 1.2380║

╚═══════════╩═══════════╩═══════════╩═══════════╩═══════════╩═══════════╝

 

╔═════════════════════════════════════════════════════════════════════╗

║ Изгибающие моменты в ригеле [кН/м] ║

╠═════╦═══════╦═══════╦═══════╦═══════╦═══════╦═══════╦═══════╦═══════╣

║ ║ M A ║ M1 ║ M2 ║ M3 ║ M BL ║ M BP ║ M4 ║ M5 ║

╠═════╬═══════╬═══════╬═══════╬═══════╬═══════╬═══════╬═══════╬═══════╣

║ 1+2 ║-370.04║ 84.93║ 239.04║ 92.31║-355.27║-195.84║ -78.01║ -38.74║

╠═════╬═══════╬═══════╬═══════╬═══════╬═══════╬═══════╬═══════╬═══════╣

║ 1+3 ║ -57.79║ 12.03║ 8.15║ -69.46║-220.78║-386.36║ 94.49║ 254.78║

╠═════╬═══════╬═══════╬═══════╬═══════╬═══════╬═══════╬═══════╬═══════╣

║ 1+4 ║-307.31║ 95.20║ 196.87║ -2.31║-502.35║-497.22║ -16.36║ 143.93║

╚═════╩═══════╩═══════╩═══════╩═══════╩═══════╩═══════╩═══════╩═══════╝

 

╔═══════════════════════════════════════════════════════╗

║ Поперечные силы в ригеле [кН] ║

╠═════════════╦═════════════╦═════════════╦═════════════╣

║ Q A ║ Q BL ║ Q BP ║ Q CL ║

╠═════════════╬═════════════╬═════════════╬═════════════╣

║ 390.5728║ -385.8098║ 98.1856║ -98.1856║

╠═════════════╬═════════════╬═════════════╬═════════════╣

║ 68.8292║ -121.4054║ 400.7136║ -400.7136║

╠═════════════╬═════════════╬═════════════╬═════════════╣

║ 356.7342║ -356.7342║ 400.7136║ -400.7136║

╚═════════════╩═════════════╩═════════════╩═════════════╝

 

╔═══════════════════════════════════════════════════════════════════════╗

║ Изгибающие моменты в колоннах [кН/м] ║

╠═════╦══════════╦══════════╦══════════╦══════════╦══════════╦══════════╣

║ ║ M AB ║ M AH ║ M A0 ║ M BB ║ M BH ║ M B0 ║

╠═════╬══════════╬══════════╬══════════╬══════════╬══════════╬══════════╣

║ 1+2 ║ 148.0145║ -222.0217║ 111.0108║ -63.7738║ 95.6606║ -47.8303║

╠═════╬══════════╬══════════╬══════════╬══════════╬══════════╬══════════╣

║ 1+3 ║ 23.1171║ -34.6757║ 17.3379║ 66.2340║ -99.3509║ 49.6755║

╠═════╬══════════╬══════════╬══════════╬══════════╬══════════╬══════════╣

║ 1+4 ║ 122.9247║ -184.3871║ 92.1936║ -2.0516║ 3.0774║ -1.5387║

╚═════╩══════════╩══════════╩══════════╩══════════╩══════════╩══════════╝

 

Способ выравнивания – Луговой

 

 

╔══════════════════════════════════════════════════╗

║ Выравненные изгибающие моменты в ригеле [кН/м] ║

╠═════╦════════╦════════╦════════╦════════╦════════╣

║ ║ M A ║ M2 ║ M BL ║ M BP ║ M5 ║

╠═════╬════════╬════════╬════════╬════════╬════════╣

║ 1+2 ║ -370.04║ 239.04║ -355.27║ -195.84║ -38.74║

╠═════╬════════╬════════╬════════╬════════╬════════╣

║ 1+3 ║ -57.79║ 8.15║ -220.78║ -386.36║ 254.78║

╠═════╬════════╬════════╬════════╬════════╬════════╣

║ 1+4 ║ -307.31║ 254.86║ -386.36║ -386.36║ 199.35║

╚═════╩════════╩════════╩════════╩════════╩════════╝

Перераспределение усилий, построение огибающих эпюр

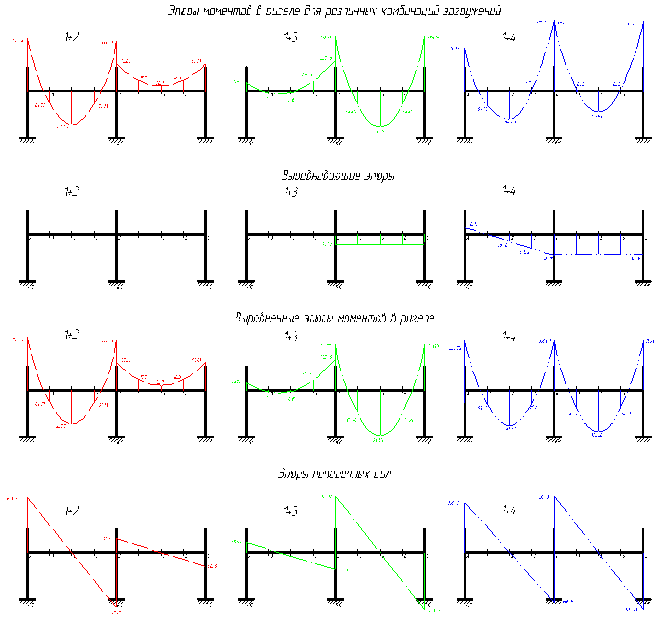
Рис. 2.4. Эпюры изгибающих моментов и поперечных сил в упругой стадии для различных комбинаций загружения ригелей.

Выравнивание для сочетания нагрузок 1+2.

1) Условия M_BL>M_A, M_BL>M₂ не выполняются, перераспределение невозможно.

Выравнивание для сочетания нагрузок 1+3.

1) ∆М=0.5*(M_BP-М₅)=0.5*(368.36-254.78)=56.79 кН*м.

2) 0,3*M_BP=0,3*368.36=110.508 кН*м.

3) Принимаем ∆М=56.79 кН*м.

Выравнивание для сочетания нагрузок 1+4.

Максимальный момент в М_max=502.35 кН*м первом пролете.

Перераспределение начнем с первого пролета:

1) ∆М=0.75*(502.35-307.31)=146.28 кН*м.

2) 0,3*М_max=0,3*502.35=150.705 кН*м.

3) Принимаем в первом пролете ∆М=146.28 кН*м.

4) Принимаем во втором пролете ∆М=141.15 кН*м.

Рис. 2.5. Огибающие эпюры.