
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тест «Теоремы сложения и умножения вероятностей»Содержание книги
Поиск на нашем сайте
1. Отметьте два правильных ответа. Если события A и B независимы, то: 1) 3)
2. Вероятность произведения Не равна 0, Любому числу от 0 до 1, 4) 1
3. Вероятность произведения 1) 3)
4. Отметьте два правильных ответа. Вероятность произведения 1) 3)
5. Вероятность произведения двух несовместных событий 1) 0, 2) 3) 1, 4) 6. Вероятность совместного наступления двух независимых событий 1) 3) 7. Вероятность суммы противоположных событий 1) 1, 2) 0, 3) 8. Вероятность противоположного события 1) 3) 0, 4) 9. Если из урны, содержащей 2 белых и 3 черных шара, берут последовательно с возвращением 2 шара, то вероятность появления первого белого и второго черного шара равна: 1) 3) Тест «Условная вероятность» 1. Если из урны, содержащей 2 белых и 3 черных шара, берут последовательно без возвращения 2 шара, то вероятность появления первого белого и второго черного шара равна: 1) 2. Студент знает 15 из 20 вопросов программы. Вероятность того, что студент знает предложенные ему экзаменатором три вопроса, равна: 1) 3) 3. В группе студентов, состоящей из 15 девушек и 10 юношей, выбираются староста и профорг группы. Вероятность того, что выберут двух юношей, равна: 1) 3) 4. В группе студентов, состоящей из 15 девушек и 10 юношей, выбираются староста и профорг группы. Вероятность того, что выберут одну девушку и одного юношу, равна: 1) 3)
Тест «Формула Бернулли» 1. Отметьте два правильных ответа. Вероятность 1) 3)
2. Установите в схеме независимых испытаний Бернулли соответствие между событиями
и вероятностями 1) 3. Установите в схеме независимых испытаний Бернулли соответствие между биномиальными вероятностями 1) и формулами для их вычисления. А)
4. Отметьте два правильных ответа. Вероятность того, что при четырех подбрасываниях монеты герб появится четыре раза, равна:
1)
5. Отметьте два правильных ответа. Вероятность того, что при четырех подбрасываниях монеты герб появится хотя бы один раз, равна: 1) 4)
6. Наивероятнейшее число Или 2, 4) 2 или 3
7. Вероятность 1) 2) 3)
8. Вероятность 1) 3)
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 993; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.153.218 (0.009 с.) |

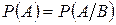 , 2)
, 2)  ,
,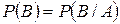 , 4)
, 4) 
 двух несовместных событий A и B равна:
двух несовместных событий A и B равна: , 2)
, 2)  ,
,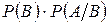 , 4) 0
, 4) 0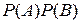 ,
,
 и
и  равна:
равна: 2)
2) 
 4)
4) 
 равна:
равна: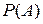 , 4)
, 4) 
 , 2)
, 2)  ,
,
 , 2)
, 2)  ,
, , 4)
, 4) 
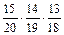 , 2)
, 2)  ,
, , 4)
, 4) 
 , 2)
, 2)  ,
, , 4)
, 4) 
 , 2)
, 2)  ,
, , 4)
, 4) 
 того, что в схеме
того, что в схеме  независимых испытаний событие
независимых испытаний событие  наступит
наступит  раз, равна:
раз, равна: , 2)
, 2) 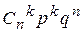 ,
, , 4)
, 4) 
 , 2)
, 2)  , 3)
, 3) 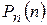 , 5)
, 5)  .
. , Б)
, Б)  , В)
, В)  , Г)
, Г)  , Д)
, Д)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  ,
, , 2)
, 2)  ,
,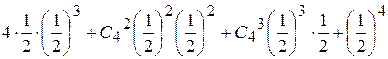 .
. появления герба при четырех подбрасываниях монеты равно:
появления герба при четырех подбрасываниях монеты равно: при
при  находится по формуле:
находится по формуле: ,
, ,
,
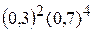
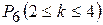 при
при  , 2)
, 2)  .
.


