
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Первая, 2) вторая, 3) обе несовместны, 4) обе совместны.Содержание книги
Поиск на нашем сайте
4. Найти определитель системы уравнений 1) 2, 2) -5, 3) 5, 4) 0. 5. Зная значения Система несовместна, 4) -5, 5) -1. 6. Какие из наборов значений неизвестных 1) 7. Какие наборы значений неизвестных 1) 8. Совместна и определенна ли система уравнений Совместна и определенна, 2) совместна и неопределенна, Несовместна, 4) несовместна и определенна.
9. Система линейных уравнений 1) имеет бесконечное множество решений 2) не имеет решений 3) имеет два решения 4) имеет единственное решение 10. Если 1) 1 2) – 1 3) 2 4) – 2
Тест «Векторы» 1. Даны точки 1) 3. Дан вектор 1) 14, 2) -6, 3) -2, 4) -4, 5) 6. 4. Даны векторы 1) 0, 2) -1, 3) 1, 4) 2, 5) -2. 5. Найти скалярное произведение 6. Даны векторы 1) 7. Для каких значений 1) 12, 2) 6, 3) 8. Какие условия выполняются для коллинеарных векторов 1) 9. Чему равно скалярное произведение 10. Даны два вектора: 1) 9 2)
ТЕСТ «Прямые» 1. Какие из данных уравнений задают на плоскости прямые: ( 1) Все уравнения, 5) другой ответ. 2. Выяснить без построения, какие из данных прямых параллельны: ( 1) 4) 3. Какие из данных прямых перпендикулярны: ( 1) 4. Две прямые 1) 3) 5. Каковы знаки для 1) 3) 6. В уравнении прямой линии Проходит через начало координат, 2) параллельна оси ОХ, Параллельна оси ОУ, 4) образует с осью ОХ острый угол,
Образует с осью ОУ тупой угол 7. В общем уравнении прямой Проходит через начало координат, 2) параллельна оси ОХ, Параллельна оси ОУ, 4) совпадает с осью ОХ, Является осью ОУ 8. Найдите для прямой 1) 9. Найдите для прямой 1) 10. Дано неравенство Да, нет, 2) нет, да, 3) да, да, 4) нет, нет 11. Угловой коэффициент прямой, заданной уравнением 12. Угловой коэффициент прямой, заданной уравнением 1) 13. Прямая линия проходит через точки 1)
Тест «Кривые второго порядка»
1. Какие из заданных уравнений определяют эллипсы: а) А, в, 2) б, г, 3) а, г, 4) а, в, г, 5) а, б, г. 2. Найдите координаты вершины параболы 1) 3. Найдите координаты вершины параболы 1) 4. Каковы координаты центра окружности 1) 5. Найдите параметры 1) 4 и 2, 2) 2 и 1, 3) 2 и 6. Запишите уравнения асимптот гиперболы 1) 7. Найдите точку пересечения линии 1) 8. Найдите точки пересечения линии 1) 9. Укажите соответствие между уравнениями и видами кривых второго порядка a) парабола, b) эллипс, с) гипербола, d) окружность 10. Если уравнение окружности имеет вид 1) 11. Расстояние между фокусами эллипса 12. Уравнением кривой второго порядка
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 522; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.181.225 (0.007 с.) |

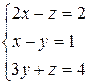 .
. и
и  , найти значение
, найти значение  , удовлетворяющее системе уравнений
, удовлетворяющее системе уравнений  .
. ,
,  являются решением системы
являются решением системы  ?
? , 2)
, 2)  , 3)
, 3) 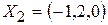 являются решением системы
являются решением системы  ?
? …
… и
и 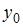 являются решением системы линейных уравнений
являются решением системы линейных уравнений 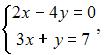 то их разность
то их разность  равна …
равна … ,
,  . Найти координаты вектора
. Найти координаты вектора  .
. 2)
2)  , 3)
, 3) 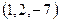 , 4)
, 4)  , 5)
, 5)  .
. . Найти его длину.
. Найти его длину. ,
,  . Найти скалярное произведение
. Найти скалярное произведение  .
. , если длины векторов
, если длины векторов  , а угол между ними равен
, а угол между ними равен  . 1)
. 1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4) 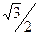 , 5)
, 5)  .
. ,
,  ,
,  . Какие из них коллинеарны?
. Какие из них коллинеарны? и
и  , 2)
, 2)  , 3)
, 3) 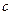 векторы
векторы  и
и  ортогональны?
ортогональны?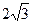 , 4) 4
, 4) 4 ?
? , 2)
, 2)  , 3)
, 3) 
 , если вектор
, если вектор 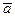 перпендикулярен
перпендикулярен  ? 1)
? 1) 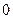 , 2)
, 2)  , 3)
, 3) 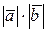
 и
и 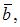 где
где 
 угол между векторами
угол между векторами 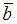 равен
равен  Тогда скалярное произведение векторов
Тогда скалярное произведение векторов 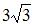 3) 6 4)
3) 6 4) 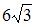
 )
) 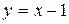 , (
, ( )
)  , (
, (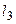 )
)  ?
?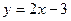 , (
, (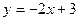 , (
, (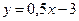 , (
, (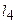 )
) 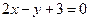 , (
, (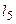 )
) 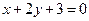 .
.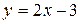 , (
, (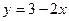 , (
, (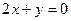 .
.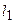 ,
, 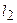 , 2)
, 2) 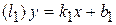 и
и 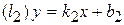 параллельны. Какие условия справедливы?
параллельны. Какие условия справедливы?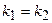 ,
, 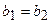 , 2)
, 2) 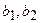 - любые,
- любые,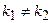 ,
, 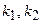 - любые.
- любые.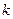 и
и  , если прямая
, если прямая 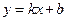 образует с осью абсцисс острый угол?
образует с осью абсцисс острый угол?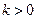 ,
, 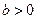 , 2)
, 2) 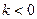 ,
, 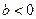 , 4)
, 4)  коэффициенты
коэффициенты 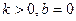 . Как располагается прямая?
. Как располагается прямая? коэффициенты
коэффициенты 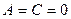 . Как располагается прямая?
. Как располагается прямая? , 2)
, 2) 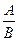 , 3)
, 3)  , 4)
, 4) 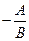 , 5)
, 5) 
 угловой коэффициент.
угловой коэффициент. , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  , 5)
, 5)  , задающее полуплоскость. Содержит ли полуплоскость точки
, задающее полуплоскость. Содержит ли полуплоскость точки  и (1,-2)?
и (1,-2)?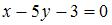 , равен …
, равен … , равен …
, равен …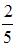 2)
2) 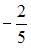 3)
3) 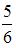 4)
4) 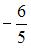
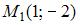 и
и 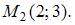 Тогда она пересекает ось Ox в точке …
Тогда она пересекает ось Ox в точке …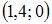 2)
2) 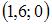 3)
3)  4)
4) 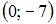
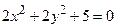 , б)
, б) 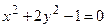 , в)
, в) 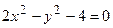 , г)
, г) 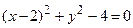 .
. .
. , 2)
, 2) 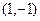 , 3)
, 3)  , 4)
, 4)  , 5)
, 5)  .
.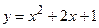 .
. , 2)
, 2)  , 4)
, 4)  , 5)
, 5)  .
.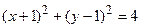 ?
?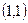 , 2)
, 2)  , 3)
, 3)  , 4)
, 4) 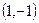 .
. и
и  .
. , 4)
, 4)  и
и  .
. .
.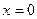 , 2)
, 2)  , 3)
, 3)  , 4)
, 4) 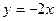 .
. с осью абсцисс.
с осью абсцисс.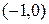 , 2)
, 2)  , 3)
, 3)  с осью ординат.
с осью ординат.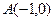 , 2)
, 2)  , 2.
, 2.  , 3.
, 3. 
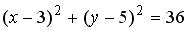 , то его центром
, то его центром  и радиусом
и радиусом 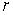 являются …
являются … ,
, 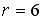 , 2)
, 2)  ,
,  , 4)
, 4)  равно … (запишите ответ).
равно … (запишите ответ).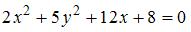 на плоскости определяется …
на плоскости определяется …


