Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Темы заданий для курсовой работыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
МЕХАНИКА Методические указания к выполнению курсовой работы
Мурманск УДК 531 ББК 30.121 М 55
Составитель – Инна Анатольевна Курносова, доцент кафедры технической механики Мурманского государственного технического университета
Методические указания рассмотрены и одобрены кафедрой 19 мая
Рецензент – И. В. Ходяков, канд. техн. наук, профессор кафедры технической механики Мурманского государственного технического университета
Редактор Т. В. Анисимова Корректор Т. А. Пехтерева Электронная верстка Г. М. Плишко
© Мурманский государственный © И. А. Курносова, 2011 ОГЛАВЛЕНИЕ ВВЕДЕНИЕ.. 4 ОБЩИЕ УКАЗАНИЯ К ВЫБОРУ ВАРИАНТОВ ЗАДАНИЙ.. 4 ТЕМЫ ЗАДАНИЙ ДЛЯ КУРСОВОЙ РАБОТЫ... 6 1. Растяжение, сжатие. 6 2. Расчет неразъемного соединения (шов котла) 12 3. Геометрические характеристики плоских сечений.. 18 4. Кручение. 27 5. Напряжения при изгибе. 35 6. Деформации при изгибе. 46 7. Сложное сопротивление. Изгиб с кручением.. 49 ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА.. 63 ПРИЛОЖЕНИЯ.. 64 Приложение 1. Ориентировочные величины основных Приложение 2. Модули упругости.. 64 Приложение 3. Пределы текучести некоторых сталей.. 64 Приложение 4. Рекомендуемые значения основных параметров Приложение 5. Значения предела текучести Приложение 6. Геометрические характеристики плоских сечений.. 66 Приложение 7. Сортамент прокатной стали. 67 Приложение 8. Швеллеры.. 68 Приложение 9. Уголки неравнобокие. 69 Приложение 10. Нормальные линейные размеры.. 73 Приложение 11. Образец оформления титульного листа. 74 Приложение 12. Основная надпись для текстовых документов. 75 Приложение 13. Первый (начальный) лист каждого задания. 75 Приложение 14. Основная надпись для текстовых документов Приложение 15. Основная надпись для чертежей и схем.. 76
ВВЕДЕНИЕ Настоящие методические указания разработаны в соответствии с Государственным образовательным стандартом высшего профессионального образования, учебным планом и рабочей программой дисциплины "Механика" для специальности 140106.65 "Энергообеспечение предприятий". Основная цель выполнения курсовой работы (КР), предусмотренной учебным планом, заключается в выработке навыков и умений для применения теоретических положений при решении инженерных задач. Курс "Механика" включает в себя весьма обширный круг проблем. Автор ограничился освещением только тех вопросов, которые непосредственно связаны с выполнением курсовой работы. Темы заданий КР являются базовыми для изучения последующих Методические указания содержат основные теоретические сведения по темам курсовой работы, расчетные схемы, варианты заданий, примеры решения типовых схем, а также требования, предъявляемые к оформлению курсовой работы. В конце методических указаний приведены приложения с выдержками из литературы и образцы оформления листов пояснительной записки. Так как основные разделы курса "Механика" являются базовыми для многих специальных дисциплин при подготовке инженеров по различным специальностям, то данные методические указания могут быть использованы студентами и курсантами других специальностей для самостоятельной работы по отдельным темам. ОБЩИЕ УКАЗАНИЯ К ВЫБОРУ ВАРИАНТОВ ЗАДАНИЙ Каждое задание к курсовой работе включает таблицу и рисунки, Для определения варианта задания в качестве учебного шифра необходимо использовать номер студенческого билета или шифр, который укажет преподаватель. Исходные данные к задачам выбирают по прилагаемым таблицам Например: шифр 9 8 0 4 6 буквы а б в г д Из столбцов таблицы, обозначенных внизу буквами, нужно выбрать значение, стоящее в строке, номер которой соответствует цифре шифра, расположенной над буквой. Например, для номера 98046 из столбца, обозначенного буквой "д", выбирается значение, стоящее в строке под номером 6: F = 400 кН (см. фрагмент таблицы). Фрагмент таблицы
Четность или нечетность номера определяется по последней цифре шифра. Например, шифр 98046 – четный вариант. По выбранным данным студент формирует схему конкретной задачи. Для всех расчетных схем принято вдоль бруса располагать ось Z, а в плоскости поперечного сечения – оси X и Y. В таблице знак "+" для нагрузок означает, что направление силовых факторов на сформированной схеме должно быть таким же, как на исходном рисунке. Знак "–" означает направление, противоположное указанному на исходном рисунке. Если в таблице исходных данных к задаче какой-либо силовой фактор равен нулю, то на сформированной схеме он будет отсутствовать. Например, q 2 = 0 означает, что на втором участке сформированной схемы отсутствует распределенная нагрузка. Для отдельных заданий предусмотрены дополнительные указания к выбору схемы и варианта. Эти указания помещены непосредственно в темах заданий. Растяжение, сжатие Пример расчета Расчет выполнен для стержня, показанного на рис. 1.4. Материал части стержня с площадью поперечного сечения А – сталь, части с площадью поперечного сечения 2 А – чугун.
Рис. 1.4
При построении эпюры продольной силы необходимо разделить стержень на участки. В данном случае таких участков три. Определение продольных сил рекомендуется начинать со свободного конца стержня. I участок: 0 £ z £ 0,6 м. N 1 = – F 1 = –10 кН (const). II участок: 0,6 м £ z £ 1 м. N 2 = – F 1 – F 2 + q (z 2 – 0,6). При z 2 = 0,6 м N 2 = – F 1 – F 2 = –10 – 15 = –25 кН; при z 2 = 1,0 м N 2 = – F 1 – F 2 + q × 0,4 = –10 – 15 + 5 × 0,4 = –23 кН. III участок: 1 м £ z £ 1,5 м. N 3 = – F 1 – F 2 + q × 0,4 + F 3 = –10 – 15 + 5 × 0,4 + 40 = 17 кН. На рис. 1.5 представлены сечения стержня и эпюра продольной силы.
Рис. 1.5 При определении размеров поперечного сечения стержня необходимо воспользоваться условиями прочности: для стали для чугуна
где
Значения допускаемых напряжений для стали и чугуна приведены Рассмотрим напряжения на участках. I участок (сталь, сжатие):
II участок (чугун, сжатие):
III участок (чугун, растяжение):
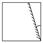
Принято: А = 1,32 × 10–4 м2. В зависимости от формы поперечного сечения стержня можно вычислить его размеры (d; а). Перемещение свободного конца стержня D l = –D l 1 – D l 2 + D l 3. Перемещения каждого участка стержня определяются по формулам (1.2), (1.3):
Стержень стал короче на 2,62×10–4 м.
2. Расчет неразъемного соединения (шов котла) Задание 2. Рассчитать продольный прочноплотный шов для котла с внутренним давлением q, диаметром D, выполненного из стали (выбрать марку стали по табл. 2.1), а также определить напряжения на наклонной площадке элемента стенки котла. Данные взять из табл. 2.1 в соответствии с номером, указанным преподавателем.
Указания к выполнению задания 2 1. Условие прочности на растяжение для тонкостенного сосуда имеет вид
В зависимости от температуры нагрева стенки сосуда (котла) рассчитать [sp]: – при температуре t < 250 °С
где n пч – коэффициент запаса прочности, соответствующий n пч» 4,0¸4,75; – при температуре нагрева стенки котла t = 250¸350 °С
где
Допускаемый коэффициент прочности продольного шва [ S ] выбрать из приложения 4 в зависимости от соотношения 0,5 qD и типа шва. Например, для однорядного нахлесточного шва при соотношении 0,5 qD = 0,44 МПа×м допускаемый коэффициент [ S ] = 0,6. Учитывая, что для тонкостенного сосуда smax = s1, определить зна-чение s1 по формуле (2.1) и вычислить толщину стенки котла по фор- Принять значение d с учетом добавки на коррозию металла D = 1¸3 мм. 2. После определения толщины стенки котла (d) по таблицам справочной литературы принять диаметр заклепки d и шаг заклепочного шва р (можно воспользоваться приложением 4). 3. Проверочный расчет проводится по напряжениям среза по фор-муле (2.3). При этом расчете герметичность шва (его плотность) обеспечивается выбором соответствующего допускаемого условного напряжения Сила Q 0 в формуле (2.3) определяется следующим образом:
где z – число заклепок на участке шва шириной, равной шагу р. Расчет на срез с силой Q 0 по формуле (2.7) является одновременно расчетом на плотность шва. 4. Если условие прочности выполняется, вычисляют остальные параметры шва: – расстояние от заклепки до края листа е = 1,65 d; (2.8) – расстояние между рядами заклепок е 1 = 0,5 р; (2.9) – толщина накладок (если они есть) d1 = 0,8d. (2.10) 5. После этого для заданного элемента стенки котла определяют нормальное и касательное напряжения на наклонной площадке. Например,
Рис. 2.3
Из теории напряженного состояния
где s1 и s2 – главные напряжения, определяемые по формуле (2.1); Ða – угол между наибольшим главным напряжением и внешней нормалью к наклонной площадке. Так как он отсчитывается по часовой стрелке, то имеет знак "–" (прямая задача плос-кого напряженного состояния). Ða = –60°.
Рис. 2.4 Если sa > 0, то напряжение растягивает площадку:
Если sa < 0, напряжение сжимает площадку:
Касательное напряжение (ta) изображается на рисунке в соответствии
6. После вычисления значений нормального и касательного напряжений на наклонной площадке надо нарисовать векторы sa и ta на рисунке. Пример 1. Вычислить статический момент треугольника относительно оси Х (рис. 3.1).
Решение:
А = y с =
Рис. 3.1 Пример 2. Вычислить статический момент прямоугольника относительно оси Y (рис. 3.1). Решение: Sу = Аx с, А = Статические моменты могут быть положительными, отрицательными и равными нулю. Оси, относительно которых статические моменты равны нулю, называются центральными осями. Если плоская фигура представляет собой совокупность фигур конечной формы, то координаты центра тяжести этой фигуры вычисляют по формулам
где S S Аi – сумма площадей отдельных плоских фигур конечной формы, из которых состоит сечение. Пример 3. Определить положение центра тяжести плоской фигуры, показанной на рис. 3.2. Размеры указаны в сантиметрах.
Рис. 3.2
– разделим фигуру 1 – прямоугольник 2 – треугольник с центром тяжести с 2 (рис. 3.3). Рис. 3.3 Площади фигур: А 1 = 10 × 50 = 500 см2, А 2 = – выберем произвольную систему координат Х 0 ОY 0 (рис. 3.3);
– вычислим статические моменты фигур 1 и 2 относительно осей ОХ 0 и ОY 0:
– вычислим координаты центра тяжести заданной фигуры по формулам (3.3) и (3.4):
– отметим точку центра тяжести С на рисунке. 3.2. Моменты инерции плоских сечений. К моментам инерции относят: осевые моменты Ix, Iу; полярный момент Ip; центробежный момент Iху. Формулы для определения моментов инерции отдельных плоских фигур приведены в приложении 6. При необходимости вычисления момента инерции плоской фигуры относительно оси, параллельной центральной, используют формулы теоремы Гюйгенса – Штейнера:
где Ix, Iу – осевые моменты инерции относительно искомых осей Х и Y,
А – площадь фигуры; х и у – расстояния между соответствующими параллельными осями. Пример 4. Вычислить момент инерции прямоугольника относительно оси Х 1.
Решение: момент инерции относительно центральной оси СХ, параллельной оси Х 1,
площадь А = bh; расстояние между осями Подставляем в формулу (3.5):
3.3. Моменты сопротивления плоских сечений. Моменты сопротивления определяются по формулам
где Wx, Wу – моменты сопротивления относительно осей Х и Y; Wp – полярный момент сопротивления; Ix, Iу, Ip – моменты инерции; х max, у max – расстояние от соответствующей оси до наиболее удаленной rmax – расстояние от полюса до наиболее удаленной от него точки. Формулы для определения Wx, Wу, Wp для отдельных плоских фигур приведены в приложении 6.
3.4. Радиусы инерции. Радиусы инерции определяются по формулам
где ix, iу – радиусы инерции; Ix, Iу – осевые моменты инерции; А – площадь рассматриваемой фигуры. Задание 3 Для указанного составного плоского сечения вычислить моменты инерции относительно осей, проходящих через центр тяжести этого сечения. Указания к выбору схемы задания Схема состоит из отдельных фигур (брус, двутавр, неравнобокий уголок, швеллер). Фигуры располагаются в двух положениях (табл. 3.1). В соответствии с номером студенческого билета изобразить брус Таблица 3.1
Порядок формирования схемы задания: 1. На расстоянии l 1 от верхнего (левого) края бруса разместить фигуру 1 На расстоянии l 2 от фигуры 1 разместить фигуру 2 так, чтобы фигу-
Фигуру 2 и ее положение выбрать по табл. 3.2. 2. От фигуры 2 отложить расстояние l 3 вниз (вправо), чтобы получить полную длину бруса. Таким образом, длина бруса составит сумму длин: l 1 + длина прилегающей к брусу части фигуры 1 + l 2 + 3. Фигуру 3 – двутавр разместить на той же стороне бруса, где находится фигура 1. Размещать двутавр следует таким образом, чтобы полка его располагалась на брусе. Края бруса и полки двутавра должны быть
Рис. 3.6 Толщину бруса (δ) и номера для двутавра, швеллера и неравнобокого уголка взять из табл. 3.2 в соответствии с номером студенческого билета.
Указания к выполнению задания 3 1. Заданное составное сечение необходимо вычертить на листе миллиметровой бумаги в масштабе 1:1. Формат бумаги (от А4 и более) выбирается в зависимости от размеров заданного сечения. 2. Из сортамента (см. приложения 7 – 9) выписать основные характеристики для двутавра, швеллера и неравнобокого уголка. Удобно выполнить это в виде таблицы (рис. 3.7). 3. По формулам (3.1) – (3.4) вычислить координаты центра тяжести сечения (см. пример 3). 4. На чертеже отметить полученную точку центра тяжести и провести через нее систему координат (Х, Y). 5. Используя формулы (3.5) и (3.6), вычислить моменты инерции На чертеже необходимо указать все расстояния, которые использовались в формулах расчета (см. рис. 3.1, 3.3, 3.4). Основная надпись на листе миллиметровой бумаги выполняется в соответствии с приложением 15.
Рис. 3.7
Кручение Задание 4. Для стального вала круглого поперечного сечения, загруженного в соответствии с данными, приведенными в табл. 4.1, необходимо: а) построить эпюру крутящих моментов; б) подобрать диаметр вала из условия прочности и условия жесткости, принять в) построить эпюру углов поворота поперечных сечений вала.
Для четных вариантов исходная схема вала изображена на рис. 4.1, для нечетных – на рис. 4.2.
Рис. 4.1
Рис. 4.2 Пример расчета Расчет выполнен для стального вала, показанного на рис. 4.3, находящегося под действием внешних моментов.
Рис. 4.3 Разделим вал на участки (в данном случае таких участков три). Применяя метод сечений, определяем крутящие моменты на каждом участке вала:
По полученным значениям строим эпюру На рис. 4.4 представлены сечения вала (рассматривать защемленный вал рекомендуется со свободного конца) и эпюра крутящих моментов.
Рис. 4.4
По формуле (4.2) определим наибольшие касательные напряжения
По формуле
Из условия жесткости
Так как левая часть неравенства (4.5) имеет размерность радиан на метр длины (рад/м), а относительный угол закручивания
Определяем диаметр вала:
Принимаем d = 0,11 м, следовательно, d 1 = 0,11 м; d 2 = 0,22 м; Для построения эпюры углов поворота сечений определим углы поворота на участках вала:
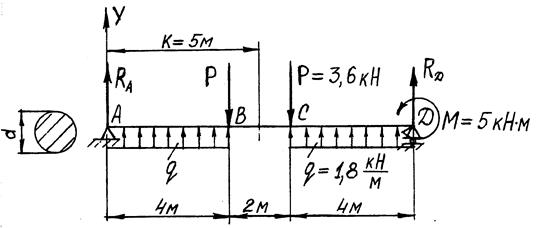
Учитывая, что защемленное сечение вала не поворачивается, эпюру углов поворотов начинаем строить с правого (защемленного) конца При z = 0 φ= 0. В сечении вала при z = 0,3 м откладываем значение В сечении вала при z = (0,3 + 0,4) м При z = (0,3 + 0,4 + 0,5) м Построенная эпюра углов закручивания вала приведена на рис. 4.4. Замечание. При построении эпюры углов закручивания вала значения j удобно представлять с коэффициентом 10– n. Так, в данной задаче этот коэффициент равен 10–3. Тогда эпюра j может быть подписана: j × 10–3, рад. Напряжения при изгибе Задание 5. Для стальной балки, загруженной в соответствии с данными, приведенными в табл. 5.1: а) построить эпюры поперечных сил и изгибающих моментов; б) подобрать размеры балки указанного профиля из условия проч-ности по нормальным напряжениям; в) проверить выбранное сечение по касательным напряжениям; г) построить эпюры нормальных и касательных напряжений для указанного сечения; Расчетную схему балки формируют на основании рис. 5.3 и данных табл. 5.1.
Рис. 5.3 Пример расчета Расчет выполнен для балки, показанной на рис. 5.4.
Рис. 5.4
|
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 484; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.70.0 (0.012 с.) |

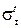 листовой стали, МПа. 65
листовой стали, МПа. 65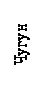


 ;
;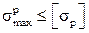 ;
; ,
, ,
,  ,
, 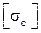 – допускаемые напряжения.
– допускаемые напряжения. ;
;  ;
;  м2.
м2. ;
;  ;
; 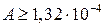 м2.
м2. ;
;  ;
;  м2.
м2. м;
м;
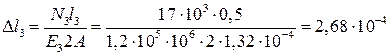 м;
м; м.
м.









 (2.4)
(2.4) , (2.5)
, (2.5) – предел прочности при растяжении материала листов, из которых выполнена стенка котла; значения
– предел прочности при растяжении материала листов, из которых выполнена стенка котла; значения  , (2.6)
, (2.6) – предел текучести материала листов котла при рабочей температуре котла. Рабочая температура котла задана в табл. 2.1;
– предел текучести материала листов котла при рабочей температуре котла. Рабочая температура котла задана в табл. 2.1; – коэффициент запаса прочности, соответствующий
– коэффициент запаса прочности, соответствующий  , (2.7)
, (2.7)
 , (2.11)
, (2.11)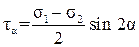 , (2.12)
, (2.12)





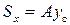 ;
; ;
; .
. , x с =
, x с = 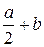 .
. , (3.3)
, (3.3) , (3.4)
, (3.4) , S
, S  – соответственно сумма статических моментов относительно осей Х и Y;
– соответственно сумма статических моментов относительно осей Х и Y;
 Решение:
Решение: см2;
см2; см3;
см3; см3;
см3; ;
;
 см;
см;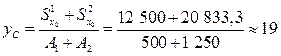 см;
см;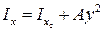 ; (3.5)
; (3.5) , (3.6)
, (3.6) – осевые моменты инерции относительно центральных осей данной фигуры;
– осевые моменты инерции относительно центральных осей данной фигуры;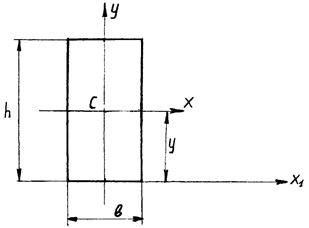 Рис. 3.4
Рис. 3.4
 (см. приложение 6);
(см. приложение 6); .
. .
. (3.7)
(3.7) (3.8)
(3.8)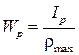 , (3.9)
, (3.9) ; (3.10)
; (3.10) , (3.11)
, (3.11)














 = 80 МПа;
= 80 МПа; 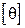 = 1 ˚/м;
= 1 ˚/м;


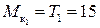 кН·м;
кН·м; кН·м;
кН·м; кН·м.
кН·м. .
.

 кПа;
кПа;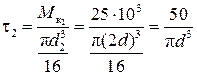 кПа;
кПа;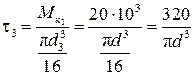 кПа.
кПа. , следовательно, расчет ведем по III участку.
, следовательно, расчет ведем по III участку. ;
;  ;
; 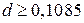 м.
м. определим значение относительного угла закручивания на каждом участке вала:
определим значение относительного угла закручивания на каждом участке вала: рад/м;
рад/м; рад/м;
рад/м; рад/м.
рад/м. .
. ˚/м
˚/м  рад/м.
рад/м. .
.
 рад;
рад; рад;
рад; рад.
рад. , равное
, равное  рад (знак "–", так как
рад (знак "–", так как  < 0).
< 0). рад.
рад. рад.
рад.