Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методичні вказівки і індивідуальні завданняСодержание книги
Поиск на нашем сайте
РОБОЧА ПРОГРАМА
Методичні вказівки і індивідуальні завдання До вивчення дисципліни «Вища математика» для студентів економічних спеціальностей
Затверджено На завісданні Вченої ради Академії Протокол № 1 від 27.01.04
Дніпропетровськ НМетАУ 2004 ББК 22.142 Робоча програма, методичні вказівки і індивідуальні завдання до вивчення дисципліни “Вища математика” для студентів економічних спеціальностей /Укл.: Г.Г. Швачич, О.Г. Холод, О.О. Шмукін – Дніпропетровськ: НМетАУ, 2004. – 52 с.
Наведені рекомендації до вивчення дисципліни “Вища математика”: робоча програма дисципліни, необхідний обсяг знань студентів в результаті її вивчення, основна і додаткова література, що рекомендується. Наведено варіанти індивідуальних завдань, що виконують студенти в процесі вивчення дисципліни. Призначені для студентів заочної форми навчання, які навчаються за економічними спеціальностями. Друкується за авторською редакцією.
Укладачі: Г.Г. Швачич, канд. техн. наук, доц., О.Г. Холод, канд. техн. наук, доц. О.О. Шмукін, канд. фіз.-матем. наук, доц.
Відповідальний за випуск: Г.Г. Швачич, канд. техн. наук, доц.
Рецензент Н.О. Різун, канд. техн. наук (ДУЕП)
ЗМІСТ
1. Робоча програма дисципліни “Вища математика”.................................. 4 2. Вказівки до виконання контрольних робіт.............................................. 9 3. Література.................................................................................................. 12 3.1. Основна……………………………………………………………………12 3.2. Додаткова………………………………………………………………….13 4. Задачі для виконання індивідуальних завдань........................................ 14 5. Таблиця варіантів індивідуальних завдань............................................. 43 5.1. Таблиця варіантів індивідуальних завдань №1,2………….………....43 5.2. Таблиця варіантів індивідуальних завдань №3,4........................... 44 5.3. Таблиця варіантів індивідуальних завдань № 5…………..…………..46 6. Орієнтовний перелік питань для підсумкового контролю знань.............47 1. РОБОЧА ПРОГРАМА ДИСЦИПЛІНИ "Вища математика " Розділ І. ЛІНІЙНА АЛГЕБРА МАТРИЦІ, ДІЇ З НИМИ
Поняття прямокутної матриці. Види матриць. Дії з матрицями та їх властивості.
ВИЗНАЧНИКИ. СИСТЕМИ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ
Визначники другого та третього порядків, методи їх обчислення. Визначники n–го порядку, їх властивості та обчислення. Системи лінійних алгебраїчних рівнянь (СЛАР). Основні поняття та означення. Правило Крамера для розв'язування СЛАР. Умови існування та одиничності розв’язку. Однорідні СЛАР, умови одиничності розв’язку. Матрична форма запису СЛАР. Поняття та знаходження оберненої матриці. Розв'язування СЛАР за допомогою оберненої матриці. Поняття рангу матриці. Методи знаходження рангу. Теореми про ранг матриці. Системи n лінійних алгебраїчних рівнянь з m невідомими. Умови сумісності й визначеності. Теорема Кронекера-Капеллі. Дослідження СЛАР. Розв'язування економічних задач. Розділ IІ. векторна АЛГЕБРА
Поняття скалярної та векторної величини. Рівність векторів. Лінійні операції над векторами: додавання, віднімання та множення на скаляр. Одиничний вектор. Колінеарність та компланарність векторів. Скалярний добуток векторів, його властивості та застосування. Векторна та скалярна проекція вектора на вісь. Властивості скалярної проекції вектора на вісь. Лінійна комбінація векторів. Лінійна залежність та лінійна незалежність векторів. Векторний базис на площині та у просторі. Розклад довільного вектора за базисом. Координати вектора у заданому базисі. Афінна система координат на площині та у просторі. Декартова прямокутна система координат (ДПСК). Декартові прямокутні координати вектора. Лінійні операції над векторами в координатах. Координати вектора, що сполучає дві точки. Скалярний добуток векторів у координатній формі запису. Використання скалярного добутку у векторній алгебрі. Умови перпендикулярності та коленіарності векторів. Приклади застосування векторної алгебри в економіці.
Розділ III. АНАЛІТИЧНА ГЕОМЕТРІЯ ПРЯМА ЛІНІЯ НА ПЛОЩИНІ
Метод координат. Лінії та їх рівняння. Пряма лінія на площині та її рівняння в декартових координатах. Загальне рівняння прямої та його дослідження. Канонічне та параметричне рівняння прямої. Рівняння прямої, яка проходить через дві точки. Рівняння у відрізках. Рівняння прямої з кутовим коефіцієнтом. Умови паралельності та перпендикулярності прямих. Кут між прямими. Рівняння пучка прямих. Нормальне рівняння прямої. Відстань від точки до прямої.
Поняття про криві другого порядку (Коло. Еліпс. Гіпербола. Парабола). Приклади застосування аналітичної геометрії на площині в економіці. ПЛОЩИНА ТА ПРЯМА У ПРОСТОРІ
Площина в просторі. Рівняння площини в просторі. Взаємне розташування двох площин в просторі (Кут між площинами. Умови паралельності та перпендикулярності). Пряма в просторі. Основні види рівняння прямої в просторі. Кут між прямими. Умови паралельності та перпендикулярності. Пряма та площина в просторі, їх взаємне розташування. Кут між прямою та площиною. Точка перетину. Гіперплощина. Приклади застосування аналітичної геометрії у просторі в економіці.
ОДНІЄЇ НЕЗАЛЕЖНОЇ ЗМІННОЇ Задачі, що приводять до поняття похідної. Означення похідної функції в точці, її геометричний, фізичний та економічний зміст. Рівняння дотичної та нормалі до плоскої кривої. Диференційованість функції у точці, на проміжку. Зв’язок між диференційованістю та неперервністю функції в точці. Правила диференціювання. Похідні основних елементарних функцій. Похідна складної функції. Похідна неявної, оберненої функцій. Таблиця похідних. Логарифмічне диференціювання. Похідні вищих порядків. Теорема Ферма, теорема Ролля, теорема Лагранжа, теорема Коші. Правило Лопіталя. Розкриття невизначеностей. Формула Тейлора. Умови зростання, спадання функції. Поняття екстремуму функції в точці. Необхідна та достатні умови екстремуму. Опуклість, угнутість, точки перегину графіка функції. Необхідна та достатні умови перегину. Асимптоти кривих. Повне дослідження функцій та побудова графіків за допомогою засобів математичного аналізу. Означення диференціала функції. Обчислення диференціала. Геометричний зміст диференціала. Властивості диференціала. Диференціал складної функції. Відшукання функції за її відомим диференціалом. Диференціали вищих порядків. Приклади застосування диференціального числення функції однієї незалежної змінної в економіці.
НЕЗАЛЕЖНИХ ЗМІННИХ Границя та неперервність функцій багатьох незалежних змінних. Повний та частковий приріст функції. Частинні похідні, повний диференціал функцій багатьох незалежних змінних. Похідні та диференціали вищих порядків. Похідна за даним напрямком. Градієнт функції. Безумовний та умовний екстремуми функцій багатьох незалежних змінних. Приклади застосування диференціального числення функції багатьох незалежних змінних в економіці. Розділ XI. РЯДИ Числові ряди. Основні поняття та означення. Необхідні та достатні умови збіжності. Теорема Лейбниця. Абсолютна та умовна збіжність. Ознаки збіжності рядів. Функціональні ряди. Степеневі ряди. Область збіжності. Диференціювання та інтегрування степеневих рядів. Розкладення функцій в степеневі ряди. Ряди Тейлора та Маклорена. Використання рядів для наближених обчислювань. Приклади застосування рядів в економіці. ІНДИВІДУАЛЬНИХ ЗАВДАНЬ Навчальним планом з дисципліни "Вища математика" передбачено виконання контрольних робіт. Кількість задач контрольної роботи визначається викладачем. Перед розв’язуванням задач необхідно вивчити відповідний розділ теоретичного матеріалу.
При виконанні контрольних робіт студент повинний строго дотримувати наступних правил. 1. Виконувати контрольні роботи строго за варіантом, номер якого вказує викладач. 2. Кожна контрольна робота виконується в окремому зошиті в клітку чорнилом будь-якого кольору, крім червоних. У зошиті повинні бути поля для рецензента; наприкінці зошита необхідно залишити кілька чистих аркушів для доповнень і виправлень відповідно до зауважень рецензента. 3. Оформлення обкладинки зошита повинно відповідати зразку: НМетАУ ІНДИВІДУАЛЬНЕ ЗАВДАННЯ №
з дисципліни "ВИЩА МАТЕМАТИКА"
студента економічного факультету
група _____ спеціальність__________
_______________________________________ (прізвище, ім'я та по батькові)
Варіант №
№ залікової книжки ________
Дата здачі роботи до деканату __________
Викладач _____________________
Дніпропетровськ
4. Перед рішенням кожної задачі вказується її умова, замінивши загальні дані конкретними зі свого варіанта. Розташовувати задачі необхідно в порядку зростання їхніх номерів, зберігаючи нумерацію. 5. Розв’язок задач обов’язково супроводжуються поясненнями, необхідними рисунками або графіками та посиланнями на відповідні теоретичні поняття та формули. 6. Після одержання прорецензованої роботи студент повинний уважно вивчити рецензію і виконати всі зауваження рецензента. 7. Робота, виконана з якими-небудь порушеннями перерахованих вище вимог, не зараховується і повертається студенту для переробки. 8. Студент, що не виконав хоча б одну контрольну роботу, до іспиту не допускається. 9. Якщо контрольна робота після перевірки не зарахована, треба виправити помилки згідно з зауваженнями рецензента. Це необхідно робити у кінці роботи (або в окремому зошиті), написавши спочатку титул “Робота над помилками”. Вносити зміни до тексту вже перевіреної роботи категорично забороняється. Доопрацьована контрольна робота надсилається для повторної перевірки разом з першим варіантом. 10. Номер варіанту контрольної роботи обирається згідно з двома останніми цифрами залікової книжки, або студентського квитка. При чому, якщо цей номер перевищує цифру 50, то номер контрольної роботи визначається наступним чином: від цифри 100 віднімається цифра, що відповідає двома останніми цифрами залікової книжки, або студентського квитка. Наприклад, якщо номер двох останніх цифр залікової книжки відповідає цифрі 48, то студент виконує 48 варіант. В разі, коли номер двох останніх цифр залікової книжки 85, то варіант контрольної роботи обирається наступним чином: 100-85=15 і студент виконує 15 варіант контрольної роботи.
ЛІТЕРАТУРА Основна 1. Вища математика. Навчально-методичний посібник для самостійного вивчення дисципліни. – К.: КНЕУ, 1999. 2. Барковський В.В., Барковська Н.В. Математика для економістів: Ч.1. – К.: Національна академія управління, 1997. 3. Солодовников А.С., Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике. Ч.1,2. – М.: Финансы и статистика, 1999. 4. Высшая математика для экономистов / под ред. Н.Ш. Кремера – М.: Банки и биржи, ЮНИТИ, 1997. 5. Сушко С.О., Фомичова Л.Я., Кагадий Т.С. Математика для економічних спеціальностей. – Дн-ск: НГА України, 1999. 6. Ляшенко И.Н., Ляшенко Е.И. Математика для экономистов. – Донецк.: ДонГУ, 1998. 7. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах ч.1,2. – М.: Высшая школа, 1980. 8. Запорожец Г.И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1966. 9. Каплан И.А. Практические занятия по высшей математике. – Харьков: Изд–во ХГУ, 1967. 10. Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1977. 11. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и студентов вузов. – М.: Наука, 1986. 12. ШвачичГ.Г. Лінійна алгебра в розрахунках середовища MATHCAD: Підручник: ДАУБП, 2000. – 236 с. 13. Швачич Г.Г. MATHCAD в інженерних та економічних розрахунках: Навчальний посібник. – Дніпропетровськ: НМетАУ-ІПК МК, 2000. – 72 с. 14. Швачич Г. Г. Сучасні інформаційні технології в математиці для економістів: Підручник.- К.: Центр навчальної літератури, 2003.- 368 с. Додаткова 1. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1969. 2. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов. – М.: Наука, 1969. 3. Вища математика. Основні означення, приклади і задачі. ч.1,2. – К.: Либідь, 1992. 4. Пискунов Н.С. Дифференциальное и интегральное исчисление, Т.1,2. – М.: Наука, 1982. 5. Минорский В.П. Сборник задач по высшей математике. – М.: Наука, 1969.
Задача 1
Задано вектори, зображені на малюнку. Побудувати їх лінійну комбінацію – вектор 1.1.

1.2.
1.4.
1.6.
1.9.
1.10.
Задача 2 Вектори
Виконати наступні операції: 1. Обчислити координати вектора 2. Знати довжину та напрям вектора 3. Знайти кут між векторами 4. Побудувати вектори
2.1.
2.2.
2.3.
2.4.
2.5.
2.6.
2.7.
2.8.
2.9.
2.10.
Задача 3 Розкласти заданий вектор 3.1.
3.2.
3.3.
3.4.
3.5.
3.6.
3.7.
3.8.
3.9.
3.10.
Задача 4 Задано координати вершин трикутника АВС. Знайти: 1. Рівняння сторони АВ. 2. Довжину сторони АВ. 3. Рівняння медіани, що проведена з вершини В. 4. Рівняння висоти, що опущена з вершини С. 5. Довжину висоти, що опущена з вершини С. 6. Рівняння прямої, що проходить через вершину С паралельно стороні АВ. 7. Внутрішній кут В у радіанах. До кожного пункту зробити малюнок (ескіз). А(-3, 2); В(1, 4); С(-3, 0) А(0, 1); В(5, 3); С(4, 0) А(2, 3); В(-4, 2); С(-1, 4) А(5, -1); В(-1, 4); С(3, - 3) А(3, 1); В(2, - 4); С(4, 0) А(5, 3); В(-2, 4); С(3, -1) А(0, 1); В(-3, 4); С(1, -5) А(1, - 2); В(4, -2); С(4, 0) А(-3, 1); В(3,2); С(0, -2) А(0, 1); В(4, - 1); С(-4, 2)
Задача 5
Знайти область визначення функції. Нанести її на числову вісь 5. 1. 5. 3. 5. 5. 5. 7. 5. 9. Задача 6
Побудувати графік функції y=f(x) шляхом перетворення графіків основних елементарних функцій.
Задача 7
Знайти наведені границі функцій не користуючись правилом Лопіталя
7. 1. a) d) 7. 2. a) d) 7. 3. a) d) 7. 4. a) d) 7. 5. a) d) 7. 6. a) d) 7. 7. a) d) 7. 8. a) d) 7. 9. a) d) 7. 10. a) d)
Задача 8
Знайти похідні наведених функцій 8. 1. a) c) e)
c) e)
c) e)
8. 4. a) c) e)
8. 5. a) c) e) 8. 6. a) c) e)
c) e)
8. 8. a) c) e)
8. 9. a) c)
8. 10. a) c)
Задача 9 Обчислити найбільше та найменше значення функції на заданому відрізку
Задача 10
Засобами диференціального числення дослідити функцию y=f(x) та побудувати її графік. 10.1. а) 10.2. а) 10.3. а) 10.4. а) 10.5. а) 10.6. а) 10.7. а) 10.8. а) 10.9. а) 10.10. а) Задача 11
Знайти область визначення функції
Задача 12
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 238; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.66.165 (0.014 с.) |

 .
.




















 задані своїми координатами.
задані своїми координатами. що є їх лінійною комбінацією.
що є їх лінійною комбінацією.

 та
та  .
.
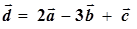




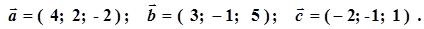













 за базисом
за базисом 




















 ; 5. 2
; 5. 2  ;
; ; 5. 4
; 5. 4  ;
; ; 5. 6
; 5. 6 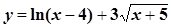 ;
; ; 5. 8
; 5. 8  ;
; ; 5.10
; 5.10  .
.









 ; b)
; b)  ; c)
; c)  ;
; ; e)
; e)  .
. ; b)
; b)  ; c)
; c)  ;
; ; e)
; e)  .
. ; b)
; b)  ; c)
; c)  ;
; ; e)
; e)  .
. ; b)
; b)  ; c)
; c)  ;
; ; e)
; e)  .
. ; b)
; b)  ; c)
; c)  ;
; ; e)
; e)  .
. ; b)
; b)  ; c)
; c) 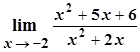 ;
; ; e)
; e)  .
. ; b)
; b) 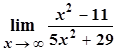 ; c)
; c)  ;
; ; e)
; e)  ; b)
; b)  ; c)
; c)  ;
; ; e)
; e)  .
. ; b)
; b)  ; c)
; c)  ;
; ; e)
; e)  .
. ; b)
; b)  ; c)
; c)  ;
; ; e)
; e)  .
. ; b)
; b)  ;
; ; d)
; d)  .
. ; f)
; f)  .
. 8. 2. a)
8. 2. a)  ; b)
; b)  ;
; ; d)
; d)  .
. ; f)
; f)  .
. 8. 3. a)
8. 3. a)  ; b)
; b)  ;
; ; d)
; d)  .
. ; f)
; f)  .
. ; b)
; b)  ;
; ; d)
; d)  .
. ; f)
; f)  .
. ; b)
; b) 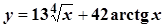 ;
; ; d)
; d)  .
. ; f)
; f)  .
. ; b)
; b)  ;
; ; d)
; d)  .
. ; f)
; f)  .
. ; b)
; b)  ;
; ; d)
; d)  .
. ; f)
; f)  .
. ; b)
; b)  ;
; ; d)
; d) 
 ; f)
; f)  .
. ; b)
; b)  ;
; ; d)
; d)  . e)
. e)  ; f)
; f)  .
. ; b)
; b)  ;
; ; d)
; d)  . e)
. e)  ; f)
; f)  .
.









 ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. . Побудувати таку область.
. Побудувати таку область.