
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачі для виконання індивідуальних завданьСодержание книги
Поиск на нашем сайте
Задача 1
Задано вектори, зображені на малюнку. Побудувати їх лінійну комбінацію – вектор 1.1.

1.2.
1.4.
1.6.
1.9.
1.10.
Задача 2 Вектори Виконати наступні операції: 1. Обчислити координати вектора 2. Знати довжину та напрям вектора 3. Знайти кут між векторами 4. Побудувати вектори
2.1.
2.2.
2.3.
2.4.
2.5.
2.6.
2.7.
2.8.
2.9.
2.10.
Задача 3 Розкласти заданий вектор 3.1.
3.2.
3.3.
3.4.
3.5.
3.6.
3.7.
3.8.
3.9.
3.10.
Задача 4 Задано координати вершин трикутника АВС. Знайти: 1. Рівняння сторони АВ. 2. Довжину сторони АВ. 3. Рівняння медіани, що проведена з вершини В. 4. Рівняння висоти, що опущена з вершини С. 5. Довжину висоти, що опущена з вершини С. 6. Рівняння прямої, що проходить через вершину С паралельно стороні АВ. 7. Внутрішній кут В у радіанах. До кожного пункту зробити малюнок (ескіз). А(-3, 2); В(1, 4); С(-3, 0) А(0, 1); В(5, 3); С(4, 0) А(2, 3); В(-4, 2); С(-1, 4) А(5, -1); В(-1, 4); С(3, - 3) А(3, 1); В(2, - 4); С(4, 0) А(5, 3); В(-2, 4); С(3, -1) А(0, 1); В(-3, 4); С(1, -5) А(1, - 2); В(4, -2); С(4, 0) А(-3, 1); В(3,2); С(0, -2) А(0, 1); В(4, - 1); С(-4, 2)
Задача 5
Знайти область визначення функції. Нанести її на числову вісь 5. 1. 5. 3. 5. 5. 5. 7. 5. 9.
Задача 6
Побудувати графік функції y=f(x) шляхом перетворення графіків основних елементарних функцій.
Задача 7
Знайти наведені границі функцій не користуючись правилом Лопіталя
7. 1. a) d) 7. 2. a) d) 7. 3. a) d) 7. 4. a) d) 7. 5. a) d) 7. 6. a) d) 7. 7. a) d) 7. 8. a) d) 7. 9. a) d) 7. 10. a) d)
Задача 8
Знайти похідні наведених функцій 8. 1. a) c) e)
c) e)
c) e)
8. 4. a) c) e)
8. 5. a) c) e) 8. 6. a) c) e)
c) e)
8. 8. a) c) e)
8. 9. a) c)
8. 10. a) c)
Задача 9 Обчислити найбільше та найменше значення функції на заданому відрізку
Задача 10
Засобами диференціального числення дослідити функцию y=f(x) та побудувати її графік. 10.1. а) 10.2. а) 10.3. а) 10.4. а) 10.5. а) 10.6. а) 10.7. а) 10.8. а) 10.9. а) 10.10. а) Задача 11
Знайти область визначення функції
Задача 12
Знайти частинні похідні 12.1. 12.2. 12.3. 12.4. 12.5. Задача 13 Задані функція
Задача 14
Знайти неозначені інтеграли 14.1. а) в) 14.2. а) в) 14.3. а) в) 14.4. а) в) 14.5. а) в) 14.6. а) в) 14.7. а) в) 14.8. а) в) 14.9. а) в) 14.10. а) в)
Задача 15
Обчислити означені інтеграли 15.1. а) 15.2. а) 15.3. а) 15.4. а) 15.5. а) 15.6. а) 15.7. а) 15.8. а) 15.9. а) 15.10. а) Задача 16 Розв”язати задачу, пов”зану з геометричними додатками означеного інтеграла
16.1. Обчислити площу фігури, обмеженої параболою y =х2 і прямою х-у-6=0. 16.2. Обчислити об”єм тіла, утвореного обертанням навколо осі ординат фігури, обмеженої параболами y =х2 і 16.3. Обчислити площу фігури, обмеженої лініями 16.4.Обчислити об”єм тіла, утвореного обертанням навколо осі ординат фігури, обмеженої лініями 16.5. Обчислити площу фігури, обмеженої параболою y =4-х2 і прямо y =х+2. 16.6.Обчислити об”єм тіла, утвореного обертанням навколо осі абсцис фігури, обмеженої лініями y =х3 і 16.7. Обчислити площу фігури, обмеженої параболою y =х2+4х і прямою x-у+4=0. 16.8.Обчислити об”єм тіла, утвореного обертанням навколо осі ординат фігури, обмеженої параболами y =3-х2 і y =х2+1. 16.9. Обчислити площу фігури, обмеженої параболою y =3-х2-2х і віссю абсцис. 16.10.Обчислити об”єм тіла, утвореного обертанням навколо осі абсцис фігури, обмеженої гіперболою ху=4, прямими х=3, х=12 і віссю абсцис.
Задача 17 Обчислити невласні інтеграли, або довести їх розбіжність 17.1. а) 17.2. а) 17.3. а) 17.4. а) 17.5. а) 17.6. а) 17.7. а) 17.8. а) 17.9. а) 17.10. а)
Задача 18
Знайти загальний розв”язок диференціального рівняння першого порядку 18.1.
18.3.
18.5.
18.7.
18.8.
18.9.
Задача 19
Знайти частнні розв’язки рівнянь, що задовольняють заданим початковим умовам
19.8.
19.9.
19.10. Задача 20 Перевірити, чи виконується необхідна умова збіжності ряда
20.1.
20.2.
20.3.
20.4.
20.5.
20.10.
Задача 21
Дослідити збіжність числового ряда
21.1. 21.2. 21.3. 21.4. 21.5.
Задача 22
Дослідити на абсолютну та умовну збіжність
22.1.
22.2.
22.3.
22.4.
22.5. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 .
.




















 задані своїми координатами.
задані своїми координатами. що є їх лінійною комбінацією.
що є їх лінійною комбінацією.

 та
та  .
.
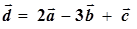




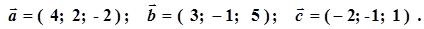













 за базисом
за базисом 




















 ; 5. 2
; 5. 2  ;
; ; 5. 4
; 5. 4  ;
; ; 5. 6
; 5. 6 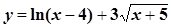 ;
; ; 5. 8
; 5. 8  ;
; ; 5.10
; 5.10  .
.









 ; b)
; b)  ; c)
; c)  ;
; ; e)
; e)  .
. ; b)
; b)  ; c)
; c)  ;
; ; e)
; e)  .
. ; b)
; b)  ; c)
; c)  ;
; ; e)
; e)  .
. ; b)
; b)  ; c)
; c)  ;
; ; e)
; e)  .
. ; b)
; b)  ; c)
; c)  ;
; ; e)
; e)  .
. ; b)
; b)  ; c)
; c) 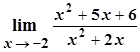 ;
; ; e)
; e)  .
. ; b)
; b) 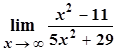 ; c)
; c)  ;
; ; e)
; e)  ; b)
; b)  ; c)
; c)  ;
; ; e)
; e)  .
. ; b)
; b)  ; c)
; c)  ;
; ; e)
; e)  .
. ; b)
; b)  ; c)
; c)  ;
; ; e)
; e)  .
. ; b)
; b)  ;
; ; d)
; d)  .
. ; f)
; f)  .
. 8. 2. a)
8. 2. a)  ; b)
; b)  ;
; ; d)
; d)  .
. ; f)
; f)  .
. 8. 3. a)
8. 3. a)  ; b)
; b)  ;
; ; d)
; d)  .
. ; f)
; f)  .
. ; b)
; b)  ;
; ; d)
; d)  .
. ; f)
; f)  .
. ; b)
; b) 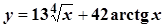 ;
; ; d)
; d)  .
. ; f)
; f)  .
. ; b)
; b)  ;
; ; d)
; d)  .
. ; f)
; f)  .
. ; b)
; b)  ;
; ; d)
; d)  .
. ; f)
; f)  .
. ; b)
; b)  ;
; ; d)
; d) 
 ; f)
; f)  .
. ; b)
; b)  ;
; ; d)
; d)  . e)
. e)  ; f)
; f)  .
. ; b)
; b)  ;
; ; d)
; d)  . e)
. e)  ; f)
; f)  .
.









 ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. . Побудувати таку область.
. Побудувати таку область.








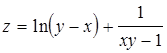
 и
и  функції
функції 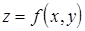 .
. 12.6.
12.6. 
 12.7.
12.7. 
 12.8.
12.8. 
 12.9.
12.9. 
 12.10.
12.10. 
 , точка А(хо,уо) та вектор а. Знайти: а) grad z в точці А; б) похідну в точці А за напрямком вектора а.
, точка А(хо,уо) та вектор а. Знайти: а) grad z в точці А; б) похідну в точці А за напрямком вектора а.









 ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г) 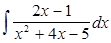 .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г) 
 ; б)
; б) 
 ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  ;
; ; г)
; г)  .
. ; б)
; б)  .
. ; б)
; б)  .
.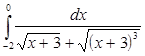 ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. .
. , ху=1 і прямою х=4.
, ху=1 і прямою х=4. і віссю абсцис.
і віссю абсцис. ; б)
; б)  .
.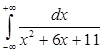 ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
.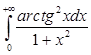 ; б)
; б)  .
. 18.2.
18.2. 
 18.4.
18.4. 
 18.6.
18.6. 


 18.10.
18.10. 



















 20.6.
20.6. 
 20.7.
20.7. 
 20.8.
20.8. 
 20.9.
20.9. 


 21.6.
21.6. 
 21.7.
21.7. 
 21.8.
21.8. 
 21.9.
21.9. 
 21.10.
21.10. 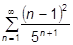
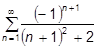 22.6.
22.6. 
 22.7.
22.7. 
 22.8.
22.8. 
 22.9.
22.9. 



