
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 3. Обработка результатов измерений.Содержание книги
Поиск на нашем сайте 3.1. Выбор количества измерений.
Цель любого измерения – это получение результата измерений с оценкой действительного значения измеряемой величины. Для достижения конечной цели проводится обработка результатов измерений. При этом выбор методов обработки результатов измерений определяется следующими факторами: - форма закона распределения результатов измерений; - применяемый метод измерений (прямой, косвенный); - количество выполненных измерений искомой величины. В метрологической практике используются следующие законы распределения:
1. Равномерный закон. Используется в случаях когда результаты измерений сосредоточены на интервале от “a” до “b” при постоянной величине плотности на этом интервале и при равенстве его нулю вне указанного интервала. Плотность распределения записывается в виде:
F(x) = F(x) График имеет вид:
a b
Равномерный закон распределения обычно применяют при выполнении равномерного квантования непрерывных величин по уровню в цифровых измерительных приборах. Для этого случая количество измерений около 6. 1.Для средств измерений, у которых погрешности изменяются в зоне нижней и верхней границ поля допуска используют закон, у которого плотность распределения имеет вид:
Количество измерений около 10.
2.К наиболее часто используемых законам относится нормальный закон распределения, плотность которого имеет следующий вид:
Где
Например, Следующим (третьим) параметром, определяющим число измерений, является доверительная вероятность, т.е. вероятность того, что
Если распределение погрешности подчиняется нормальному закону это уже определяет и доверительную вероятность. Например, при P = 0.95 Таблица
Из таблицы видно, что на практике число достоверных измерений обычно берутся в пределах до 20…30 измерений. Если же закон распределения заранее неизвестный, то число измерений должно увеличиваться во много раз для нахождения этого закона. При этом по результатам измерений рассчитывают среднее квадратическое значение, которое является оценкой математического ожидания величины, а также статическое среднеквадратическое отклонение (СКО).
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 171; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.70.101 (0.008 с.) |


 , F(x)
, F(x)

 - математическое ожидание величины
- математическое ожидание величины  ,
, - среднее квадратическое отклонение необходимое число измерений при нормальном законе распределения случайной величины зависит от погрешности измерения, и коэффициента вариации, определяемой выражением:
- среднее квадратическое отклонение необходимое число измерений при нормальном законе распределения случайной величины зависит от погрешности измерения, и коэффициента вариации, определяемой выражением: , или
, или 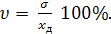
 = 0,33…0,35 можно считать, что распределение случайной величины подчиняется нормальному распределению.
= 0,33…0,35 можно считать, что распределение случайной величины подчиняется нормальному распределению. результата измерения находится в интервале:
результата измерения находится в интервале:
 - заранее заданная произвольно малая величина.
- заранее заданная произвольно малая величина. Таким образом, для определения числа измерений необходимо знать три параметра – погрешность измерения, коэффициент вариации и доверительную вероятность.
Таким образом, для определения числа измерений необходимо знать три параметра – погрешность измерения, коэффициент вариации и доверительную вероятность.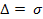 значение P = 0.68, при
значение P = 0.68, при  значение P = 0.95, а при
значение P = 0.95, а при  значение P = 0.99, где
значение P = 0.99, где  - СКО.
- СКО.


