
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эталон единицы силы электрического токаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Серьезные задачи стоят перед метрологами в области совершенствования эталонов электрических единиц. Измерения электрических величин начались с изучения статического электричества и построения электростатических генераторов. Электростатический принцип (притяжение между разноименно заряженными электродами) лежит в основе ряда приборов, измеряющих большие значения постоянных напряжений. Например, электростатический генератор Ван-де-Граафа служил для придания электронам или протонам энергий в несколько миллионов электрон-вольт. Электромагнитные явления наука открыла лишь к концу XVIII в. (закон Кулона — 1785 г.; гальваническая батарея Вольта («вольтов столб») — 1799 г.; закон Ампера — 1820 г.; закон Ома — 1826 г.; закон электромагнитной индукции Фарадея — 1831 г.). Первые единицы электрических величин появились в 30—40-х годах XIX столетия. Многие ученые пользовались своими собственными единицами. Например, в 1848 г. Б.С. Якоби изготовил в качестве эталона единицы сопротивления медную проволоку длиной 25 футов и весом 345 гран (около 0,635 Ом). Для измерения напряжения применяли даниель и бунзен — единицы, равные электродвижущей силе (ЭДС) соответствующих гальванических элементов. В 1860 г. немецкий электротехник и предприниматель Вернер Сименс впервые в мире создал высокостабильный ртутный эталон единицы электрического сопротивления — стеклянную трубку определенной длины и сечения, заполненную ртутью. Появилась еще одна единица — сименс. В 1861 г. Британская ассоциация развития науки назначила специальную комиссию по электрическим единицам, в состав которой вошли видные ученые мира — У. Томсон (лорд Кельвин), Д. Максвелл, В. Сименс и др. В основу своей деятельности комиссия положила абсолютную систему (СГСМ), но поскольку ее единицы оказались слишком велики или слишком малы для практики, она (комиссия) установила практические единицы, образованные путем умножения единиц СГСМ на 10 в соответствующей положительной или отрицательной степени. В 1863 г. комиссия приняла практические единицы — ом (109 единиц СГСМ) и вольт (108 единиц СГСМ), а в 1867 г. - фарад (Ю-9 единиц СГСМ). С этого времени электрики всего мира обрели общий язык. Официальное принятие этих практических единиц многими странами, в том числе и Россией, связано с I Международным конгрессом электриков 1881 г. На конгрессе было принято решение об организации Комиссии единиц, в которую вошли А.Г. Столетов (от России), Г. Гельмгольц, В. Том- сон, Дж.У. Рэлей, Г.Р. Кирхгоф, К. Клазиус, Р. Беккерель и др. По предложению А. Г. Столетова было принято постановление о электрических единицах (названных абсолютными практическими), где для электрических измерений принимаются основные единицы СГС — сантиметр, грамм-масса, секунда.
В 1884 г. Международная конференция электриков (МКЭ) приняла новое решение, установив, что ампер равен 0,1 единицы СГСМ, и приняв его в качестве основной единицы наряду с омом. При изготовлении эталонов для абсолютных практических электрических единиц возникли многочисленные трудности, поэтому в 1893 г. МКЭ ввела новые практические электрические единицы, которые получили название международных и просуществовали до 1948 г. В 1908 г. на лондонской Международной конференции по электрическим единицам и эталонам за ампер был принят ток, при прохождении которого через раствор азотнокислого серебра выделяется 0,00118 г серебра за 1 с. Омом принято считать сопротивление столба ртути высотой 106,3 см и массой 14,4521 г. Это были первые определения ампера и ома, которые, по существу, давали и способы их воспроизведения. Особенность этих единиц состояла в том, что они не вытекали из законов электричества и магнетизма и не были связаны с механическими единицами, поэтому ватт механический и ватт электрический различались на 0,02%. Повышение точности измерений требовало ликвидации этого расхождения. Проблема была решена при введении Международной системы единиц. В этой системе ампер воспроизводится в устройстве, называемом токовыми весами, а ом — набором эталонных катушек сопротивления. На IX Генеральной конференции по мерам и веса было принято следующее определение ампера: «Ампер — сила неизменяющегося тока, который, проходя по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого круглого сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызвал бы между этими проводниками силу, равную 2 • Ю-7 Н на каждый метр длины» (рис. 7.10).
В основу определения ампера положен закон Ампера (1820) о взаимодействии токов. Для воспроизведения этой единицы наибольшее распространение получило устройство, называемое токовыми весами. Весами это устройство названо в силу того, что взаимодействие двух проводников (в виде соленоидов) уравновешивается гирями. Установка состоит из весьма точных и чувствительных равноплечих весов (рис. 7.11). К серьгам коромысла весов подвешены два одинаковых соленоида. Один из них — рабочий, другой служит для создания симметричной нагрузки на коромысло. Рабочий соленоид помещается внутри неподвижного соленоида. Через эти два со-
Рис. 7.11. Схема устройства токовых весов леноида пропускается один и тот же ток. В результате взаимодействия соленоидов на подвижный соленоид действует сила, пропорциональная квадрату силы тока. Эта сила уравновешивается силой тяжести гирь. Сила тока определяется по формуле /2 = mg/F, где т — масса гирь, уравновешивающих силу взаимодействия; g — ускорение свободного падения; F— постоянная токовых весов, зависящая от геометрических размеров соленоидов, числа витков, шага намотки и других параметров, поддающихся расчету. Относительная погрешность данного метода не превышает б • Ю-6. Единицу тока можно определить и с помощью момента силы, действующей на катушку с током. Данная установка имеет прототип — так называемые весы Гельмгольца. Как видно из рис. 7.12, используется фиксированная катушка 7 длиной около 100 см, диаметром 28 см, в которой монтируются передвижные весы с измерительной катушкой 2. Ось измерительной катушки направлена перпендикулярно к оси фиксированной катушки. Диаметр измерительной катушки составляет 11,6 см при длине 25 см. В принципе ток, проходящий через фиксированную катушку 1, создает направленное по горизонтали магнитное поле Н0, в то время как у измерительной катушки имеется магнитный момент. Это вызывает появление момента силы D = М- Н0, который и подлежит измерению. Момент силы можно также рассчитать исходя из взаимной индукции. Для этого добиваются того, чтобы токи, текущие через катушки 7 и 2, были равны и постоянны во времени, а при изменении
направления одного из них на обратное одновременно перемещают разновесы. В этом случае момент силы выражается как D = [i0N]N2I2f(dvd2,L), где L — длина катушки 7; dx — ее диаметр; d2 — диаметр измерительной катушки (ее длина в выражение для момента силы не входит); N\ = 1000, N2 = 140 — число витков; р0 — магнитная проницаемость вакуума. Относительная погрешность метода не превосходит 8-Ю-6, что, конечно, несравнимо с точностью измерения времени и длины. Более того, ампер-весы — это уже технический анахронизм, а значение ампера определяется так, как это предложил А. Г. Столетов еще в 1881 г. Поэтому есть определенные надежды, что эталон ампера будет усовершенствован. Эталон единицы температуры Понятие «температура» возникло из ощущения теплого и холодного состояния тела. В основе ощущения этого состояния лежал тот факт, что два соприкасающихся тела по прошествии некоторого времени становятся одинаково теплыми, т. е. принимают одинаковую температуру.
Слово «температура» в переводе с латинского означает «смесь». Начало научного определения температуры связано с первым толкованием понятия «теплота». Физическая природа теплоты определялась на основе двух гипотез. Первая из них была сформулирована в 1613 г. Галилеем. Согласно этой гипотезе теплота является веществом, для которого применим закон сохранения. Количество такого вещества в физическом объекте определяет его температуру. Термометр показывает «крепость» смеси теплорода (флогистона) с материей. Вторая гипотеза высказана в 1620 г. Бэконом. Согласно его теории, теплота — это характеристика энергии мельчайших частей материи. Механическая теория теплоты получила подтверждение и развитие в работах М.В. Ломоносова. Следует отметить, что прошел довольно длительный период прежде чем на смену субъективным впечатлениям при определении температуры не пришли точные и единые методы измерений. Развитие методов измерения температуры стало возможным лишь тогда, когда были установлены такие свойства тел, которые зависят от температуры (длина, объем и т. д.) и которые можно было измерить объективно.
Попытки наглядного представления температурных изменений (охлаждения и нагревания) известны еще с древности. Филон Византийский (300 г.) и Герон Александрийский (130 г.) использовали для этой цели термическое расширение воздуха. На рис. 7.13,(7 изображен эскиз термоскопа Герона. Шаровой сосуд, заполненный водой и воздухом, выставляется под лучи солнца. Воздух расширяется и вытесняет воду из сосуда, которая попадает в резервуар и после охлаждения вновь поднимается по вертикальной трубке в сосуд. Таким образом, вытеснение воды означает нагревание. В 1592 г. Галилей вновь использовал этот принцип: в его термоскопе (рис. 7.13,6) по высоте водяного столба можно судить о том, является температура высокой или низкой. О применении такого прибора для измерения температуры воды упомянуто в 1611 г. Несмотря на простоту прибор был очень чувствительным, хотя и реагировал кроме темпе В 1636 г. впервые появилось слово «термометр». Так назывался прибор голландца К. Дреббеля — «дреббелев инструмент» — для измерения температуры, имевший восемь делений. На основании теплового расширения жидкостей в 1657 г. во Флоренции был создан термометр, наполненный спиртом. При этом было замечено, что можно пренебречь малыми температурными изменениями материала термометра, так как газы обладают наибольшим тепловым коэффициентом расширения.
Ранее при использовании эмпирических методов понятие «температура» оставалось неясным. Лишь с развитием учения о теплоте в начале ХУГИ в. потребовалось определение этого понятия. В 1662 г. Р. Бойль и в 1676 г. Э. Мариотт независимо друг от друга установили взаимосвязь между давлением и объемом газа при постоянной температуре (закон Бойля—Мариотта: pV= const при Т= const). Затем французский физик Г. Амонтон обнаружил, что в Париже при наибольшей летней жаре и наибольшем зимнем холоде величины давления газа соотносятся как 6:5. Он предложил определить температуру на основании давления газа внутри заданного объема. Тем самым он пришел к идее абсолютного нуля, т.е. температуры, при которой давление оказывается нулевым (1702). И. Ньютон в работе «О шкале степеней тепла и холода» (1701) описал 12-градусную шкалу, в которой 0° соответствовал температуре замерзания воды, а 12° — температуре тела здорового человека. Все эти и многие другие термометры были газовыми — при нагревании в них расширялся воздух. Однако идея определения температуры путем измерения давления газа не получила в то время распространения. Вместо газовых стали использоваться жидкостные термометры и подходящие для них температурные шкалы. Было установлено, что определенные процессы в одних и тех же условиях всегда протекают при одинаковых температурах, например таяние льда или кипение воды при постоянном давлении. Такие состояния вещества, в которых разные фазы при постоянной температуре находятся в равновесии, принимаются в качестве опорных точек. Их удобно использовать как калибровочные точки для температурной шкалы. Температурная шкала жидкостного термометра задается следующим образом: отмечается высота столба жидкости в двух опорных точках и полученный промежуток делится определенным образом. Разность между двумя соседними отметками обозначается «град» (или Первый жидкостный термометр, похожий на современный градусник, был сделан немецким физиком Г. Фаренгейтом. Конструируя спиртовые и ртутные термометры более 15 лет, он понял, как добиться их идентичности и большей точности показаний: нужно взять несколько точек с известной температурой, нанести их значения на шкалы и разделить расстояния между ними. В 1714 г. Фаренгейт ввел для сконструированного им спиртового термометра шкалу, в которой он, следуя идее Реомюра, в качестве опорных точек выбрал температуру таяния льда и температуру человеческой крови. Этот температурный интервал был разделен на 64 части, а нулевая точка помещалась ниже точки таяния льда на расстоянии, равном половине этого интервала; в то время это была наиболее низкая из известных (суровая зима 1709 г.) температур, она получалась путем смешивания нашатыря и смеси вода + лед. Таким образом, температура таяния льда имела значение 32 °F, а температура человеческой крови — значение 96 "F. В дальнейшем Фаренгейт перешел к ртутному термометру и выбрал в качестве верхней опорной точки точку кипения воды, для которой, сохраняя первоначальную шкалу, было установлено значение 212 °F.
В начале XVIII в. в России были распространены, но продержались недолго термометры петербургского академика Ж. Делиля со 150°-ной шкалой. Их вытеснила температурная шкала, пришедшая из Франции. Во Франции и России употреблялась шкала Реомюра, созданная в 1730 г. Французский натуралист, ученый с широким кругозором, Р.Реомюр построил ее в соответствии с тепловым расширением жидкости. Обнаружив, что при нагревании смесь воды со спиртом между температурами замерзания и кипения воды расширяется на 80 тысячных своего объема (современное значение - 0,008), Реомюр разделил этот интервал на 80 градусов. То есть в качестве опорных точек им были выбраны точки таяния льда и кипения воды. Точка таяния льда получила значение 0 °R. Свой термометр Реомюр наполнил смесью спирт + вода, которая между двумя опорными точками расширяется на 8%. За 1 °R была принята температура, соответствующая расширению жидкости на 1 %о (%о — промилле — тысячная доля). Поэтому температура кипения воды получила значение 80 °R. Термометры Реомюра использовались без малого два века и только к середине XX в. окончательно уступили место термометрам Цельсия с современной 100°-ной шкалой. Хотя справедливости ради надо сказать, что 100°-ная шкала была предложена за полвека до него. Около 1738 г. К. Линней, создатель научной системы классификации живых организмов, решил отметить температуру замерзания воды 0°, а температуру кипения воды — 100°. Термометр с такой шкалой был изображен на титульном листе книги Линнея, изданной в 1738 г. Цельсий предложил свою шкалу в 1742 г., т. е. четырьмя годами позже, причем его шкала была «обратной»: точка кипения воды была принята за 0°, а точка замерзания — за 100°. Используемая сегодня шкала Цельсия «перевернута» и введена позднее Штремером. Принцип работы жидкостных термометров сохранился по сей день: в качестве рабочего вещества используется ртуть или этиловый спирт, а при низких температурах — пентан. Их коэффициент объемного расширения значительно больше, чем у материала, из которого сделан термометр (стекло) (табл. 7.4).
Незначительное расширение жидкостей между 0 и 100 °С становится заметным, если наблюдать движение столбика жидкости в капилляре, из которого откачали воздух и соединили с (большим) резервуаром, содержащим рабочую жидкость. Поэтому условием высокой точности термометра является неизменный диаметр капилляра. Источником погрешностей служат термические свойства стекла. К существенным недостаткам жидкостных термометров относится зависимость показаний от рабочего вещества. У термометров с различными жидкостями, прокалиброванных в опорных точках, высота поднятия столбиков жидкостей в капиллярах при одинаковых температурах различна вследствие разных зависимостей коэффициентов расширения от температуры (нелинейность термического расширения). Так, в спиртовом термометре по сравнению с ртутным интервал между 0 и 100 °С необходимо делить неравномерно. По этой причине жидкостные термометры не годятся для определения понятия температуры, так как бессмысленно базисную величину делать зависимой от свойств определенного вещества. Количественные методы измерения температуры начали развиваться в XVII столетии; первые попытки унифицировать эти измерения относятся к 1887 г., т. е. начались приблизительно через столетие после введения метра в качестве единого эталона длины. Наряду с этим развивалось само понятие температуры: от субъективных впечатлений (тепло и холодно) до современного понимания термодинамической температуры, которая как интегрирующий множитель, ведущий к энтропии, играет основополагающую роль. Для нужд термодинамики необходимо было ввести понятие еще одной базисной величины — температуры. Развитие термодинамики в середине XIX столетия позволило дать новое, не зависящее от вещества определение температуры. Карно в 1824 г. теоретически разработал идеальную тепловую машину, которая позволяла преобразовывать тепло, получаемое в процессе обратимых (циклических) изменений состояния рабочего вещества, в механическую работу. Изменение состояния называется циклическим (обратимым), если тепловой процесс может быть пройден в обратном направлении через ту же последовательность состояний системы, причем система по возвращении из конечного состояния в начальное и окружающая среда остаются без изменений. К концу XVIII в. число различных температурных шкал приблизилось к двум десяткам, что было и неудобно, и не нужно. Кроме того, вскоре выяснилось, что даже тщательно проградуированные приборы с разными жидкостями показывают разную температуру. При 50 °С по ртутному термометру спиртовой показывал 43 °С, термометр с оливковым маслом — 49 °С, с чистой водой — 25,6 °С, а с соленой — 45,4 °С. Выход нашел известный английский физик У. Томсон. В 1848 г. он предложил измерять не температуру, а количество тепла, которое в определенном процессе, называемом циклом Карно, передается от горячего тела к холодному: оно определяется только их температурами и совершенно не зависит от нагреваемого вещества. В термодинамической, или абсолютной, шкале температур, основанной на этом принципе, единица температуры называется кельвин в честь автора — физика У. Томсона (лорда Кельвина). Термодинамическая температурная шкала была предложена Кельвином на основании следствия, вытекающего из второго закона термодинамики. Согласно этому следствию отношение количества теплоты Q,, получаемой от нагревателя любым телом, к количеству теплоты Q2, отдаваемому им холодильнику при обратимом цикле, равно отношению температур Тх и Т2 нагревателя и холодильника: q2 Т2 Кельвин (Томсон), исходя из пропорциональности газотермометрической и термодинамической температур, которая существует всегда, предложил, чтобы разность термодинамических температур между точками замерзания и кипения воды составляла 100 °С. Однако определение температуры с помощью этих двух опорных точек имеет недостаток - точность абсолютной газотермометрической и соответственно термодинамической температур зависит от экспериментально найденного коэффициента расширения. Хотя на основании предыдущего соотношения следовало бы, как это уже предлагалось Амонтоном, определять значение температуры одной опорной точки (вторая — точка абсолютного нуля). Такое определение температуры было введено лишь почти через 100 лет. На X Генеральной конференции по мерам и весам в 1954 г. было принято, что термодинамическая температура тройной точки воды содержит точно 273,16 Кельвина (К). Тройная точка воды — это такая точка на диаграмме состояния, в которой жидкое, твердое и газообразное агрегатные состояния вещества одновременно находятся в равновесии друг с другом. На рис. 7.14 представлена диаграмма трех агрегатных состояний (или фаз) воды. Согласно правилу фаз Гиббса /= с — р + 2, где /— число степеней свободы системы (число независимо выбираемых переменных); р — число фаз; с — число компонент. Для чистой воды (с — 1) число степеней свободы /= 3 — р. При наличии одной фазы можно свободно выбрать две переменные, например давление и температуру. Если в равновесии находятся две фазы (р = 2), то / = 1, т. е. для произвольно выбранной температуры существует лишь одно определенное значение давления, при котором система находится в равновесии.
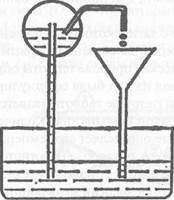
Этот случай иллюстрируется кривыми на диаграмме состояния, которые делят всю область на твердую, жидкую и газообразную фазы (кривые давления пара, сублимации, таяния). В точке пересечения трех кривых сосуществуют все три фазы (р= 3), так что система не имеет больше степеней свободы {f = 0). При изменении переменной нарушается равновесие системы. Три фазы могут одновременно существовать только при совершенно определенных значениях давления и температур. Для воды р = 611 Па и Т = 273,16 К (по определению). В то же время при одновременном существовании трех агрегатных состояний мы всегда имеем одну и ту же температуру. В противоположность этому при задании, например, температуры кипения или плавления нам всегда необходимо задавать соответствующее давление. Воспроизводимые состояния равновесия между фазами чистых веществ принимаются в качестве опорных точек. Тройная точка воды выбрана из тех соображений, что ее можно легко получить и воспроизвести в температурном интервале меньше миллиградуса. Точка замерзания воды при нормальном давлении (р= 101 325 Па = = 1 атм) расположена ниже тройной точки воды примерно на 0,00993°. В пределах экспериментальной точности она не отклоняется от использовавшегося ранее значения температуры точки замерзания; по этой причине нулевая точка шкалы Цельсия составляет Г0 = 273,15 К. Определяемая с такой же точностью точка кипения воды при нормальном давлении составляет 373,15 К, хотя при более точных измерениях она может несколько отклониться от этого значения. Таким образом, если одной температуре придать какое-либо значение, например температуре Т2 — значение тройной точки воды, и если будет известно отношение количества теплоты Qj /Q2, to можно определить температуру Тх. На рис. 7.15 приведена схема сосуда, применяемого для определения тройной точки воды. Термодинамическая температура может быть выражена и в градусах Цельсия (°С) с помощью соотношения t= Т— 273,15 К, где t — температура Цельсия; Т- температура Кельвина; 273,15 К - температура точки таяния льда по шкале Кельвина. Установление
температуры 70 позволяет дать новое термодинамическое определение температуры Цельсия. Ввиду того, что t=T—TQ, температура Цельсия является производной величиной. Графические соотношения различных температурных шкал приведены на рис. 7.16. В 1967 г. на XIII Генеральной конференции по мерам и весам впервые было дано определение температурной шкалы и принята в качестве единицы температуры 1/273,16 часть тройной точки воды. Воспроизведение термодинамической шкалы представляет большие трудности, поэтому VII Генеральная конференция по мерам и весам (1927) приняла, а IX Генеральная конференция (1948) утвердила международную практическую температурную шкалу, воспроизводимую по определенным постоянным реперным точкам. Она представляла собой шкалу Цельсия, единица которой (1 °С) определялась с помощью интервала между точкой таяния льда (t = О °С) и точкой кипения воды (t= 100 °С). В области температур
от —183° до 1063 °С эта шкала была реализована посредством четырех других опорных точек: точек кипения кислорода (—183 °С) и серы (445 °С), точек плавления серебра (962 °С) и золота (1063 °С). Для измерения температур использовались три прибора: в области температур от — 183 до 660 °С — термометр сопротивления, от 660 до 1063 °С — термоэлемент, выше 1063 °С — пирометр. Термодинамическая шкала была хороша всем, кроме одного: в повседневной практике тепловые измерения с последующими расчетами крайне неудобны, да и сам цикл Карно, прекрасно изученный теоретически, трудно воспроизвести не в специализированной метрологической лаборатории. С XVIII в. развитие термометрии шло по линии разработки, наряду с термодинамической, практических температурных шкал. Именно практические шкалы и воспроизводятся современными национальными эталонами.
В связи с тем, что на X ГКМВ (1954) в качестве базисной величины Международной системы единиц была установлена температура точки воды 273,16 К, в 1960 г. на XI ГКМВ Международную температурную шкалу-1948 переименовали в Международную прак В табл. 7.5 приведены опорные точки МПТШ-68, а также оценочные погрешности, с которыми эти точки устанавливались. Температуры опорных точек даны для нормального давления р =
= 101 325 Па (1 атм), за исключением тройных точек и точки кипения водорода. Альтернативой точке кипения воды является точка затвердевания олова (ґ68 = 231,9681 °С с оценочной погрешностью 0,915 К). Интерполяция между температурами постоянных точек производится по формулам, устанавливающим связи между показаниями специфицированных аттестованных интерполяционных приборов и значениями международной практической температуры. В качестве постоянных точек используются равновесия между двумя фазами чистых веществ: жидкой и газообразной (точки кипения) или твердой и жидкой (точки затвердевания). В трех случаях используются так называемые тройные точки, характеризуемые равновесием между твердой, жидкой и парообразной фазами водорода, кислорода и воды. Точность воспроизведения Кельвина и градуса Цельсия различна в разных интервалах температур. Наибольшая точность воспроизведения достигается в тройной точке воды. Международные температурные шкалы неоднократно изменялись за последние 100 лет в соответствии с растущими требованиями к точности и диапазонам измерений: • 1889 г.: МКМВ-1887 - эталонная водородная температурная шкала 1887 г., температурный диапазон от —50 до 100 °С; 1927 г.: МТШ-27 — международная температурная шкала 1927 г., температуры выше — 190°С; 1948 г.: МПТШ-48 — международная температурная шкала 1948 г., температуры выше — 182,97°С; 1960 г.: МТПШ-48 — международная практическая температурная шкала 1948 г. (улучшенное издание 1960 г.), температурный диапазон как у МТПШ-48; 1968 г.: МПТШ-68 — международная практическая температурная шкала 1968 г., температуры выше 13,81 К; 1975 г.: МПТШ-68 (75) — международная практическая температурная шкала 1968 г. (улучшенное издание 1975 г.), температурный диапазон как у МПТШ-68; 1978 г.: ПТШ-76 — временная температурная шкала 1976 г. в температурном диапазоне 0,5-30 К; 1984 г.: температурная шкала в диапазоне 14—273,16 К (замкнутые ячейки тройной точки) (МПТШ-68); с 1989 г. по настоящее время: температурная шкала в диапазоне 0,5—10 К (устройства для реперных точек на сверхпроводниках) (МТШ-90). Здесь буква «П» («практическая») опущена, поскольку разница между практической и теоретической (термодинамической) температурами ничтожно мала. Тем самым область определения МТШ-90 увеличена на разность Тмтш 90 — 7МТШ68. Единица термодинамической температуры в МТШ-90 не изменилась (кельвин, или К). Без изменений также осталась связь температуры Кельвина с температурой Цельсия t, осуществляемая известным соотношением t= Т— 273,15 К. Существующие значительные расхождения между значениями 7,мтш 90 и 7M|1T|IJ 68 учитываются при анализе результатов измерений температуры с помощью средств измерений, проградуированных по разным шкалам. Можно выделить четыре основные группы различий шкал МТШ-90 и МПТШ-68, касающихся: > области определения шкал; > средств воспроизведения единицы температуры; > специальных требований; > интерполяционных зависимостей. Государственные первичные эталоны России воспроизводят МТШ-90 в двух поддиапазонах: 0,8-273,16 К и 273,16-2773 К. В состав первого эталона в качестве основной его части входят две группы железородиевых и платиновых термометров сопротивления. Каждая группа содержит два платиновых и два железородиевых термометра, постоянно находящихся в блоке сравнения — массивном цилиндре с четырьмя продольными каналами для термометров. Передача шкалы термометрам, вторичным и рабочим эталонам, осуществляется приведением их в тепловой контакт с эталонным блоком сравнения и сличением в криостате. Среднеквадратическая погрешность эталона лежит в пределах 0,3—1 мК, а неисключенная систематическая погрешность — в пределах 0,4—1,5 мК для любого значения температуры поддиапазона. Наименьшие значения соответствуют точке 0,8 К. В состав второго эталона входят платиновые термометры сопротивления, температурные лампы, аппаратура воспроизведения реперных точек в диапазоне 271,16-1355,77 К. Среднеквадратическая погрешность этого эталона лежит в пределах 5-Ю-5—I IO72; неиск- люченная систематическая погрешность — МО"4-5-Ю-3 (в относительных значениях). В английской и американской научной литературе иногда встречается абсолютная термодинамическая шкала шотландца У. Ранки- на (R), одного из создателей технической термодинамики. Ее нулевая точка совпадает с О К, а градус Ранкина (°R) по величине равен градусу Фаренгейта. Точка таяния льда 491,67°R, кипения воды 671,67°R. Перевод в температуру Кельвина выполняется по уравнению Тк = 5/9/R. До нашего времени из всего множества температурных шкал дошли всего четыре, хотя и это явно многовато. В науке температуру выражают в Кельвинах, а в жизни мы используем градусы Цельсия и изредка встречаем шкалы Реомюра и Фаренгейта. Выражения для взаимного перевода интервальных практических шкал Фаренгейта, Реомюра и Цельсия, включая и термодинамическую, можно представить в следующем виде: > шкала Цельсия: °С = 1 К; Т= + 273,15, где Т— температура Кельвина; /ц — температура Цельсия; > шкала Реомюра: l°Re = 1,25 °С; = 1,25/^, где tRe — температура Реомюра; Т— 1,25/Ке + 273,15; > шкала Фаренгейта: 1°F = 5/9 °С = 5/9 К; /ц = 5/Щ - 32), где /F — температура Фаренгейта; Т= 5/9(/р — 32) + 273,15. Соотношения между шкалами приведены в табл. 7.6. Следует иметь в виду, что, нагревая изолированное тело, можно суммировать приращение его термодинамической температуры. Например, тело было нагрето до 100 К, нагрели еще на 50 К, в итоге получили 150 К. Если температура кипения одной жидкости 100 К, а другой — 50 К, то справедливо утверждать, что первое значение в 2 раза больше второго. Но суммировать термодинамические температуры различных тел нельзя, это бессмысленно и равносильно известной шутке о средней температуре в больнице. Особенно осторожно следует поступать со шкалами Цельсия, Реомюра, Фаренгейта, поскольку они начинаются с условных нулей. Скажем, по Цельсию иногда можно найти среднее арифметическое значение, измерив температуру воздуха в разны
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 821; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.155.20 (0.014 с.) |

 2-.10 Н
2-.10 Н
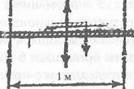


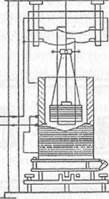

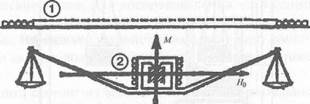 Рис. 7.12. Установка для «взвешивания» тока
Рис. 7.12. Установка для «взвешивания» тока

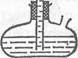
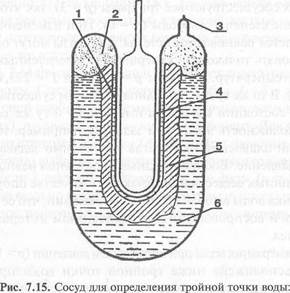 1 — слой воды; 2 — пар; 3 — место запайки сосуда; 4 — колба термометра;
5 — лед; 6 — вода
1 — слой воды; 2 — пар; 3 — место запайки сосуда; 4 — колба термометра;
5 — лед; 6 — вода




