
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерії оцінки виконання завдань лабораторних занятьСодержание книги Поиск на нашем сайте Критерії оцінки виконання завдань лабораторних занять з дисципліни «Оптимізаційні методи та моделі» для студентів ІІ курсу (освітньо-кваліфікаційний рівень —бакалавр) Оцінювання знань студента під час практичних занять проводиться за шкалою, визначеною кафедрою, за такими критеріями: · розуміння, ступінь засвоєння теорії завдань, що розв´язуються; · ступінь засвоєння фактичного матеріалу курсу; · уміння поєднувати теоретичні знання з вирішенням практичних завдань при розв’язанні задач, проведенні розрахунків тощо при виконанні завдань; · логіка, структура, стиль викладу матеріалу при виступах в аудиторії, уміння захищати свою позицію та здійснювати узагальнення інформації, отриманої з відповідей інших осіб.
Оцінка, еквівалентна «відмінно», виставляється, якщо студент виявив всебічно системні та глибокі знання, в повному обсязі твердо засвоїв весь програмний матеріал, вичерпно та послідовно дав відповіді на всі питання екзаменаційного білета, тісно пов’язує теорію з практикою, показує вміння самостійно аналізувати та тлумачити математичні поняття і застосовувати їх при вирішенні завдань, правильно аргументує висновки, вміє самостійно узагальнювати матеріал і логічно його викладати, не допускаючи помилок. Оцінка, еквівалентна «добре», виставляється, якщо студент твердо знає програмний матеріал, має навики аналізу та тлумачення математичних понять, логічно відповідає на поставлені питання, не допускає суттєвих помилок. Оцінка, еквівалентна «задовільно», виставляється, якщо студент засвоїв основний матеріал, але не знає окремих деталей, допускає неточні відповіді та формулювання понять, порушує послідовність у викладенні програмного матеріалу, має прогалини в знаннях. Оцінка, еквівалентна «незадовільно», виставляється, якщо студент не знає значної частини програмного матеріалу, допускає суттєві помилки, не володіє навичками застосування математичних понять, які забезпечували б вирішення завдань. Рівень знань студентів оцінюється за чотирибальною системою: Оцінка «5 (відмінно)» ставиться, коли навчальний матеріал засвоєно у повному обсязі, студент дає обґрунтовані, глибокі йтеоретично правильні розв'язки усіх завдань. Оцінка «4 (добре)» - студент володіє матеріалом, розв'язав усі завдання, але допустив окремі незначні помилки і неточності. На оцінку «3 (задовільно)» заслуговує студент, який володіє знаннями з дисципліни, але знання недостатньо глибокі, мають місце суттєві неточності, істотні помилки, відсутня послідовність і чіткість, розв'язано не менше 2/3 роботи. Оцінка «2 (незадовільно)» - матеріал студентом не засвоєний, в роботі допускаються грубі помилки, відсутні необхідні знання та уміння, розв'язано менше 2/3 роботи. Тема 1. Предмет, методи і завдання дисципліни. Класифікація задач.
ЛАБОРАТОРНЕ ЗАНЯТТЯ №1
Тема заняття: Розв’язування задач міжгалузевого балансу. Мета: сформувати вміння та навички розв’язування задач міжгалузевого балансу типу «витрати-випуск» з використанням вбудованих функцій програми Microsoft Excel.
Постановка задачі: 1. Використовуючи дані таблиці 1 «Витрати – випуск» обчислити: 1.1. коефіцієнти прямих, непрямих та повних витрат; 1.2. абсолютні та відносні прирости (падіння) валового випуску кожної галузі, якщо кінцеве споживання галузі І збільшиться на 2. За даними таблиці 2, яка для таблиці 1 відображає норми витрат ресурсів та відповідну їм вартість, визначити: 1. загальну витрату ресурсів на виконання виробничої програми; 2. коефіцієнти прямих витрат ресурсів на одиницю кінцевої продукції; 3. витрату ресурсів за галузями; 4. виробничі витрати в грошових одиницях по галузям і на всю виробничу програму; 5. виробничі витрати на одиницю кінцевої продукції.
Примітка: при обчисленнях скористатися вбудованими математичними функціями MS Excel: «СУММ» – для обчислення суми, «МУМНОЖ» – для обчислення добутку матриць, «МОБР» – для обчислення оберненої матриці.
Порядок розв’язання: Таблиця 1 ВИТРАТИ – ВИПУСК
де
Для обчислення коефіцієнтів прямих, непрямих та повних витрат визначимо: Валовий випуск кожної галузі за формулою: Матрицю прямих витрат, як: Матрицю непрямих витрат за формулою:
Для обчислення абсолютних та відносних приростів (падінь) валового випуску кожної галузі, якщо кінцеве споживання галузі І збільшиться на Валовий випуск, якщо кінцеве споживання галузі І збільшиться на Абсолютні прирости (падіння) за формулою: Відносні прирости, як: Таблиця 2 НОРМИ ВИТРАТ РЕСУРСІВ
де Загальну витрату ресурсів на виконання виробничої програми визначимо як:
Коефіцієнти прямих витрат ресурсів на одиницю кінцевої продукції визначимо як: Витрату ресурсів за галузями визначимо за формулою:
Виробничі витрати в грошових одиницях по галузям визначимо як: Виробничі витрати на одиницю кінцевої продукції визначимо як: Задача 1 1. Використовуючи дані таблиці 1 «Витрати – випуск» обчислити: 1.1. коефіцієнти прямих, непрямих та повних витрат; 1.2. абсолютні та відносні прирости (падіння) валового випуску кожної галузі, якщо кінцеве споживання галузі І збільшиться на 2. За даними таблиці 2, яка для таблиці 1 відображає норми витрат ресурсів та відповідну їм вартість, визначити: 2.1. загальну витрату ресурсів на виконання виробничої програми; 2.2. коефіцієнти прямих витрат ресурсів на одиницю кінцевої продукції; 2.3. витрату ресурсів за галузями; 2.4. виробничі витрати в грошових одиницях по галузям і на всю виробничу програму; 2.5. виробничі витрати на одиницю кінцевої продукції.
Примітка: при обчисленнях скористатися вбудованими математичними функціями MS Excel: «СУММ» – для обчислення суми, «МУМНОЖ» – для обчислення добутку матриць, «МОБР» – для обчислення оберненої матриці.
Таблиця 1 ВИТРАТИ – ВИПУСК
Таблиця 2 НОРМИ ВИТРАТ РЕСУРСІВ
ДОДАТКОВІ ЗАВДАННЯ: 1. Використовуючи дані таблиці 1 «Витрати – випуск» обчислити: 1.1. коефіцієнти прямих, непрямих та повних витрат; 1.2. абсолютні та відносні прирости (падіння) валового випуску кожної галузі, якщо кінцеве споживання галузі І збільшиться на 2. За даними таблиці 2, яка для таблиці 1 відображає норми витрат ресурсів та відповідну їм вартість, визначити: 2.1. загальну витрату ресурсів на виконання виробничої програми; 2.2. коефіцієнти прямих витрат ресурсів на одиницю кінцевої продукції; 2.6. витрату ресурсів за галузями; 2.7. виробничі витрати в грошових одиницях по галузям і на всю виробничу програму; 2.8. виробничі витрати на одиницю кінцевої продукції.
Примітка: при обчисленнях скористатися вбудованими математичними функціями MS Excel: «СУММ» – для обчислення суми, «МУМНОЖ» – для обчислення добутку матриць, «МОБР» – для обчислення оберненої матриці.
Таблиця 1 ВИТРАТИ – ВИПУСК
Таблиця 2 НОРМИ ВИТРАТ РЕСУРСІВ
ЛАБОРАТОРНЕ ЗАНЯТТЯ №2
Тема заняття: Класифікація та побудова математичних моделей економічних задач. Мета: сформувати навички класифікації та побудови математичних моделей економічних задач.
Задача 1. Невелика сімейна фірма виготовляє два види безалкогольних напоїв — "Pink Fizz" та "Mint Pop". Фірма має можливість реалізувати всю виготовлену продукцію, але об’єм виробництва обмежений кількістю головного компонента та потужністю виробничого обладнання. Для виготовлення 1 л напою "Pink Fizz" необхідно 0,02 години роботи обладнання, а для виготовлення 1 л напою "Mint Pop" — 0,04 години. Витрати головного компонента становлять 0,01 кг і 0,04 кг на 1 л напоїв "Pink Fizz" та "Mint Pop" відповідно. Щоденно фірма має можливість використовувати обладнання протягом 24 годин, та витрачати для приготування напоїв до 16 кг головного компонента. Прибуток фірми від реалізації 1 л напою "Pink Fizz" становить 0,1 у.о., а напою "Mint Pop" – 0,30 у.о. Побудувати математичну модель задачі, яка дозволить фірмі оптимізувати виробництво напоїв.
Задача 2. Необхідно знайти оптимальний розподіл землі площею 10 тис. га під пшеницю та картоплю за критерієм максимум прибутку. Економічні показники їх виробництва наведені у наступній таблиці:
Задача 3. Для виробництва двох видів продукції (А і В) підприємство використовує 4 вида ресурсів. Норми затрат ресурсів на виробництво одиниці продукції, об’єм ресурсів, а також прибуток від реалізації одиниці продукції наведені в таблиці:
Побудувати математичну модель задачі, яка дозволить визначити оптимальний план виробництва продукції, що забезпечить підприємству одержання максимального прибутку.
Задача 4. Для відгодівлі тварин використовують два види кормів А і В, які містять у певній кількості поживні речовини С1, С2 і С3. Відомо, скільки одиниць кожної поживної речовини міститься в 1 кг кожного корму, мінімальна добова потреба у кожній поживній речовині при відгодівлі тварин, а також вартість 1 кг корму, і наведено у таблиці:
Необхідно побудувати математичну модель задачі, яка дозволить скласти добовий раціон для відгодівлі тварин таким чином, щоб задовольнялася мінімальна добова потреба в поживних речовинах і загальна вартість раціону була б мінімальною.
Задача 5. Відомо, що за агротехнічними нормами на 1 га ґрунту, що обробляє фермерське господарство, потрібно вносити протягом сезону основні поживні речовини у кількості не менше за 6 од. фосфору, 8 од. азоту, 12 од. калію. Фермерське господарство має можливість придбати добрива складу А1, А2 та А3. В 1 кг добрива в залежності від складу містяться основні поживні речовини у кількості: А1: 2 од. Р, 1 од. N, 3 од. К А2: 1 од. Р, 2 од. N, 4 од. К А3: 3 од. Р, 1,5 од. N, 2 од. К Ціни за 1 кг добрива складають: А1 – 2 грн., А2 – 3,5 грн., А3 – 2,5 грн. Побудувати математичну модель задачі, яка дозволить скласти найбільш економічний план закупівлі добрив.
Задача 6. Для виготовлення трьох видів виробів І, ІІ, ІІІ мале підприємство використовує три типи устаткування, ресурс якого складає, відповідно, 360, 192 та 180 станко-годин. Від реалізації одиниці продукції І-го виду можна отримати прибуток 9 грн., ІІ-го – 10 грн., а ІІІ-го – 16 грн. Відома матриця технологічних коефіцієнтів
ДОДАТКОВІ ЗАВДАННЯ: №1: Кондитерська фабрика для виготовлення трьох видів пастили А, В, С використовує три основні види сировини: цукор, фруктове пюре та молоко. Норми витрат на виготовлення 1 т. пастили кожного типу приведені в таблиці:
Побудувати математичну модель задачі.
№2: Для виготовлення двох видів продукції Р1 та Р2 використовують три види сировини S1, S2, S3. Всі дані наведені у таблиці: \
Побудувати математичну модель задачі.
№3: Для виготовлення трьох видів продукції А, В, С використовують фрезувальне, токарне, зварювальне та шліфувальне обладнання. Витрати часу на обробку одного виду продукції та загальний фонд робочого часу для кожного типу обладнання наведені в таблиці:
Побудувати математичну модель задачі.
ЛАБОРАТОРНЕ ЗАНЯТТЯ №3
Тема заняття: Графічний метод розв’язання задач лінійного програмування. Мета: сформувати вміння та навички розв’язування задач лінійного програмування графічним методом.
Задача 1. Розв’язати задачу лінійного програмування графічним методом: 1.1.
1.3.
1.5.
1.7.
ДОДАТКОВІ ЗАВДАННЯ: №1: Розв’язати задачу лінійного програмування графічним методом: 1.1.
№2: Розв’язати графічним методом задачі, для яких побудована математична модель на попередньому практичному занятті (задачі №1, 2, 3, 4).
ЛАБОРАТОРНЕ ЗАНЯТТЯ №4
Тема заняття: Симплексний метод розв’язання задач лінійного програмування. Мета: сформувати вміння та навички розв’язування задач лінійного програмування симплексним методом.
Задача 1. Розв’язати задачу лінійного програмування симплексним методом: 1.1.
ДОДАТКОВІ ЗАВДАННЯ: №1: Розв’язати задачу лінійного програмування симплексним методом: 1.1.
№2: Розв’язати симплексним методом задачу, для якої побудована математична модель на другому практичному занятті (задача №6). ЛАБОРАТОРНЕ ЗАНЯТТЯ №5
Тема заняття: Симплексний метод розв’язання задач лінійного програмування. Мета: сформувати вміння та навички розв’язування задач лінійного програмування симплексним методом. Задача 1. Розв’язати задачу лінійного програмування симплексним методом: 1.1.
ДОДАТКОВІ ЗАВДАННЯ: №1: Розв’язати задачу лінійного програмування симплексним методом: 1.1.
ЛАБОРАТОРНЕ ЗАНЯТТЯ №6
Тема заняття: Розв’язання задач лінійного програмування методом штучного базису. Мета: сформувати вміння та навички розв’язування задач лінійного програмування методом штучного базису. Задача 1. Розв’язати задачу лінійного програмування методом штучного базису: 1.1.
1.3.
ДОДАТКОВІ ЗАВДАННЯ: №1: Розв’язати задачу лінійного програмування методом штучного базису: 1.1.
ЛАБОРАТОРНЕ ЗАНЯТТЯ №7
Тема заняття: Розв’язання задач лінійного програмування засобами програми Microsoft Excel. Мета: сформувати вміння та навички розв’язування задач лінійного програмування засобами програми Microsoft Excel. Задача 1. Розв’язати задачу лінійного програмування засобами програми Microsoft Excel: Невелика сімейна фірма виготовляє два види безалкогольних напоїв — "Pink Fizz" та "Mint Pop". Фірма має можливість реалізувати всю виготовлену продукцію, але об’єм виробництва обмежений кількістю головного компонента та потужністю виробничого обладнання. Для виготовлення 1 л напою "Pink Fizz" необхідно 0,02 години роботи обладнання, а для виготовлення 1 л напою "Mint Pop" — 0,04 години. Витрати головного компонента становлять 0,01 кг і 0,04 кг на 1 л напоїв "Pink Fizz" та "Mint Pop" відповідно. Щоденно фірма має можливість використовувати обладнання протягом 24 годин, та витрачати для приготування напоїв до 16 кг головного компонента. Прибуток фірми від реалізації 1 л напою "Pink Fizz" становить 0,1 у.о., а напою "Mint Pop" – 0,30 у.о. Розв’язати задачу при умові отримання фірмою максимального прибутку.
Задача 2. Розв’язати задачу лінійного програмування засобами програми Microsoft Excel: Необхідно знайти оптимальний розподіл землі площею 10 тис. га під пшеницю та картоплю за критерієм максимум прибутку. Економічні показники їх виробництва наведені у наступній таблиці:
Задача 3. Розв’язати задачу лінійного програмування засобами програми Microsoft Excel: Для виробництва двох видів продукції (А і В) підприємство використовує 4 види ресурсів. Норми затрат ресурсів на виробництво одиниці продукції, об’єм ресурсів, а також прибуток від реалізації одиниці продукції наведені в таблиці:
Розв’язати задачу за умови отримання підприємством максимального прибутку від реалізації готової продукції.
Задача 4. Розв’язати задачу лінійного програмування засобами програми Microsoft Excel: Для відгодівлі тварин використовують два види кормів А і В, які містять у певній кількості поживні речовини С1, С2 і С3. Відомо, скільки одиниць кожної поживної речовини міститься в 1 кг кожного корму, мінімальна добова потреба у кожній поживній речовині при відгодівлі тварин, а також вартість 1 кг корму, і наведено у таблиці:
Розв’язати задачу за умови отримання найбільш економічного плану закупівлі кормів.
Задача 5. Розв’язати задачу лінійного програмування засобами програми Microsoft Excel: Відомо, що за агротехнічними нормами на 1 га ґрунту, що обробляє фермерське господарство, потрібно вносити протягом сезону основні поживні речовини у кількості не менше за 6 од. фосфору, 8 од. азоту, 12 од. калію. Фермерське господарство має можливість придбати добрива складу А1, А2 та А3. В 1 кг добрива в залежності від складу містяться основні поживні речовини у кількості: А1: 2 од. Р, 1 од. N, 3 од. К А2: 1 од. Р, 2 од. N, 4 од. К А3: 3 од. Р, 1,5 од. N, 2 од. К Ціни за 1 кг добрива складають: А1 – 2 грн., А2 – 3,5 грн., А3 – 2,5 грн. Розв’язати задачу за умови отримання найбільш економічного плану закупівлі добрив фермерським господарством.
Задача 6. Розв’язати задачу лінійного програмування засобами програми Microsoft Excel: Для виготовлення трьох видів виробів І, ІІ, ІІІ мале підприємство використовує три типи устаткування, ресурс якого складає, відповідно, 360, 192 та 180 станко-годин. Від реалізації одиниці продукції І-го виду можна отримати прибуток 9 грн., ІІ-го – 10 грн., а ІІІ-го – 16 грн. Відома матриця технологічних коефіцієнтів
ДОДАТКОВІ ЗАВДАННЯ: №1: Розв’язати задачі лінійного програмування засобами програми Microsoft Excel: 1.1.
1.3.
Тема 3. Транспортна задача. ЛАБОРАТОРНЕ ЗАНЯТТЯ №8
Тема заняття: Побудова вихідних опорних планів транспортної задачі. Мета: сформувати вміння та навички побудови вихідних опорних планів транспортної задачі методами північно-західного кута, найменшої вартості та подвійного перевантаження. Задача 1. Скласти вихідний план транспортної задачі методами північно-західного кута, найменшої вартості та подвійного перевантаження і оцінити його вартість, якщо відомі:
1.
3. 5.
ДОДАТКОВІ ЗАВДАННЯ: 7. 9.
Тема 3. Транспортна задача. ЛАБОРАТОРНЕ ЗАНЯТТЯ №9
Тема заняття: Розв’язання транспортної задачі методом потенціалів. Мета: сформувати вміння та навички розв’язання транспортної задачі методом потенціалів.
Задача 1 Розв’язати методом потенціалів транспортну задачу: 1.1.
1.3.
ДОДАТКОВІ ЗАВДАННЯ: Задача 2 Розв’язати методом потенціалів транспортну задачу: 2.1.
Тема 3. Транспортна задача. ЛАБОРАТОРНЕ ЗАНЯТТЯ №10
Тема заняття: Розв’язання транспортної задачі методом потенціалів. Мета: сформувати вміння та навички розв’язання транспортної задачі методом потенціалів.
Задача 1 Розв’язати методом потенціалів транспортну задачу: 1.1. 1.2.
ДОДАТКОВІ ЗАВДАННЯ: Задача 2 Розв’язати методом потенціалів транспортну задачу: 2.1.
ЛАБОРАТОРНЕ ЗАНЯТТЯ №11
Тема заняття: Розв’язання взаємо-двоїстих задач. Мета: сформувати вміння й навички побудови та розв’язання двоїстих задач.
Розв’язати задачі лінійного програмування симплекс-методом та знайти рішення прямої та двоїстої задачі. До наведених задач записати двоїсту задачу до поставленої задачі лінійного програмування. Розв’язати одну з пари задач і за цим розв’язком визначити оптимальний план іншої задачі.
Задача 1
Задача 2
Задача 3
ДОДАТКОВІ ЗАВДАННЯ: Розв’язати задачі лінійного програмування симплекс-методом та знайти рішення прямої та двоїстої задачі. До наведених задач записати двоїсту задачу до поставленої задачі лінійного програмування. Розв’язати одну з пари задач і за цим розв’язком визначити оптимальний план іншої задачі. Задача 4
Задача 5
ЛАБОРАТОРНЕ ЗАНЯТТЯ №12
Тема заняття: Економічна інтерпретація двоїстих задач. Мета: сформувати вміння та навички економічної інтерпретації двоїстих задач.
Задача 1 Розв’язати задачу лінійного програмування симплекс-методом та зробити економічний аналіз: для виготовлення чотирьох видів продукції А,Б,В,Г використовуються три види сировини 1,2,3. Норми витрат усіх ресурсів на одиницю продукції запаси ресурсів, а також ціни на продукцію наведені в таблиці.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 265; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |

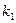 одиниць, а галузі ІІ - на
одиниць, а галузі ІІ - на 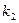 одиниць.
одиниць.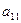

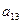
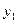

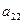
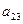
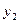
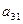


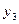
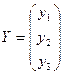 - матриця кінцевого споживання
- матриця кінцевого споживання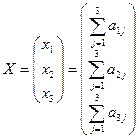 .
.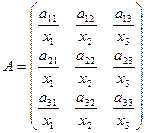 .
.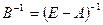 , де
, де 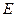 – одинична матриця
– одинична матриця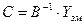 , де
, де 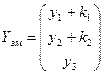 .
.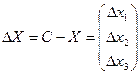 .
. .
.

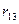
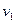
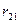
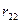
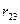

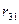
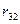
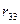

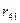
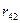
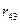
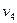
 - матриця норм витрат ресурсів.
- матриця норм витрат ресурсів.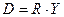
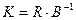
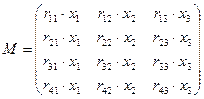
 .
.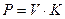 .
. одиниць, а галузі ІІ - на
одиниць, а галузі ІІ - на 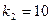 одиниць.
одиниць. 15
15
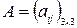 , де
, де  – кількість годин, яка потрібна для виготовлення одиниці
– кількість годин, яка потрібна для виготовлення одиниці 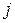 -го виробу на устаткуванні
-го виробу на устаткуванні 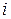 -го типу:
-го типу: 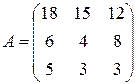 . Побудувати математичну модель задачі, яка дозволить скласти план використання устаткування, за яким підприємство отримає найбільший прибуток від реалізації готової продукції.
. Побудувати математичну модель задачі, яка дозволить скласти план використання устаткування, за яким підприємство отримає найбільший прибуток від реалізації готової продукції.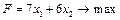 ; 1.2.
; 1.2. 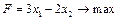 ;
;

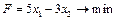 ; 1.4.
; 1.4. 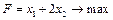 ;
;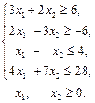

 ; 1.6.
; 1.6. 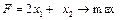 ;
;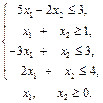
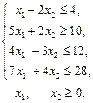
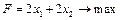 ; 1.8.
; 1.8.  ;
;
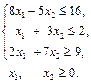
 ; 1.2.
; 1.2. 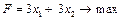 ;
;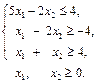
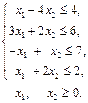
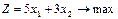 1.2.
1.2. 
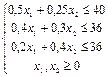
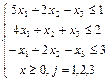
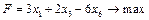 ;
;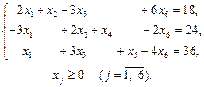
 ; 1.2.
; 1.2.  ;
;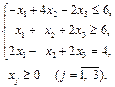
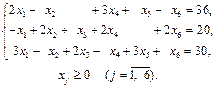
 ;
;
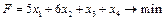 ; 1.2.
; 1.2. 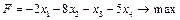 ;
;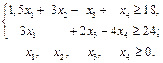

 ; 1.4.
; 1.4. 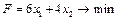 ;
;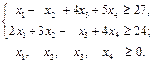
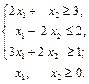
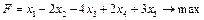 ; 1.2.
; 1.2.  ;
;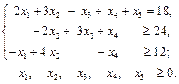
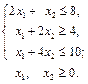
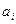 – запаси однотипної продукції торгівельних баз;
– запаси однотипної продукції торгівельних баз;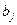 – величини попиту магазинів роздрібної торгівлі;
– величини попиту магазинів роздрібної торгівлі;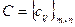 – вартість перевезення одиниці однотипної продукції від
– вартість перевезення одиниці однотипної продукції від 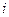 -ї торгівельної бази до
-ї торгівельної бази до 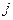 -го магазину роздрібної торгівлі.
-го магазину роздрібної торгівлі.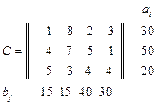 ; 2.
; 2. 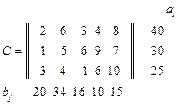 ;
;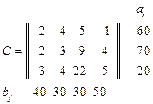 ; 4.
; 4.  ;
;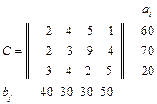 ; 6.
; 6. 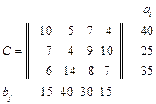 ;
; ; 8.
; 8.  ;
;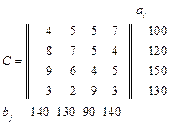 ; 10.
; 10. 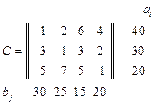 ;
; ,
,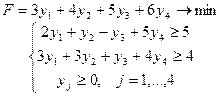 ,
, .
.




