
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сила тяги электромагнита постоянного тока.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для оценки эффективности электромагнитов очень важно знать величину силы, действующий на подвижный якорь и динамику ее изменения. Эту силу принято называть силой тяги, а зависимость силы тяги от воздушного зазора δ при неизменном токе в обмотке - статической тяговой характеристикой электромагнита. Получим выражение для тягового усилия в электромагните постоянного тока. Исходя из закона сохранения энергии, можно сказать, что энергия, полученная электромагнитом, равна сумме энергии потерь в активном сопротивлении цепи и энергии, затраченной на создание магнитного поля:
- энергия, сообщенная электромагниту (работа источника, затраченная на изменение потокосцепления катушки). Вместе с тем, энергия, полученная магнитным полем при элементарном перемещении якоря, определяется механической работой, произведенной якорем, и изменениями запаса электромагнитной энергии:
где, i dΨ - элементарная энергия, полученная полем при перемещении якоря; Р dx - элементарная работа, произведенная якорем; dWm - приращение магнитной энергии. Из (6) следует:
Учитывая, что элементарное перемещение dx = - dδ (воздушный зазор уменьшается) и Wm = (1/2) iΨ, получим для ненасыщенной магнитной системы электромагнита:
С учетом того, что для электромагнитов постоянного тока ток i при элементарном перемещении dδ не меняется, выражение (8) для тягового усилия представляется в виде:
Рассмотрим расчет силы тяги для электромагнита с двумя рабочими зазорами. Полное потокосцепление складывается из рабочего потокосцепления Ψδ и потока рассеяния Ψσ. Поскольку ненасыщенная магнитная цепь линейна, потокосцепление:
где, F = I.w - М.Д.С. обмотки электромагнита; λδ - магнитная проводимость воздушного зазора. Потокосцепление рассеяния:
где, λσ - магнитная проводимость пути потока рассеяния; l - длина пути потока рассеяния. Подставив (10) и (11) в (9) получим:
Поскольку проводимость λσ от зазора не зависит, то d(l λσ) / dδ = 0 и сила тяги электромагнита:
Если известна зависимость λδ = f(δ), то d λδ / d δ находится аналитически. Если λδ определяется в результате построения картины поля, то производится расчет λδ для ряда положений якоря электромагнита, после чего строится зависимость λδ = f(δ), и производится графическое дифференцирование. При достаточно малом зазоре (рис. 11.1а) можно считать:
где, S - сечение воздушного зазора. Тогда сила тяги электромагнита:
Сила тяги электромагнита при одном рабочем зазоре и той же М.Д.С.
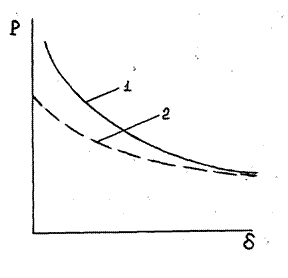
Таким образом, при одной и той же М.Д.С. сила тяги электромагнита с одним рабочим зазором в два раза больше, чем при двух зазорах. Согласно (13) сила тяги пропорциональна квадрату М.Д.С. обмотки, площади полюса и обратно пропорциональна квадрату размера зазора. Зависимость Р = f(δ) при неизменной М.Д.С., называют статической тяговой характеристикой, она представлена на (рис. 3) (кривая 1).
Рис. 3. Статические тяговые характеристика электромагнита.
По мере уменьшения δ сила тяги резко возрастает и при δ = 0 стремится к бесконечности. В действительности при δ → 0 возрастает магнитный поток и увеличивается падение магнитного потенциала в магнитопроводе, причем только часть М.Д.С. оказывается приложеноной к воздушному зазору. Зависимость Р = f(δ) может быть получена из формулы Максвелла:
где, Вδ - индукция в рабочем зазоре; S - сечение сердечника. Так как при δ = 0 вся М.Д.С. тратится на проведение магнитного потока по стали магнитопровода, то напряженность магнитного поля Н = F / lст. Индукция В при этом может быть найдена по кривой намагничивания, а сила по выражению (15) и имеет конечное значение. На (рис. 2) кривая 2 изображает зависимость Р = f(δ), снятую экспериментально. Многочисленные исследования показали, что для расчета силы тяги можно пользоваться (11.12). При этом вместо F подставляется падение магнитного потенциала Fδ:
Значение Fδ находят в результате расчета магнитной цепи.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 445; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.130.242 (0.009 с.) |




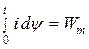 где, - энергия, поступающая из сети; - потери энергии в катушке электромагнита;
где, - энергия, поступающая из сети; - потери энергии в катушке электромагнита; (6)
(6) (7)
(7) (8)
(8) (9)
(9) (10)
(10) (11)
(11)
 (12)
(12)
 - магнитная проницаемость воздушного зазора;
- магнитная проницаемость воздушного зазора; (13)
(13) (14)
(14)
 (15)
(15) (16)
(16)


