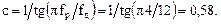Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика проектування рекурсивних ЦФ на основі білінійного z – перетворення аналогового фільтра-прототипуСодержание книги
Поиск на нашем сайте
Проектування ЦФ за аналоговим прототипом включає в себе такі етапи: - вибір виду апроксимації і розрахунок параметрів функції, що апроксимується; - розрахунок порядку аналогового фільтра-прототипу; - розрахунок передавальної функції аналогового фільтра-прототипу; - розрахунок передавальної функції ЦФ. На рис. 3.12 зображені види апроксимуючих функцій ана
Рис. 3.12. Апроксимуючі функції аналогових фільтрів-прототипів: смузі затримання
де Як правило, спочатку розглядається нормована АЧХ НЧ з
При Представимо методику синтезу ЦФ за аналоговим прототипом, яким є фільтр Баттерворта. В загальному випадку передавальна функція ФНЧ Баттерворта N – порядку Н(р) = 1 / BN(p), (3.6) де ВN(Р) – поліноми ступеня N з коренями в точках:
Вираз функції BN(p) для N=1 BN(p) = p + l; N=2 BN(p) = p2 + l,41p + l; N=3 BN(p) = (p + i) (p2 + P + i); N=4 BN(p) = (p2 + 0,7654p + l) (p2 + l,8478p +l); N=5 BN(p) = (p + l) (p2 + 0,6180p + l) (p2 + l,6180p + l). На практиці порядок фільтра Баттерворта розраховують відповідно до умови забезпечення певного рівня АЧХ 1/А на деякій заданій (як правило N = lgД/21g де Чим вище порядок фільтра (ступінь полінома), тим крутіші скати АЧХ від частоти зрізу fp до частоти заданого гарантованого придушення fs. Використовуючи рівність (3.6), представимо вираз для передавальних функцій нормованих (з частотою зрізу Н(р)1 = 1/(1 + р); Н(р)2 = l/(l + Н(р)3 = 1/(1 + 2р + 2p2 + р3). (3.8) Для перетворення нормованого фільтра НЧ на інший фільтр, найчастіше застосовують перетворення:
Тоді для передавальних функцій ФНЧ першого-третього порядків з довільною частотою H(p)1 = l/(l + p/ Н(р)3 = 1/[l +2 (p/ Якщо частота зрізу синтезованого ЦФ дорівнює
де
де Підставляючи рівність (3.10) в (3.9), після нескладних перетворень отримаємо вирази передавальних функцій ЦФ, подібних до аналогових ФНЧ Баттерворта першого-третього порядків:
де
де
де
Квадрат АЧХ аналогового ФНЧ Баттерворта
Квадрат АЧХ ЦФ
де H*(Z) – комплексно-спряжена передавальна функція; Rе і Im –дійсна та уявна частини АЧХ фільтра. Вираз (3.12) після заміни
де d0 = 20 (l + c3); d1 = 30 (l – c6); d2 = 12 (l + c6); d3 = 2 (l – c6). Практична реалізація ланок високого порядку, як правило, забезпечується за допомогою каскадного (послідовного) і (або) паралельного з'єднання ланок першого, другого і третього порядків. Як приклад розглянемо задачу визначення передавальної функції цифрового ФНЧ з монотонно спадною АЧХ (аналоговий прототип – фільтр Баттерворта). Задаються такі параметри фільтра: частота зрізу fp = 4 кГц, гранична частота смуги затримання fs = 8 кГц, нерівномірність АЧХ у смузі пропускання Порядок фільтра визначається відповідно до відношення (3.7):
і округляється до двох. Передавальна функція нормованого аналогового фільтра Баттерворта НЧ другого порядку (3.8) має вигляд Н(р)2 = 1/(1 + Після заміни Застосуємо білінійне Z-перетворення:
де Коефіцієнти у виразі H(Z)2 будуть:
де
Функціональна схема розрахованого рекурсивного цифрового ФНЧ другого порядку зображена на рис. 3.13.
Рис. 3.13. Функціональна схема цифрового ФНЧ другого порядку
Амплітудно-частотну характеристику фільтра знаходять згідно з виразом (3.12).
Цифрові системи АРП. Розглянуті нижче цифрові системи можуть бути використані при проектуванні ППОС систем електрозв¢язку та радіонавігаціі.
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.61.142 (0.007 с.) |

 так і в
так і в
 – нерівномірність АЧХ в смузі пропускання;
– нерівномірність АЧХ в смузі пропускання;  – нерівномірність АЧХ в смузі затримання (
– нерівномірність АЧХ в смузі затримання ( Апроксимація за Чебишевим дає АЧХ з рівновеликими пульсаціями в смузі пропускання і гладку АЧХ – в смузі затримання. Перехідна смуга
Апроксимація за Чебишевим дає АЧХ з рівновеликими пульсаціями в смузі пропускання і гладку АЧХ – в смузі затримання. Перехідна смуга  при цьому більш вузька, ніж при апроксимації за Баттервортом. Апроксимація за Кауером дає АЧХ з пульсаціями як в смузі пропускання, так і в смузі затримання, а ширина перехідної смуги виходить найменшою. Амплітудно-частотна характеристика задається на інтервалі зміни цифрових частот
при цьому більш вузька, ніж при апроксимації за Баттервортом. Апроксимація за Кауером дає АЧХ з пульсаціями як в смузі пропускання, так і в смузі затримання, а ширина перехідної смуги виходить найменшою. Амплітудно-частотна характеристика задається на інтервалі зміни цифрових частот  (
( – частота дискретизації) або
– частота дискретизації) або  , тому що вона симетрична відносно частоти
, тому що вона симетрична відносно частоти  або
або  . Апроксимація частотної характеристики фільтра грунтується на представленні квадрата модуля його АЧХ:
. Апроксимація частотної характеристики фільтра грунтується на представленні квадрата модуля його АЧХ:
 – загасання АЧХ на межі смуги пропускання
– загасання АЧХ на межі смуги пропускання  ;
;  – апроксимуюча функція порядку N;
– апроксимуюча функція порядку N;  ).
). , а потім здійснюється її частотне перетворення. В цьому випадку
, а потім здійснюється її частотне перетворення. В цьому випадку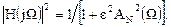
 (
( – гранична частота смуги затримання) придушення дорівнює А2. Параметри апроксимуючої функції розраховуються на основі вимог до АЧХ ЦФ, які задаються за допомогою величин fp, fs,
– гранична частота смуги затримання) придушення дорівнює А2. Параметри апроксимуючої функції розраховуються на основі вимог до АЧХ ЦФ, які задаються за допомогою величин fp, fs, 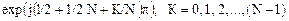 .
.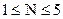 :
: .
. ) фільтрів Баттерворта (обмежимося значенням N від 1 до 3):
) фільтрів Баттерворта (обмежимося значенням N від 1 до 3): p + p2);
p + p2); – ФВЧ на ФНЧ,
– ФВЧ на ФНЧ,  – ФНЧ на ФВЧ.
– ФНЧ на ФВЧ.
 – частота дискретизації. Оскільки при Z–перетворенні відбувається заміна
– частота дискретизації. Оскільки при Z–перетворенні відбувається заміна  , то виникає
, то виникає , (3.10)
, (3.10)
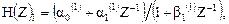

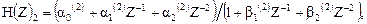


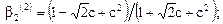
 (3.11)
(3.11)




 (3.12)
(3.12)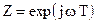 , наприклад, для ЦФ третього порядку рівняння (3.11) отримує вигляд
, наприклад, для ЦФ третього порядку рівняння (3.11) отримує вигляд ,
,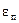 =1,6 дБ, гарантоване затухання в смузі затримання
=1,6 дБ, гарантоване затухання в смузі затримання 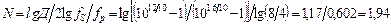
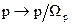 H(p)2 = l/[l +
H(p)2 = l/[l +