
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цифрова обробка радіонавігаційних сигналівСодержание книги
Поиск на нашем сайте
Нижче наведена методика розрахунку цифрових фільтрів може бути використана при проектуванні післядетекторних фільтрів 90 Гц і 150 Гц радіонавігаційних бортових приймачів ГРП та КРП. Відомо, що цифрова і аналогова обробки сигналів можливі у часовій або частотній областях. У першому випадку, наприклад, послідовність відліків вхідної часової функції UBX(t) після АЦП надходить на цифровий корелятор, на виході якого безпосередньо отримують відліки вихідної часової функції UBИX(t). У другому випадку швидким перетворенням Фур'є (ШПФ) із послідовності відліків ділянки вхідного процесу отримують послідовність відліків його спектральної функції, яку перемножують з відліками дискретизованої передавальної функції На практиці як елементи затримки застосовують регістри зсуву, які керуються імпульсами з частотою слідування Fд. Перемноження відліків, які знімаються з комірок регістрів, на ak, bi та підсумовування можна виконати за допомогою апаратних або програмних засобів. Для кола, зображеного на рис. 3.11,а в момент nТд відлік у точці А має вигляд
а вихідний відлік–
Передавальну функцію фільтра можна знайти як відношення перетворення Лапласа вихідного і вхідного сигналів
Нагадаємо, що перетворенням Лапласа безперервної функції
Перетворення Лапласа для дискретних вхідної та вихідної послідовностей буде:
Передавальна функція фільтра Використання передавальної функції в формулі (3.3) для аналізу дискретних кіл високого порядку досить складне, тому замість змінної р в функції ерТд вводять нову змінну Z (метод білінійного Z – перетворення), пов'язану з р співвідношеннями
З урахуванням останніх замін передавальна функція ЦФ
Якщо підставити замість Z = ерТд і прирівняти p до
Передавальна функція ЦФ подібна передавальній функції аналогового фільтра, проте вона внаслідок дискретизації повторюється на осі частот з періодом ТД=1/FД (рис. 3.11,б). Підбором коефіцієнтів аk і bi розташовують полюси та нулі в передавальній функції (3.5) таким чином, щоб отримати потрібну АЧХ фільтра. Отже, зображення передавальної функції у вигляді дробово-раціональної функції від комплексної змінної Z формула (3.4) дозволяє безпосередньо перейти до структури ЦФ. Тому при синтезі ЦФ слід апроксимувати передавальні функції аналогових фільтрів-прототипів К(р) дробово-раціональними функціями K(Z). Необхідно відмітити, що при білінійному Z – перетворенні співвідношення між частотами аналогового фільтра
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.208.243 (0.009 с.) |

 фільтра. В результаті отримують дискретизовану спектральну функцію вихідного процесу, потім зворотним ШПФ знаходять відліки вихідної функції UВИХ(t). Розробка алгоритмів ШПФ дозволила ефективно застосувати у практиці цифрової обробки сигналів спектральні перетворення, оскільки у порівнянні з дискретним перетворенням Фур'є в N/log2N разів скорочується час обчислення (N/2 відліків) спектральної функції S(j
фільтра. В результаті отримують дискретизовану спектральну функцію вихідного процесу, потім зворотним ШПФ знаходять відліки вихідної функції UВИХ(t). Розробка алгоритмів ШПФ дозволила ефективно застосувати у практиці цифрової обробки сигналів спектральні перетворення, оскільки у порівнянні з дискретним перетворенням Фур'є в N/log2N разів скорочується час обчислення (N/2 відліків) спектральної функції S(j  ) ділянки реалізації процесу UBX(t) за його N відліками. Оскільки в результаті дискретизації вхідного процесу його спектральна функція S(j
) ділянки реалізації процесу UBX(t) за його N відліками. Оскільки в результаті дискретизації вхідного процесу його спектральна функція S(j  може зумовити додаткові помилки, які пов'язані зі зміною процесу, що дискретизується, за час взяття відліку. Тому швидкодію АЦП потрібно вибирати, виходячи не з ширини спектра
може зумовити додаткові помилки, які пов'язані зі зміною процесу, що дискретизується, за час взяття відліку. Тому швидкодію АЦП потрібно вибирати, виходячи не з ширини спектра  , а з верхньої частоти
, а з верхньої частоти 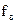 вузькосмужного процесу. Отже, в ЦФ вхідна послідовність чисел
вузькосмужного процесу. Отже, в ЦФ вхідна послідовність чисел  або просто Х(n), де ТД=1/FД – період дискретизації, за заданим алгоритмом перетворюється у вихідну послідовність Y(n). Цифрові фільтри можуть бути нерекурсивними та рекурсивними. В нерекурсивних фільтрах вихідні відліки Y(nTД) залежать тільки від зважених вхідних ak, bі = 0; в рекурсивних фільтрах вихідні відліки Y(nТд) залежать від зважених вхідних ak та зважених вихідних bi (рис. 3.11).
або просто Х(n), де ТД=1/FД – період дискретизації, за заданим алгоритмом перетворюється у вихідну послідовність Y(n). Цифрові фільтри можуть бути нерекурсивними та рекурсивними. В нерекурсивних фільтрах вихідні відліки Y(nTД) залежать тільки від зважених вхідних ak, bі = 0; в рекурсивних фільтрах вихідні відліки Y(nТд) залежать від зважених вхідних ak та зважених вихідних bi (рис. 3.11).



 – суматори; a k і b i; – вагові множники; Тд – елементи затримки на один крок дискретизації.
– суматори; a k і b i; – вагові множники; Тд – елементи затримки на один крок дискретизації.
 .
. є функція
є функція (3.1)
(3.1) (3.2)
(3.2) . (3.3)
. (3.3)
 . (3.4)
. (3.4)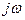 , то отримаємо:
, то отримаємо: . (3.5)
. (3.5) і ЦФ
і ЦФ  є істотно нелінійними, тому що при заміні
є істотно нелінійними, тому що при заміні  і
і  отримаємо:
отримаємо: 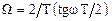 Але цю нелінійність перетворення для ЦФ верхніх і нижніх частот смугових і режекторних фільтрів легко компенсувати за допомогою корегуючих множників. Це робить білінійне Z – перетворення єдиним методом, придатним для проектування усіх чотирьох вказаних типів ЦФ. Крім цього, як прототипи можна в усіх випадках використовувати нормовані (з частотою зрізу
Але цю нелінійність перетворення для ЦФ верхніх і нижніх частот смугових і режекторних фільтрів легко компенсувати за допомогою корегуючих множників. Це робить білінійне Z – перетворення єдиним методом, придатним для проектування усіх чотирьох вказаних типів ЦФ. Крім цього, як прототипи можна в усіх випадках використовувати нормовані (з частотою зрізу 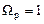 ) аналогові фільтри НЧ, для яких є таблиці передавальних функцій.
) аналогові фільтри НЧ, для яких є таблиці передавальних функцій.


