
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие развития числа. Действия над действительными числами.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Понятие развития числа. Действия над действительными числами. Развитие числа - увеличение его разрядности в направлении движения единиц по разрядам числа. a+b = b + a — коммутативность сложения; (a + b) + с = а + (b + с) — ассоциативность сложения; ab = ba — коммутативность умножения; (ab)c = а(Ьс) — ассоциативность умножения; a(b + c) = ab + ас — дистрибутивность умножения отноcительно сложения. А также выполняются следующие тождества: а + 0= a; а * 1 = а; a + (-a) = 0, 2 ВОПРОС Абсолютная и относительная погрешность. относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения. Абсолютной погрешностью приближенного значения называется модуль разности точного и приближенного значений. 3 ВОПРОС Линейные уравнения с одной переменной. Уравнением с одной переменной, называется равенство, содержащее только одну переменную. Уравнение вида ax = b, называется линейным. 4 ВОПРОС Квадратные уравнения. Уравнения, приводимые к квадратным. Квадра́тное уравне́ние — алгебраическое уравнение общего вида
где Выражение Биквадратные уравнения - происходит замена переменной. Рациональные уравнения – привести дробь к общему знаменателю, решить полученное целое уравнение. 5 ВОПРОС Системы линейных уравнений и системы уравнений второй степени. Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:
Система уравнений второй степени – это система уравнений, в которой есть хотя бы одно уравнение второй степени. 6 ВОПРОС Определитель второго и третьего порядков. Определителем второго порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом: Определителем третьего порядка называется число, определяемое с помощью элементов квадратной матрицы 3-го порядка следующим образом:
7 ВОПРОС Решение систем линейных уравнений с n неизвестными по формулам Крамера. Метод Крамера (формулы Крамера) — способ решения систем линейных уравнений, у которых количество переменных равно количеству уравнений. Применение метода Крамера возможно, если определитель, составленный из коэффициентов при переменных, не равен нулю. ВОПРОС Линейные неравенства, системы линейных неравенств. Различают два типа линейных неравенств: 1) Строгие неравенства: 2) Нестрогие неравенства:
Системой линейных неравенств называется любая совокупность двух или более линейных неравенств, содержащих одну и ту же неизвестную величину. 9 ВОПРОС Квадратные неравенства(метод интервала). Рациональные неравенства. Под квадратным неравенством понимается неравенство, которое может быть приведено к одному из следующих неравенств: ax2+bx+c>0, ax2+bx+c<0, ax2+bx+c≥0, ax2+bx+c≤0,
рациональным неравенством с одной переменной называют неравенство вида h (x) > q (x), где h (x) и q (x) – рациональные выражения, т.е. выражения, составленные из чисел и переменной x с помощью операций сложения, умножения, деления и возведения в натуральную степень (разумеется, переменная может быть обозначена любой другой буквой). 10 ВОПРОС Иррациональные уравнения. Иррациональные неравенства. Уравнения, содержащие неизвестную под знаком радикала называются иррациональными уравнениями. Например
Неравенство, содержащее неизвестные величины или некоторые функциии неизвестных величин под знаком радикала называется иррациональным неравенством. 11 ВОПРОС Уравнения с модулем. Уравнением с модулем называют равенство, содержащее переменную под знаком модуля. ВОПРОС Функция О.О.Ф. и М.З.Ф. Способы задания функции. График функции. Областью определения функции Множество значений функции – это все значения, которые принимает функция на своей области определения. СПОСОБЫ ЗАДАНИЯ: Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством. Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим. График функции — множество точек, у которых абсциссы являются допустимыми значениями аргумента 13 ВОПРОС ВОПРОС Преобразование графика функции: сдвиг, растяжение и сжатие вдоль осей координат.
ВОПРОС Обратная функция. Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. 16 ВОПРОС Сложная функция. Сложная функция – это функция, аргументом которой также является функция. 17 ВОПРОС ВОПРОС ВОПРОС ВОПРОС Показательные уравнения. Показательным уравнением называется уравнение, в котором неизвестная входит только в показатели степеней при некоторых постоянных основаниях. Простейшим показательным уравнением, решение которого сводятся к решению алгебраического уравнения, является уравнение вида af(x)=b,
ВОПРОС Показательные неравенства. Простейшим показательным неравенством является неравенство вида ax>b (1)
22 ВОПРОС ВОПРОС ВОПРОС ВОПРОС Логарифмические уравнения. Логарифмические уравнения — это уравнения, содержащие неизвестное под знаком логарифма и (или) в его основании. 29 ВОПРОС ВОПРОС Чётность, нечётность тригонометрических функций. 1. Область определения данной функции должна быть симметрична относительно точки О. То есть если некоторая точка a принадлежит области определения функции, то соответствующая точка -a тоже должна принадлежать области определения заданной функции. 2. Значение функции в точке х, принадлежащей области определения функции должно равняться значению функции в точке -х. То есть для любой точки х, из области определения функции должно выполняться следующее равенство f(x) = f(-x). Если построить график четной функции, он будет симметричен относительно оси Оу. Функция y=f(x) называется нечетной, если она удовлетворяет следующим двум условиям: 1. Область определения данной функции должна быть симметрична относительно точки О. То есть если некоторая точка a принадлежит области определения функции, то соответствующая точка -a тоже должна принадлежать области определения заданной функции. 2. Для любой точки х, из области определения функции должно выполняться следующее равенство f(x) = -f(x). График нечетной функции симметричен относительно точки О – начала координат. ВОПРОС ВОПРОС Формулы сложения.
37 ВОПРОС ВОПРОС Формулы приведения.
39 ВОПРОС Формулы преобразования суммы и разности тригонометрических функций в произведение. Сумма синусов есть удвоенное произведение синуса полусуммы на косинус полуразности:
Разность синусов есть удвоенное произведение синуса полуразности на косинус полусуммы:
Сумма косинусов есть удвоенное произведение косинуса полусуммы на косинус полуразности:
Разность синусов есть удвоенное произведение синуса полусуммы на синус полуразности, взятое со знаком минус:
Сумма тангенсов есть отношение синуса суммы к произведению косинусов:
Разность тангенсов есть отношение синуса разности к произведению косинусов:
Сумма котангенсов есть отношение синуса суммы к произведению синусов:
Разность котангенсов есть отношение синуса разности первого угла от второго к произведению синусов:
Для одного угла: Сумма косинуса и синуса:
Разность косинуса и синуса:
Сумма тангенса и котангенса:
С коэффициентами a и b:
ВОПРОС Основное соотношение
41 ВОПРОС ВОПРОС ВОПРОС Понятие развития числа. Действия над действительными числами. Развитие числа - увеличение его разрядности в направлении движения единиц по разрядам числа. a+b = b + a — коммутативность сложения; (a + b) + с = а + (b + с) — ассоциативность сложения; ab = ba — коммутативность умножения; (ab)c = а(Ьс) — ассоциативность умножения; a(b + c) = ab + ас — дистрибутивность умножения отноcительно сложения. А также выполняются следующие тождества: а + 0= a; а * 1 = а; a + (-a) = 0, 2 ВОПРОС
|
||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 2032; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.012 с.) |


 — свободная переменная,
— свободная переменная,  ,
,  ,
,  — коэффициенты, причём
— коэффициенты, причём 
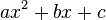 называют квадратным трёхчленом.
называют квадратным трёхчленом.
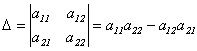 .
.
 .
. .
.
 (выражения f(x)) называют множество всех значений x, для которых функция (выражение) имеет смысл.
(выражения f(x)) называют множество всех значений x, для которых функция (выражение) имеет смысл. Функция y=f(x) называется четной, если она удовлетворяет следующим двум условиям:
Функция y=f(x) называется четной, если она удовлетворяет следующим двум условиям: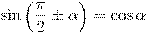 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
.



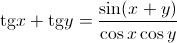








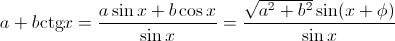
 ,
, 





