
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные формулы и законы механикиСодержание книги Поиск на нашем сайте
Кинематика Средняя скорость материальной точки: где Средняя путевая скорость: где ∆ S – длина пути; Мгновенная скорость материальной точки: где Модуль скорости материальной точки: Среднее ускорение материальной точки: Мгновенное ускорение материальной точки: Кинематическое уравнение равнопеременного движения материальной точки (
Скорость материальной точки при равнопеременном движении: При равномерном движении
При криволинейном движении ускорение материальной точки можно представить как векторную сумму нормальной Средняя угловая скорость материальной точки: Мгновенная угловая скорость материальной точки: Среднее угловое ускорение материальной точки: где Мгновенное угловое ускорение материальной точки: Кинематическое уравнение равномерного вращения материальной точки: Кинематическое уравнение равнопеременного вращения ( Модуль угловой скорости материальной точки при равнопеременном вращении: Связи между линейными и угловыми величинами, характеризующими вращение материальной точки по окружности радиуса R, выражается формулами:
Динамика материальной точки и тела, движущегося поступательно Уравнение движения материальной точки (второй закон Ньютона) в векторной форме:
где При Третий закон Ньютона:
Сила упругости:
Сила гравитационного взаимодействия двух тел: где Сила трения скольжения: Закон сохранения импульса замкнутой системы тел:
Работа, совершаемая постоянной силой где Работа, совершаемая переменной силой: При этом интегрирование проводится вдоль траектории, обозначаемой L. Средняя мощность, развиваемая силой в течение времени Мгновенная мощность: где α – угол между векторами силы Кинетическая энергия материальной точки (или тела, движущегося поступательно):
Потенциальная энергия упругодеформированного тела (сжатой или растянутой пружины): где k – коэффициент упругости и x – изменение длины тела. Потенциальная энергия гравитационного взаимодействия двух материальных точек (двух тел) массами
Потенциальная энергия тела, находящегося в однородном поле силы тяжести, на высоте h: П =mgh, где g – ускорение свободного падения тела. В замкнутой системе тел, в которой действуют только консервативные силы, полная механическая энергия этих тел является постоянной величиной: E= Т+П= const. Из законов сохранения энергии и импульса следует, что после прямого центрального удара двух шаров скорость абсолютно неупругих шаров равна
а скорости абсолютно упругих шаров равны
где Механика твёрдого тела Момент силы где Модуль момента силы где Момент инерции материальной точки относительно оси вращения: где m – масса точки, Момент инерции твердого тела относительно оси: где Момент инерции твердого тела в интегральной форме: Момент инерции стержня относительно оси, перпендикулярной стержню и проходящей через его середину:
Момент инерции стержня относительно оси, перпендикулярной стержню и проходящей через его конец: Момент инерции кольца (обруча) относительно оси, перпендикулярной плоскости кольца (обруча) и проходящей через его центр: где m – масса кольца (обруча) и R – его радиус. Момент инерции круглого однородного диска (цилиндра) относительно его оси симметрии: где m – масса диска (цилиндра) и Момент инерции однородного шара относительно его оси симметрии: где m – масса шара и По теореме Штейнера момент инерции тела относительно произвольной оси равен
где Момент импульса вращающегося тела относительно неподвижной оси:
где Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси:
где Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси в случае постоянного момента инерции:
где Закон сохранения момента импульса для замкнутой системы тел, момент инерции которой меняется относительно неподвижной оси:
где Закон сохранения момента импульса для двух взаимодействующих тел относительно неподвижной оси:
где Элементарная работа постоянного момента силы Мгновенная мощность, развиваемая моментом силы при вращении тела:
Кинетическая энергия вращающегося тела: где Кинетическая энергия тела, катящегося по плоскости без скольжения:
где Работа силы, совершаемая при вращении тела, расходуется на изменение его кинетической энергии:
где Относительное продольное растяжение (сжатие) тела: где Напряжение деформации тела: где F -модуль силы, действующей на площадь S поперечного сечения тела. Закон Гука для малой деформации тела: Потенциальная энергия упругого растянутого (сжатого) стержня:
где Механические колебания Уравнение гармонических колебаний точки вдоль оси Ox:
где A - амплитуда колебаний; Циклическая частота колебаний:
где Скорость точки, совершающей гармонические колебания вдоль оси Ox:
Ускорение точки, совершающей гармонические колебания вдоль оси Ox:
Амплитуда
определяется по формуле
где Начальная фаза
Уравнение траектории точки, участвующей в двух взаимно перпендикулярных гармонических колебаниях с амплитудами
Если начальные фазы
Дифференциальное уравнение гармонических колебаний материальной точки, на которую действует упругая сила
где Кинетическая энергия материальной точки, совершающей гармонические колебания:
Потенциальная энергия материальной точки, совершающей гармонические колебания:
Полная энергия материальной точки, совершающей гармонические колебания:
Период колебаний пружинного маятника: где Период колебаний математического маятника: где Период колебаний физического маятника: где Дифференциальное уравнение затухающих колебаний пружинного маятника:
где Решение дифференциального уравнения затухающих колебаний:
где Циклическая частота затухающих колебаний: Логарифмический декремент затухания: где Дифференциальное уравнение вынужденных колебаний:
где
Амплитуда вынужденных колебаний:
Резонансная частота и резонансная амплитуда:
Волновые процессы
Длина гармонической волны: где Для всех типов волн скорость их распространения: где Уравнение плоской гармонической волны, распространяющейся вдоль положительного направления оси где Скорость колеблющейся частицы в гармонической волне:
Ускорение колеблющейся частицы в гармонической волне:
Две волны называются когерентными, если разность их фаз остается постоянной во времени: Когерентные волны имеют одинаковые частоты и длины:
При наложении в пространстве двух когерентных волн происходит увеличение или уменьшение амплитуды результирующей волны в разных его точках. Это явление называется интерференцией волн. Контрольное задание №1 Вариант 1 1. Тело движется по прямой согласно уравнению S = 0,5t4 + 0,2t2 +2. Найти скорость и ускорение тела в момент времени 4с. Каковы средние значения скорости и ускорения за первые 4 с движения? 2. Определить время полета самолета между двумя пунктами, находящимися на расстоянии 477 км, если скорость самолета относительно воздуха равна 280 м/с, а скорость встречного ветра, направленного под углом 140 к направлению движения, равна 16 м/с. 3. Тело вращается вокруг неподвижной оси по закону: j =A+Вt+Сt2, где А=10рад, В = 20 рад/с, С =-2 рад/c2. Найти угловую скорость и угловое ускорение для момента времени t=5с. 4. Диск радиусом 2 м вращается согласно уравнению: j=А+Bt+Ct3, где
А=3 рад, В=-10 рад/с, С=0,1 рад/с3. Определить тангенциальное и нормальное ускорения точек на окружности диска для момента вращения t=10 с. 5. Два небольших тела массой 2 кг и 1 кг связаны невесомой и нерастяжимой нитью и расположены на горизонтальной плоскости. К первому телу приложена сила 10 Н, направленная под углом 300 к горизонту (вверх). Определить ускорение системы, если коэффициент трения тел о плоскость одинаков и равен 0,1. 6. Через блок перекинута нить, на концах которой висят два груза с одинаковыми массами М. Одновременно на каждый из грузов кладут по перегрузку: справа – массой 3m; слева массой – m. Определить ускорение системы, силу натяжения нити и силу давления перегрузков на основные грузы. 7. Камень брошен под углом к горизонту a = 60°. Кинетическая энергия ЕК0 камня в начальный момент времени равна 20 Дж. Определить кинетическую ЕК и потенциальную ЕП энергии камня в высшей точке его траектории. Сопротивлением воздуха пренебречь. 8. Наклонная плоскость имеет длину L = 5 м и высоту H = 3 м. Тело массой m = 400 кг прижимается к наклонной плоскости силой, параллельной ее основанию. Какой должна быть эта сила, чтобы тело двигалось равномерно вверх? Коэффициент трения о плоскость m = 0,1.
9. Падающий вертикально шарик массой 0,2 кг ударился об пол и подпрыгнул на высоту 0,4 м. Найти среднюю силу, действующую со стороны пола на шарик, если длительность удара 0,01 с. К моменту удара об пол скорость шарика равна 5 м/с. 10. Колесо, вращаясь при торможении равнозамедленно, уменьшило в течение времени t=1мин частоту своего вращения с 300 об/мин до 180 об/мин. Момент инерции колеса 2 кг×м2. Определить угловое ускорение колеса и тормозящий момент. 11. На полый тонкостенный цилиндр намотана нить, свободный конец которой прикреплен к потолку. Цилиндр сматывается с нити под действием собственного веса. Найти ускорение цилиндра и силу натяжения нити, если массой и толщиною нити можно пренебречь. Начальная длина нити намного больше радиуса цилиндра. 12. Круглая платформа радиусом 1 м, момент инерции которой 130 кг×м2, вращается по инерции вокруг вертикальной оси, делая 1 оборот в секунду. На краю платформы стоит человек, масса которого 60 кг. Сколько оборотов в секунду будет совершать платформа, если человек перейдет в ее центр? Момент инерции человека рассчитывать как для материальной точки. 13. Написать уравнение гармонических колебаний, совершающихся по закону косинуса. За время 1 мин совершается 60 колебаний, амплитуда которых 8 см, а начальная фаза равна 3/2π рад. Построить график зависимости смещения от времени. 14. Тонкий обруч радиусом 50 см подвешен на вбитый в стену гвоздь и колеблется в плоскости, параллельной стене. Найти период колебаний обруча. 15. Точка участвует в двух взаимно перпендикулярных колебаниях, выраженных уравнениями x=2cosωt и у=3sin0,5wt. Найти уравнение траектории точки и построить ее на чертеже.
Вариант 2 1. Уравнение движения материальной точки вдоль оси имеет вид x=A+Bt+Ct2, где A=2 м; B=1 м/с; C=-0,5 м/с2. Найти координату скорости и ускорения точки в момент времени t=2 с. 2. Тело брошено под углом к горизонту. Оказалось, что максимальная высота подъема равна дальность полета. Пренебрегая сопротивлением воздуха, определить угол броска к горизонту. 3. Колесо при вращении имеет начальную частоту 5 с-1, после торможения его частота уменьшилась до 3 с-1. Найти угловое ускорение колеса и число оборотов, сделанных им за это время. 4. Диск радиусом r = 20 см вращается согласно уравнению j = A + Bt + Ct3, где A = 3 рад; B = – 1 рад/с; C = 0,1 рад/с3. Определить at тангенциальное, an нормальное и полное a ускорения точек на окружности диска для момента времени, равного t = 10 с. 5. Две гири массой 1 кг и 2 кг соединены невесомой нерастяжимой нитью, перекинутою через невесомый блок, подвешенный к динамометру. Какое значение покажет динамометр во время движения грузов? Трения в оси блока нет. 6. Определить работу, совершаемую при подъеме груза массой m =50 кг по наклонной плоскости с углом наклона a = 30° к горизонту на высоту h = 4 м, если время подъема t = 2 с, а коэффициент трения m = 0,06. 7. Материальная точка массой 1 кг движется под действием силы согласно уравнению х=10-2t2-0,2t3 (длина в метрах, время в секундах). Найти мощность, затрачиваемую на движение точки в момент времени равной 3 секундам. 8. Тело массой 990 г лежит на горизонтальной поверхности. В него попадает пуля массой 10 г и застревает в нем. Скорость пули равна 700 м/с и направлена горизонтально. Какой путь пройдет тело до остановки? Коэффициент трения между телом и поверхностью равен 0,05. 9. Камень массой 0,5 кг бросили под углом к горизонту с некоторой начальной скоростью. Его начальная кинетическая энергия равна 25 Дж. На высоте 2 м скорость камня равна v. Определить начальную скорость камня, скорость камня на высоте 2 м и угол, под которым бросили камень. 10. Найти момент инерции тонкого стержня длиной 50 см и массой 0,36 кг относительно оси, перпендикулярной стержню и проходящей через: 1) конец стержня; 2) точку, отстоящую от стержня на 1/6 его длины. 11. Маховик в виде сплошного диска, момент инерции которого равен 150 кг×м2, вращается с частотой 240 об/мин. Через минуту он остановился. Определить момент сил торможения, угловое ускорение, число оборотов маховика со времени начала торможения до полной остановки. 12. Полый тонкостенный цилиндр массой 500 г, катящийся без скольжения, ударяется о стенку и отскакивает от нее. Скорость цилиндра до удара о стенку равна 1,4 м/с, после удара 1 м/с. Определить выделившееся при ударе количество теплоты. 13. Уравнение движения материальной точки задано в виде x=2sin(π/2t +π/4) м. Определить период колебаний точки и максимальные значения ее скорости и ускорения. 14. Математический маятник, отведенный на натянутой нити на угол α от вертикали, проходит положение равновесия со скоростью v. Считая колебания гармоническими, найти частоту ω0 собственных колебаний маятника. 15. Точка участвует одновременно в двух колебаниях одного направления, происходящих согласно уравнениям x1=2sinωt и x2=2sin(ωt+π/2). Записать уравнение результирующего колебания и представить векторную диаграмму сложения амплитуд. Определить скорость и ускорение результирующего колебания. Вариант 3 1. Движение двух материальных точек выражаются следующими уравнениями: x1=A1+B1t+C1t2, x2=A2+B2t+C2t2 , где A1=20 м; A2 =2 м; B2=B1=2 м/с; C1=-4м/с; C2=0,5 м/c2. В какой момент времени скорости этих точек будут одинаковыми? Определить скорости и ускорения точек в этот момент. 2. Камень падает с высоты h = 1200 м. Какой путь пройдет камень за последнюю секунду своего падения? 3. Тело брошено с начальной скоростью 20 м/с под углом 600 к горизонту. Найти радиус кривизны траектории в точке наивысшего подъема тела над поверхностью земли. 4. Диск радиусом 20 см вращается с угловым ускорением 3,14 рад/с2. Найти для точек, находящихся на краю диска, к концу второй секунды после начала движения: а) угловую скорость; б) линейную скорость; в) тангенциальное, нормальное и полное ускорения. 5. На наклонной плоскости укреплен блок, через который перекинута нить. К одному концу нити привязан груз массой 1 кг, лежащий на наклонной плоскости. На другом конце нити висит груз массой 3 кг. Наклонная плоскость образует с горизонтом угол в 300. Коэффициент трения между грузом и наклонной плоскостью равен 0,1. Определить ускорение грузов. 6. Брусок скользящий по гладкой горизонтальной поверхности, со скоростью 5 м/с наезжает на шероховатую поверхность с коэффициентом трения, равным 0,8. При какой длине бруска его задняя грань остановится на границе гладкой и шероховатой поверхностей? 7. Какую работу совершает двигатель автомобиля массой m = 1,3 т при движении с места на первых S = 75 м пути, если это расстояние автомобиль проходит за t = 10 с, а коэффициент сопротивления движению равен m = 0,05? 8. Молекула летит со скоростью 500 м/с и упруго ударяется о поршень, движущийся навстречу ей. Скорость молекулы составляет угол в 600 с нормалью поршня. Определить величину и направление скорости молекулы после удара. Скорость поршня равна 20 м/с. 9. К ободу колеса, имеющему форму диска, радиус которого равен 0,5 м, а масса 50 кг, приложена касательная сила, равная 100 Н. Найти: а) угловое ускорение колеса; б) через какое время после начала действия силы колесо будет иметь частоту вращения 100 об/с. 10. На краю горизонтальной платформы, имеющей форму диска радиусом 2 м и массой 4 кг, стоит человек, масса которого равна 80 кг. Платформа может свободно вращаться вокруг вертикальной оси, проходящей через ее центр. С какой угловой скоростью будет вращаться платформа, если человек идет вдоль ее края со скоростью 2 м/с относительно платформы? 11. Определить момент инерции однородного диска радиусом 20 см и массой 1 кг относительно оси, перпендикулярной плоскости диска и проходящей через: а) центр диска; б) середину одного из радиусов диска. 12. Кинетическая энергия вала, вращающегося с постоянной частотой 6 об/с, равна 60 Дж. Найти момент импульса этого вала. 13. Материальная точка совершает гармонические колебания с частотой 0,5 Гц. Амплитуда колебания равна 3 см. Определить скорость точки в момент времени, когда смещение равно 1,5 см. 14. Как относятся длины математических маятников, если за одно и то же время один совершил 10, а другой 30 колебаний? 15. Вынужденные колебания описываются дифференциальным уравнениeм 0,1
Вариант 4 1. Кинематические уравнения движения двух материальных точек имеют вид x1 = A1t + B1t2 + C1t3 и x2 = A2t + В2t2 + С2t3, где В1 = 4 м/с2,
|
||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 212; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.244.136 (0.014 с.) |

 ,
,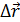 - перемещение;
- перемещение; 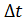 - время движения.
- время движения. ,
, - время движения.
- время движения. ,
, – радиус-вектор.
– радиус-вектор. , где
, где  - проекции вектора скорости
- проекции вектора скорости  на оси координат. Если известна зависимость пути
на оси координат. Если известна зависимость пути  , пройденного материальной точкой, от времени ее движения
, пройденного материальной точкой, от времени ее движения  , то модуль мгновенной скорости:
, то модуль мгновенной скорости:  .
.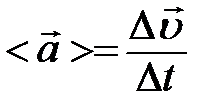 , где
, где  - изменение вектора скорости
- изменение вектора скорости 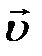 за время ∆
за время ∆  .
. .
. ) вдоль оси
) вдоль оси  :
: .
. .
.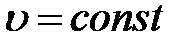 и координата материальной точки:
и координата материальной точки: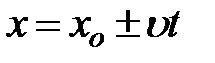 .
.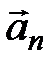 и тангенциальной
и тангенциальной 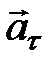 составляющих:
составляющих:  , где
, где  , (R – радиус вписанной окружности);
, (R – радиус вписанной окружности);  .
.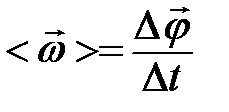 , где
, где 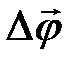 - изменение угла поворота точки за время ∆
- изменение угла поворота точки за время ∆ 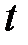 .
. .
. ,
, - изменение угловой скорости материальной точки за время ∆ t.
- изменение угловой скорости материальной точки за время ∆ t.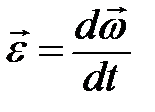 .
. , где
, где 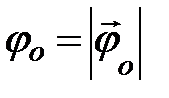 - модуль начального угла и
- модуль начального угла и  - модуль вектора угловой скорости. При равномерном вращении
- модуль вектора угловой скорости. При равномерном вращении  и
и  . Частота вращения равна
. Частота вращения равна  или
или  , где N - количество оборотов материальной точки за время
, где N - количество оборотов материальной точки за время  ; T - период вращения.
; T - период вращения. ) материальной точки:
) материальной точки:  .
. .
. ;
;  ;
; 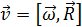 ;
;  ;
;  ;
;  .
. ,
, - импульс материальной точки массой
- импульс материальной точки массой  ,
,  - результирующая сила.
- результирующая сила.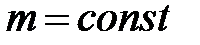 :
:  .
. .
. , где k – коэффициент упругости и x – изменение длины тела.
, где k – коэффициент упругости и x – изменение длины тела. ,
, - гравитационная постоянная,
- гравитационная постоянная,  и
и  - массы тел;
- массы тел;  - расстояние между центрами масс тел.
- расстояние между центрами масс тел. , где μ – коэффициент трения и
, где μ – коэффициент трения и  – нормальная составляющая реакции опоры.
– нормальная составляющая реакции опоры. или
или 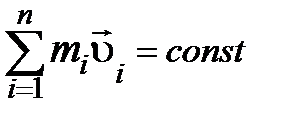 .
. :
:  FΔr cos α,
FΔr cos α, - перемещение тела, α – угол между векторами силы и перемещения.
- перемещение тела, α – угол между векторами силы и перемещения.
 :
: 
 , или
, или  =
= 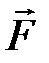
 = F
= F  cos α,
cos α, и скорости
и скорости 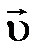 .
. или
или 
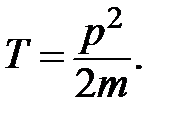
 ,
, .
. ,
, и
и 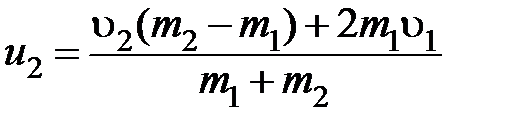 ,
, и
и  - проекции первоначальных скоростей шаров, имеющих, соответственно, массы
- проекции первоначальных скоростей шаров, имеющих, соответственно, массы  , действующей на тело, относительно точки O:
, действующей на тело, относительно точки O:  ,
, - радиус-вектор, проведенный из точки О в точку приложения силы
- радиус-вектор, проведенный из точки О в точку приложения силы  ,
, - угол между векторами
- угол между векторами 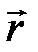 ,
,  - плечо силы.
- плечо силы. ,
,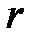 - расстояние этой точки до оси.
- расстояние этой точки до оси. ,
, – масса
– масса  –го элемента объема тела,
–го элемента объема тела,  - расстояние
- расстояние 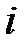 –го элемента объема до оси.
–го элемента объема до оси. .
. , где m – масса стержня и
, где m – масса стержня и  - его длина.
- его длина. .
. ,
, ,
, - его радиус.
- его радиус. ,
, - его радиус.
- его радиус. ,
, - момент инерции тела относительно параллельной оси, проходящей через центр масс тела; m – масса тела и
- момент инерции тела относительно параллельной оси, проходящей через центр масс тела; m – масса тела и  - расстояние между указанными осями.
- расстояние между указанными осями. ,
, - момент инерции тела относительно неподвижной оси;
- момент инерции тела относительно неподвижной оси;  - угловая скорость тела.
- угловая скорость тела. ,
, - момент силы
- момент силы  , действующей на тело, относительно точки O, находящейся на неподвижной оси.
, действующей на тело, относительно точки O, находящейся на неподвижной оси. ,
, - момент инерции тела относительно неподвижной оси;
- момент инерции тела относительно неподвижной оси;  - угловое ускорение тела.
- угловое ускорение тела. ,
, и
и  ,соответственно, начальный и конечный моменты инерций системы тел;
,соответственно, начальный и конечный моменты инерций системы тел; 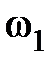 и
и  , соответственно, начальная и конечная угловые скорости этой системы тел.
, соответственно, начальная и конечная угловые скорости этой системы тел. ,
, ,
,  и
и  ,
, 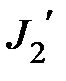 ,соответственно, начальные и конечные моменты инерций тел;
,соответственно, начальные и конечные моменты инерций тел; 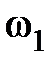 ,
,  и
и  ,
, 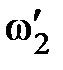 ,соответственно, начальные и конечные угловые скорости этих тел.
,соответственно, начальные и конечные угловые скорости этих тел. , действующего на вращающееся тело:
, действующего на вращающееся тело:  , где
, где 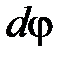 - угол поворота тела.
- угол поворота тела. , где
, где  - мгновенная угловая скорость тела.
- мгновенная угловая скорость тела.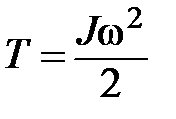 ,
, - момент инерции тела относительно его оси вращения.
- момент инерции тела относительно его оси вращения. ,
, - масса тела;
- масса тела; 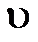 - скорость движения центра масс тела;
- скорость движения центра масс тела;  - момент инерции тела и
- момент инерции тела и  - угловая скорость вращения тела относительно оси, проходящей через центр масс этого тела.
- угловая скорость вращения тела относительно оси, проходящей через центр масс этого тела. .
.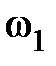 и
и  ,соответственно, начальная и конечная угловые скорости тела.
,соответственно, начальная и конечная угловые скорости тела.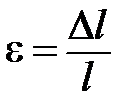 .
. - начальная длина тела,
- начальная длина тела,  - изменение его длины.
- изменение его длины. ,
, , где
, где  - модуль Юнга.
- модуль Юнга. ,
, - первоначальный объем тела.
- первоначальный объем тела. ,
,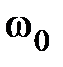 - циклическая (круговая) частота;
- циклическая (круговая) частота;  - начальная фаза колебаний в момент времени t = 0,
- начальная фаза колебаний в момент времени t = 0,  - фаза колебаний в момент времени t.
- фаза колебаний в момент времени t. ,
, - линейная частота колебаний;
- линейная частота колебаний;  - период колебаний.
- период колебаний. .
. .
. результирующего колебания, полученного при сложении двух гармонических колебаний с одинаковыми частотами, происходящих по одной прямой
результирующего колебания, полученного при сложении двух гармонических колебаний с одинаковыми частотами, происходящих по одной прямой и
и 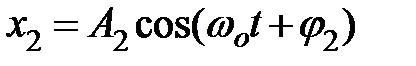 ,
,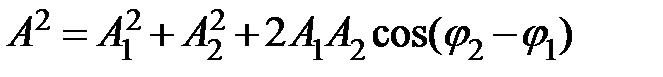 ,
, ,
,  и
и  ,
,  - амплитуды и начальные фазы складываемых колебаний.
- амплитуды и начальные фазы складываемых колебаний. результирующего гармонического колебания определяется по формуле:
результирующего гармонического колебания определяется по формуле:
 .
. .
.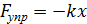 :
: или
или  ,
, - масса материальной точки;
- масса материальной точки;  - коэффициент упругости;
- коэффициент упругости;  - циклическая частота свободных незатухающих колебаний.
- циклическая частота свободных незатухающих колебаний. .
.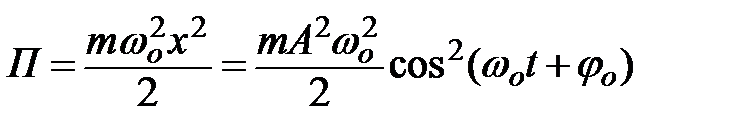 .
.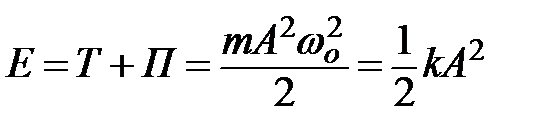 .
. ,
, - масса маятника,
- масса маятника,  - коэффициент упругости пружины.
- коэффициент упругости пружины. ,
, - длина маятника;
- длина маятника;  - ускорение свободного падения.
- ускорение свободного падения.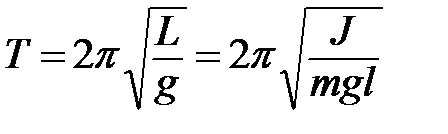 ,
,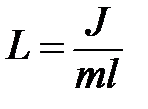 - приведенная длина физического маятника;
- приведенная длина физического маятника;  - момент инерции маятника относительно оси, проходящей через точку подвеса.
- момент инерции маятника относительно оси, проходящей через точку подвеса. или
или  ,
, - масса маятника;
- масса маятника;  - коэффициент упругости пружины;
- коэффициент упругости пружины;  - коэффициент сопротивления среды;
- коэффициент сопротивления среды;  - коэффициент затухания;
- коэффициент затухания;  - циклическая частота свободных незатухающих колебаний.
- циклическая частота свободных незатухающих колебаний. ,
, - амплитуда затухающих колебаний;
- амплитуда затухающих колебаний; 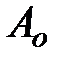 - амплитуда колебаний в момент времени
- амплитуда колебаний в момент времени  ;
; 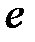 - основание натурального логарифма;
- основание натурального логарифма;  - коэффициент затухания;
- коэффициент затухания; 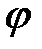 - начальная фаза затухающих колебаний.
- начальная фаза затухающих колебаний. .
. ,
,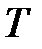 - период затухающих колебаний;
- период затухающих колебаний;  - время релаксации;
- время релаксации;  - число колебаний, совершаемых за время уменьшения амплитуды в
- число колебаний, совершаемых за время уменьшения амплитуды в  раз.
раз. или
или  ,
, – внешняя приведенная периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания,
– внешняя приведенная периодическая сила, действующая на колеблющуюся материальную точку и вызывающая вынужденные колебания, – её амплитудное значение,
– её амплитудное значение, 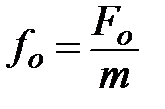 .
. .
. и
и  .
. ,
, - скорость распространения волны,
- скорость распространения волны,  - период колебаний физических величин в данной точке пространства.
- период колебаний физических величин в данной точке пространства. ,
, - линейная частота колебаний физических величин.
- линейная частота колебаний физических величин. :
:  ,
,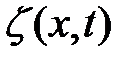 - колеблющаяся физическая величина;
- колеблющаяся физическая величина;  - амплитуда колеблющейся физической величины;
- амплитуда колеблющейся физической величины; 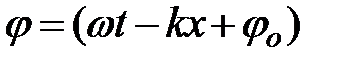 - фаза волны;
- фаза волны;  - циклическая частота;
- циклическая частота; 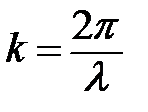 - волновое число;
- волновое число; 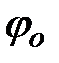 - начальная фаза волны.
- начальная фаза волны.

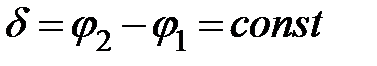 .
. и
и 
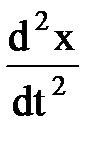 +0,12
+0,12  +0,4x = 0,4sin1,5t. При какой частоте внешней силы будет наблюдаться резонанс?
+0,4x = 0,4sin1,5t. При какой частоте внешней силы будет наблюдаться резонанс?


