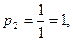Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра геодезии и геоинформатикиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
КАФЕДРА ГЕОДЕЗИИ И ГЕОИНФОРМАТИКИ
ГЕОДЕЗИЯ ЧАСТЬ III МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ Для студентов очного и заочного обучения по направлению: Землеустройство и кадастры»
Москва 2012 УДК 528
Одобрено и рекомендовано к изданию кафедрой геодезии и геоинформатики Государственного университета по землеустройству (протокол № 8 от 7 февраля 2012 г.). Утверждено к изданию методической комиссией факультета городского кадастра Государственного университета по землеустройству (протокол № 4 от 22. февраля 2012 г.).
Составители: ст. пр. Ктиторов Э.М., доц., к.т.н. Парамонова Е.Г., ст. пр., к.т.н. Симонян В.В., ст. пр. Журавлев А.Ф., ст. пр. Каширкин Ю.Ю.
Рецензент: доц., к.т.н. Лимонов А.Н.
Содержание методических указаний соответствует программе дисциплины «Геодезия» и помогает студентам выполнять контрольные работы.
Государственный университет по землеустройству, 2012 СОДЕРЖАНИЕ ВВЕДЕНИЕ…………………………………………………………………………..4 1. МЕТОДИКА САМОСТОЯТЕЛЬНОГО ИЗУЧЕНИЯ КУРСА……………….5 1.1. Рекомендуемая литература …………...……………………………………..5 1.2. Основные разделы программы курса………………………………………..5 1.3. Рекомендации по изучению и усвоению основных разделов курса………5 2. КОНТРОЛЬНАЯ РАБОТА 1. ТАХЕОМЕТРИЧЕСКАЯ СЪЕМКА………….7 2.1. Задание………………………………………………………………………...7 2.2. Вычислительная обработка тахеометрического хода……………………...7 2.3. Вычисление координат точек тахеометрического хода…………………..12 2.4. Вычисление высот точек тахеометрического хода……………………….12 2.5. Вычисление высот съемочных пикетов……………………………………13 2.6. Составление плана участка…………………………………………………14 Вопросы для самопроверки………………………………………………………..16 3. КОНТРОЛЬНАЯ РАБОТА 2. ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ..…………………………………………………………………..17 3.1. Рекомендации по обработке вычислений…………………………………17 3.2. Оценка точности результатов измерении по истинным погрешностям...17 3.3. Оценка точности функций измеренных величин…………………………20 3.4. Математическая обработка ряда результатов равноточных измерений...25 3.5. Веса измерений и их функций……………………………………………..27
3.6. Математическая обработка ряда результатов неравноточных измерений………………………………………….………………….…….30 3.7. Оценка точности измерений углов и превышений по невязкам в полигонах и ходах……………………………………………………...…...34 3.8. Оценка надежности определения среднеарифметического с использованием доверительных интервалов……………………..………37 3.9. Справочные сведения………………………………………………………38 3.9.1. Округление приближенных чисел…………………………………………38 3.9.2. Точность приближенных чисел…………………………………………....38 3.9.3. Погрешности измерений……………………………………………………38 Вопросы для самопроверки………………………………………………………..39 4. КОНТРОЛЬНАЯ РАБОТА 3. УРАВНИВАНИЕ СИСТЕМЫ ТЕОДОЛИТНЫХ ХОДОВ С ОДНОЙ УЗЛОВОЙ ТОЧКОЙ..………………41 4.1. Общая постановка задачи…………………………………………………..41 4.2. Исходные данные…………………………………………………………...41 4.3. Последовательность выполнения работы…………………………………42 Вопросы для самопроверки………………………………………………………..47 ПРИЛОЖЕНИЕ…………………………………………………………………….48
ВВЕДЕНИЕ
Методические указания и задания для контрольных работ по курсу “Геодезия” предназначены для студентов очной и заочной форм обучения по направлению: 120700 – «Землеустройство и кадастры». Студенты-заочники, пользуясь данными методическими указаниями, должны самостоятельно изучить предусмотренные программой разделы курса “Геодезия” по рекомендуемой учебной и справочной литературе и выполнить следующие контрольные работы: 1. Тахеометрическая съемка. 2. Теория погрешностей измерений. 3. Уравнивание системы теодолитных ходов с одной узловой точкой. Предварительно проверенные преподавателем контрольные работы представляются для защиты и получения допуска к экзамену в период лабораторно-экзаменационной сессии. На очной сессии студенты прослушивают курс лекций, а также выполняют лабораторные работы по темам: измерение углов и линий в геодезических сетях сгущения; решению задач по теории погрешностей, определению координат отдельных пунктов; расчетам координат рамок трапеций топографических карт.
Изучение основных вопросов курса рекомендуется в последовательности, предлагаемой в программе. Контрольные работы следует выполнять после усвоения соответствующих разделов теории. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ САМОСТОЯТЕЛЬНОГО ИЗУЧЕНИЯ КУРСА РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Основная 1. Маслов А.В., Гордеев А.В., Батраков Ю. Г. Геодезия. – М., КолосС, 2006. 2. Неумывакин Ю.К.,Практикум по геодезии. – М.; КолосС, 2008. 3. А.Г. Юнусов, А.Б. Беликов, В.Н. Баранов, Ю.Ю. Каширкин, Геодезия. – М. академический Проект, 2011 г. Дополнительная 4. Батраков Ю.Г. Геодезические сети специального назначения. М.; Картгеоцентр – Геодезиздат, 1999. 5. Инструкция по развитию съемочного обоснования и съемке ситуации и рельефа с применением глобальных навигационных спутниковых систем ГЛОНАСС и GPS. – М.: ЦНИИГАиК, 2002. 6. Инструкция по топографической съемке в масштабах 1:5000, 1:2000, 1:1000 и 1:500. – М.; ФГУП "Картгеоцентр", 2004. 7. Основные положения о государственной геодезической сети Российской Федерации. – М., 2004 г. 8. Таблицы координат Гаусса-Крюгера и таблицы размеров рамок и площадей трапеций топографических съемок. – М.; Недра, 1963. 9. Условные знаки для топографических планов масштабов 1:500 – 1:5000. – М.; Недра, 1989.
ОСНОВНЫЕ РАЗДЕЛЫ ПРОГРАММЫ КУРСА
Раздел 1. Тахеометрическая съемка. Раздел 2. Теория погрешностей измерений. Раздел 3. Общие сведения о построении геодезической сети при съемке на большой территории. Раздел 4. Плоские прямоугольные координаты Гаусса-Крюгера. Номенклатура листов топографических карт. Раздел 5. Методы измерения и приборы, применяемые при создании геодезических сетей сгущения. Раздел 6. Методы определения положения отдельных пунктов. Раздел 7. Уравнивание геодезических сетей сгущения.
РЕКОМЕНДАЦИИ ПО ИЗУЧЕНИЮ И УСВОЕНИЮ ОСНОВНЫХ РАЗДЕЛОВ КУРСА
Раздел 1. Перед выполнением контрольной работы 1 – «Тахеометрическая съемка» необходимо изучить 8.1 – 8.5 учебника [1]. Особое внимание должно быть уделено методике проложения и обработки тахеометрических ходов выполненной тахеометрической съемки, и составлению плана по результатам тахеометрической съемки. Исходные данные для выполнения контрольной работы выбираются в табл. 1 (см. приложение). Номер варианта задания равен двум последнимцифрамномера зачетной книжки. Если две последние цифры номера зачетной книжки обозначают число большее пятидесяти, то номер варианта равен двум последним цифрам минус 50. Номер варианта не может превышать 50. Например, если номер зачетной книжки 20023, то номер варианта равен 23. Если номер зачетной книжки 20065, то номер варианта 65-50=15. Прочитать 8.7 – 8.10 учебника [1] и 11.4.2. [2] чтобы иметь представление об электронных тахеометрах и особенностях выполнения тахеометрической съемки электронными тахеометрами. Раздел 2. Перед выполнением контрольной работы 2 – «Теория погрешностей измерений»необходимо изучить его по учебнику [1] 9.1 – 9.23. Следует обратить внимание на определения и формулы вычисления: погрешности, дисперсии, среднеквадратических погрешностей (СКП), предельной погрешности, веса, СКП погрешности единицы веса, среднеарифметического и средневесового. Студент при этом должен четко представлять разницу между равноточными и неравноточными измерениями, знать правила их обработки и оценки точности, уметь использовать общую формулу для оценки точности функций измеренных величин, а также формулы для оценки точности по невязкам в полигонах и ходах.
После изучения теоретических вопросов необходимо освоить решение типовых задач раздела 2 данных методических указаний. Только после этого следует приступать к решению контрольных задач, руководствуясь рекомендациями раздела 2. Разделы 3, 4, 5, 6 изучаются по учебнику [1] (главы 10, 11, 12, 13, 15), [3], [4], [6], [7]. Студент должен разобраться со схемами и методами создания геодезических сетей, сетей сгущения и съемочных сетей. При изучении плоских прямоугольных координат Гаусса-Крюгера необходимо обратить особое внимание на вопросы искажения изображений длин линий и площадей, а также разобраться с номенклатурой топографических карт и планов. Лабораторные работы по этим разделам курса студент выполняет в период сессии. При этом непосредственно перед проведением лабораторных работ по вычислению координат отдельных пунктов необходимо ознакомиться с разделом 6 настоящих методических указаний. Раздел 7. Перед выполнением контрольной работы 3 – «Уравнивание системы теодолитных ходов с одной узловой точкой» необходимо по учебнику [1] изучить 18.1, 18.2. КОНТРОЛЬНАЯ РАБОТА 1 «ТАХЕОМЕТРИЧЕСКАЯ СЪЕМКА» ЗАДАНИЕ По полевым материалам: журналу тахеометрической съемки и абрисам произвести необходимые вычисления и составить топографический план участка в масштабе 1: 2000 с высотой сечения рельефа горизонталями через 1 м. Измерения выполнялись теодолитом 4Т30П. Исходные данные: – координаты и высоты исходных точек и дирекционные углы начальной и конечной сторон хода выбираются по варианту индивидуального задания (см. Приложение, табл.1); – журнал с результатами полевых измерений – табл. 2.1.; – абрис (рис. 2.1., 2.2.).
Таблица 2.1. Таблица 2.2. Ведомость вычисления высот точек тахеометрического хода
СОСТАВЛЕНИЕ ПЛАНА УЧАСТКА
На чертежной бумаге размером 35
По координатам нанести все точки тахеометрического хода. Возле каждой точки записать в виде дроби: в числителе номер точки, а в знаменателе (взятую из табл. 2.2) ее высоту с точностью до сотых долей метра. Используя геодезический транспортир и поперечный масштаб, нанести на план пикетные точки и справа записать их высоты, округленные до десятых долей метра. По данным абриса нанести на план границы угодий, ручей, озеро. По высотам пикетных точек выполнить интерполяцию горизонталей по направлениям, указанным на абрисах стрелками и провести горизонтали через 1 м по высоте. Следует иметь в виду, что интерполяцию можно производить только между пикетами, соединенными стрелками, в т.ч. и по ручью. Если между двумя пикетами проходят несколько горизонталей, то они должны находиться на одинаковом расстоянии друг от друга. Урез воды в озере подписать как среднее арифметическое из всех значений высот уреза с округлениями до 0,1 м. Все элементы ситуации и рельеф вычертить тушью, оформляя план в соответствии с условными знаками [8]. При этом необходимо тщательно выдерживать очертания, размеры и порядок размещения условных знаков. Горизонтали вычертить и подписать коричневой тушью толщиной 0,15 мм. Высоты точек съемочного обоснования и пикетов подписать черной тушью. Линию уреза воды в озере и ручей провести синей тушью. Рамку плана и все остальные условные знаки и надписи выполнить черной тушью. Над северной стороной рамки подписать название, под южной стороной рамки указать численный масштаб плана, высоту сечения рельефа и сведения о съемке. Тип и размер шрифтов при оформлении плана должен соответствовать условным знакам для масштаба 1:2 000 Пример оформления рамки тахеометрической съемки масштаба 1:2000 приведен на рис.2.3.
Вопросы для самопроверки
1. Какова цель тахеометрической съемки? 2. Как определяют при тахеометрической съемке плановое положение съемочных пикетов и их высоты? 3. В чем различие между абрисами тахеометрической и теодолитной съемок? 4. Для чего выполняют ориентировку лимба на станции? 5. По какой формуле вычисляют допустимое расхождение между прямыми и обратными горизонтальными проложениями, измеренными по нитяному дальномеру? 6. Какое допустимое расхождение между значениями прямых и обратных превышений? 7. По какой формуле вычисляют допустимую абсолютную невязку тахеометрического хода? 8. По какой формуле вычисляют допустимую невязку в сумме превышений тахеометрического хода? 9. По какой формуле вычисляют высоты пикетов? 10. По какой формуле вычисляют горизонтальные проложения, если углы наклона 11. Как производят интерполирование высот на плане для проведения горизонталей?
КОНТРОЛЬНАЯ РАБОТА 2 «ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ» РЕКОМЕНДАЦИИ ПО ОБРАБОТКЕ ВЫЧИСЛЕНИЙ Для выполнения контрольной работы по теме «Теория погрешностей измерений» необходимо решить около тридцати контрольных задач. Контрольная работа выполняется в соответствии с вариантами, указанными в табл. 2 (см. Приложение). Номер варианта определяется так же, как и в контрольной работе 1 (последние 2 цифры номера зачётной книжки минус 30).
Для подготовки работы к защите необходимо изучить теоретический материал, относящийся к перечню вопросов, приведенных в конце раздела. При решении контрольных задач необходимо обратить внимание на следующее: 1. При вычислении СКП и весов результатов измерений в промежуточных вычислениях следует удерживать две-три значащие цифры. Причем, в случае суммирования в наибольшем по абсолютной величине слагаемом оставлять две значащие цифры, остальные слагаемые вычислять с тем же числом десятичных знаков, которое будет иметь наибольшее слагаемое. Окончательные значения следует округлять до двух значащих цифр. 2. Вычисления по формулам следует приводить к виду:
или
где [ ] – символ суммы, введенный К.Ф.Гауссом.
ИСТИННЫМ ПОГРЕШНОСТЯМ
Для оценки точности результатов измерений применяют формулу Гаусса
где n – число измерений. Истинная погрешность результата измерения
где l –результат измерения; a – истинное значение измеряемой величины. Оценка точности определения самой погрешности m (СКП самого СКП)
Предельную погрешность измерения
где
Решение задач Пример 1. Линия теодолитного хода измерена мерной лентой пять раз. При этом получены результаты: 217,24; 217,31; 217,28; 217,23; 217,20 м. Эта же линия измерена светодальномером, что дало результат 217,236 м. Найти СКП измерения линии мерной лентой, если результат измерения линии светодальномером принят за точное (истинное) значение длины линии. Решение. Результаты расчетов сведены в таблицу 3.1 (табличная форма). Табл. 3.1
СКП равна
СКП самой СКП
Следовательно,
Предельная погрешность равна
Погрешности всех пяти измерений меньше предельной погрешности, следовательно, нет оснований предполагать, что измерения имеют грубые погрешности. Пример 2. Площадь теодолитного полигона была измерена 8 раз планиметром (см. табл. 3.2). Та же площадь была вычислена аналитическим методом и получен результат 124,32га. Приняв этот результат за точное значение площади полигона a, вычислить СКП и предельную погрешности измерения площади планиметром. Решение. Табл. 3.2
Задача 1. Для исследования точности измерения горизонтального угла полным приемом теодолитом 3Т5КП, им был многократно измерен угол. Результаты оказались следующими: 39°17,4′; 39º 16,8′; 39°16,6′; З9º16,2′; 39°15,5′; 39°15,8′; 39°16,3′; 39°16,2′. Тот же угол был измерен высокоточным теодолитом 3Т2КП, что дало результат (см. приложение табл. 2). Приняв это значение за точное, вычислить: - СКП измерений угла; - определить СКП самого СКП; - найти предельную погрешность. Задача 2. Дана совокупность угловых невязок в треугольниках объемом 50 единиц. На данной совокупности проверить свойства случайных погрешностей. Считая невязки истинными погрешностями, вычислить СКП и произвести оценку точности СКП, вычислить предельную погрешность.
Решение задач Пример 3. Пусть проложен висячий теодолитный ход. Горизонтальные углы хода Решение. Для определения погрешности дирекционного угла последней линии,прежде всего, необходимо представить этот дирекционный угол как функцию исходных и измеренных величин. Так как были измерены правые по ходу углы, искомый дирекционный угол может быть вычислен по формуле
На основании формулы (3.6) для СКП дирекционного угла последней линии хода можно записать
Получим
или
Окончательно можно сделать вывод, что при передаче дирекционных углов случайные погрешности накапливаются пропорционально корню квадратному из числа измеренных горизонтальных углов. Пример 4. Для получения горизонтального проложения линии на плане определены координаты концов этой линии, что дало результаты Решение Горизонтальное проложение между точками определяют по формуле:
Применим формулу (3.6) и вычислим частные производные
Аналогично:
Тогда СКП горизонтального проложения определяется формулой
При условии, что
или
Пример 5. Для получения дирекционного угла направления между точками на плане определены координаты концов отрезка, соединяющие эти точки ( Решение. Дирекционный угол направления вычисляют по формуле:
где Согласно (3.6) необходимо вычислить частные производные
Окончательно:
Аналогично найдем частные производные
СКП дирекционного угла определяется формулой
где При условии, что
Пример 6. Вычислить приращения координат и их СКП по линии длиной 250,17 м, имеющей дирекционный угол 63°27,0', если Решение. Известно, что приращения координат
Найдем
Тогда
При вычислениях величина
Подставив соответствующие значения величин, получаем
Окончательно
Задача 3. Найти СКП превышения, полученного из геометрического нивелирования методом из середины по черным сторонам реек, принимая СКП отсчета по рейке Задача 4. Линия теодолитного хода Задача 5. Определить СКП превышения, вычисленного на станции геометрического нивелирования методом из середины по черным и красным сторонам реек, если СКП отсчета по рейке Задача 6. Вычислить превышение, полученное тригонометрическим нивелированием, и его предельную погрешность, если расстояние, измеренное нитяным дальномером D =210,5 м с СКП Задача 7. При определении расстояния АВ, недоступного для измерения лентой, в треугольнике AВС были измерены: базис AС =84,55 м с СКП базиса Вычислить расстояние АВ и ее СКП. Задача 9. В треугольнике измерены основание Задача 10. В треугольнике измерены две стороны
РАВНОТОЧНЫХ ИЗМЕРЕНИЙ
При математической обработке ряда равноточных измерений одной и той же величины вычисляют: 1) среднеарифметическое значение измеренной величины (как наиболее надежное)
где
2) СКП одного измерения по формуле Бесселя:
где 3) СКП среднеарифметического
4) СКП самой СКП
Решение задач Пример 7. Линия теодолитного хода измерена мерной лентой пять раз. Получены следующие результаты: 217,24 м; 217,31 м; 217,38 м; 217,23 м; 217,20 м. Произвести математическую обработку ряда равноточных измерений. Решение.
217,272 Контроль:
За счет округления величины В этом случае контролем вычисления [ Контроль вычисления
СКП одного измерения будет равна
Оценка точности СКП
Следовательно,
СКП среднеарифметического значения равна
Ответ: Задача 13. Горизонтальный угол измерен 5 раз. Получены результаты: 60°41,0'; 60º40,5'; 60°40,0'; 60°42,0';.... (см. приложение табл. 2). Произвести обработку этого ряда результатов измерений. Задача 14. Площадь контура измерена планиметром 5 раз. Получены результаты: 26,31; 26,28; 26,32; 26,26;.… га (см. приложение табл. 2).Произвести обработку этого ряда результатов измерений. Задача 15. Линия теодолитного хода измерена мерной лентой пять раз. При этом получены результаты: 175,24; 175,31; 1175,28; 175,23;.... м (см. приложение табл. 2). Произвести математическую обработку результатов этого ряда измерений.
Решение задач Пример 8. Измерены два угла с СКП, соответственно равными Решение. Веса заданных величин будут
а в качестве величины, обладающей единичным весом, выступает угол, точность измерения которого характеризуется СКП равной 1². Пример 9. Вычислить вес
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 623; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.185.207 (0.013 с.) |

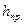 =
Σ
=
Σ  =
=
 =
=
 =
=
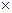 45 см построить координатную сетку со сторонами 10 см. Значение подписей координат линий сетки для масштаба 1: 2000 должны быть кратны 0,2 км.
45 см построить координатную сетку со сторонами 10 см. Значение подписей координат линий сетки для масштаба 1: 2000 должны быть кратны 0,2 км.
 >|3°|?
>|3°|? ,
,  ,
, ,
, , (3.1)
, (3.1)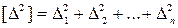 – сумма квадратов погрешностей измерений;
– сумма квадратов погрешностей измерений; вычисляется по формуле:
вычисляется по формуле: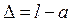 , (3.2)
, (3.2) , (3.3)
, (3.3) вычисляют по формуле
вычисляют по формуле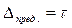
 , (3.4)
, (3.4) – коэффициент, принимающий значения в соответствии с выбранной доверительной вероятностью. Для вероятности Р = 0,997 коэффициент
– коэффициент, принимающий значения в соответствии с выбранной доверительной вероятностью. Для вероятности Р = 0,997 коэффициент 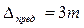 .
. м
м

 =87,8
=87,8 см.
см.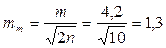 см.
см.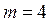 см.
см. .
. , га
, га

 ;
; ;
; ;
; .
.
 измерялись независимо друг от друга в одинаковых условиях с СКП
измерялись независимо друг от друга в одинаковых условиях с СКП  . Найти СКП
. Найти СКП  дирекционного угла последней линии рассматриваемого хода. При этом будем считать
дирекционного угла последней линии рассматриваемого хода. При этом будем считать  величиной безошибочной.
величиной безошибочной.
 .
. ,
,
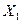 ,
,  и
и  ,
,  . Эти величины получены со СКП
. Эти величины получены со СКП  и
и  ,
,  и
и 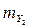 . Необходимо вычислить горизонтальное проложение между этими точками и его СКП.
. Необходимо вычислить горизонтальное проложение между этими точками и его СКП.
 по всем координатам:
по всем координатам: .
.

 .
.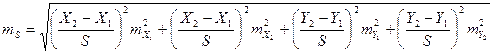 .
. , будем иметь:
, будем иметь: ,
,
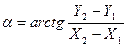 ,
, по всем координатам:
по всем координатам: .
.
 .
. 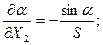
 .
.
 .
.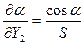 .
. ,
, - радианная мера угла в секундах, равная 206265".
- радианная мера угла в секундах, равная 206265". , будем иметь:
, будем иметь: .
. и
и 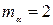 ,0'.
,0'.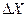 ,
, 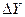 рассчитывают по формулам
рассчитывают по формулам  и
и  , что дает результаты
, что дает результаты  и
и  . СКП приращений координат могут быть получены из соотношений
. СКП приращений координат могут быть получены из соотношений ,
, .
. :
:
 ;
;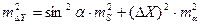 .
.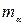 должна быть представлена в радианной мере, но в условии задачи она задается в градусной мере. С учетом этого предыдущие формулы примут вид
должна быть представлена в радианной мере, но в условии задачи она задается в градусной мере. С учетом этого предыдущие формулы примут вид ;
; .
.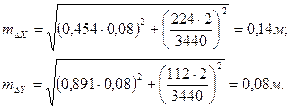


 равной 1 мм.
равной 1 мм. измерена частями с СКП
измерена частями с СКП  м,
м,  м,
м, 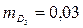 м. Определить СКП
м. Определить СКП  длины линии
длины линии  м; угол наклона визирной оси при визировании на верх рейки ν = ……(см. приложение табл. 2) с СКП
м; угол наклона визирной оси при визировании на верх рейки ν = ……(см. приложение табл. 2) с СКП  ; высота прибора i = 1,30 м с СКП
; высота прибора i = 1,30 м с СКП  м; длина рейки V = 3,00 м с СКП
м; длина рейки V = 3,00 м с СКП  м.
м. м; углы A=56°27,0' и С=35°14,0' со СКП, равной
м; углы A=56°27,0' и С=35°14,0' со СКП, равной  =0,5'.
=0,5'. и высота
и высота  с погрешностями, соответственно равными
с погрешностями, соответственно равными  и
и 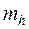 . Найти СКП площади треугольника.
. Найти СКП площади треугольника.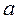 и
и 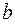 и угол
и угол 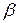 между ними с СКП, соответственно равными
между ними с СКП, соответственно равными  и
и  . Найти СКП площади треугольника.
. Найти СКП площади треугольника.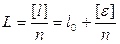 , (3.7)
, (3.7) – приближенное (как правило – наименьшее) значение измеряемой величины;
– приближенное (как правило – наименьшее) значение измеряемой величины; – остатки;
– остатки;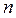 – число измерений;
– число измерений; , (3.8)
, (3.8) – поправки к результатам измерений (уклонения от средне-арифметического);
– поправки к результатам измерений (уклонения от средне-арифметического); . (3.10)
. (3.10)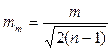 , (3.9)
, (3.9)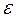 , см
, см



 =+36 [ V ]= -1
=+36 [ V ]= -1 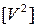 =211
=211  =470
=470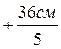

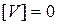 .
. .
. появляется ошибка округления
появляется ошибка округления  .
.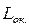 является выражение [
является выражение [  ]
]  .
. .
. 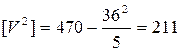 .
.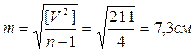 .
. .
. .
.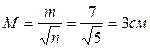 .
.
 0,03 м.
0,03 м.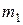 =5² и
=5² и  = 1². Вычислить веса этих результатов измерений, если
= 1². Вычислить веса этих результатов измерений, если 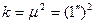 .
. ;
;