

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
контрольной работы 1 - «Тахеометрическая съемка»
| №
п/п
| 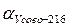 º ′
º ′
|  º ′
º ′
|  ,
м ,
м
|  ,
м ,
м
|  ,
м ,
м
|  ,
м ,
м
| |
| 221 11,0
| 353 41,0
| 4212,40
| - 2380,84
| 209,19
| 212,45
| |
| 221 16,5
| 353 46,5
| 4212,94
| - 2380,90
| 210,19
| 213,45
| |
| 221 21,0
| 353 51,0
| 4213,48
| - 2380,96
| 211,27
| 214,53
| |
| 221 26,5
| 353 56,5
| 4214,02
| - 2381,02
| 212,35
| 215,61
| |
| 221 31,0
| 354 01,0
| 4214,56
| - 2381,08
| 213,43
| 216,69
| |
| 221 36,5
| 354 06,5
| 4215,10
| - 2381,14
| 214,51
| 217,77
| |
| 221 41,0
| 354 11,0
| 4215,64
| - 2381,20
| 215,59
| 218,85
| |
| 221 46,5
| 354 16,5
| 4216,18
| - 2381,26
| 216,67
| 219,93
| |
| 221 51,0
| 354 21,0
| 4216,72
| - 2381,32
| 217,75
| 221,01
| |
| 221 56,5
| 354 26,5
| 4217,26
| - 2381,38
| 218,83
| 222,09
| |
| 222 01,0
| 354 31,0
| 4217,80
| - 2381,44
| 219,91
| 223,17
| |
| 222 06,5
| 354 36,5 4218,34
| - 2381,50
| 220,99
| 224,25
| |
| 222 11,0
| 354 41,0
| 4218,89
| - 2381,54
| 222,07
| 225,33
| |
| 222 16,5
| 354 46,5
| 4219,43
| - 2381,59
| 223,15
| 226,41
| |
| 222 21,0
| 354 51,0
| 4219,97
| - 2381,64
| 224,23
| 227,49
| |
| 222 26,5
| 354 56,5
| 4220,51
| - 2381,69
| 225,31
| 228,57
| |
| 222 31,0
| 355 01,0
| 4221,05
| - 2381,74
| 226,39
| 229,65
| |
| 222 36,5
| 355 06,5 4221,59
| - 2381,79
| 227,47
| 230,73
| |
| 222 41,0
| 355 11,0
| 4222,13
| - 2381,84
| 228,55
| 231,81
| |
| 222 46,5
| 355 16,5
| 4222,67
| - 2381,89
| 229,63
| 232,89
| |
| 222 51,0
| 355 21,0
| 4223,21
| - 2381,94
| 230,71
| 233,97
| |
| 222 56,5
| 355 26,5
| 4223,75
| - 2381,99
| 231,79
| 235,05
| |
| 223 01,0
| 355 31,0
| 4224,29
| - 2382,04
| 232,87
| 236,13
| |
| 223 06,5
| 355 36,5
| 4224,83
| - 2382,09
| 233,95
| 237,21
| |
| 223 11,0
| 355 41,0
| 4225,37
| - 2382,14
| 235,03
| 238,29
| |
| 223 16,5
| 355 46,5
| 4225,91
| - 2382,19
| 236,11
| 239,37
| |
| 223 21,0
| 355 51,0
| 4226,45
| - 2382,24
| 237,19
| 240,45
| |
| 223 26,5
| 355 56,5
| 4226,99
| - 2382,29
| 238,27
| 241,53
| |
| 223 31,0
| 356 01,0
| 4227,53
| - 2382,34
| 239,35
| 242,61
| |
| 223 36,5
| 356 06,5
| 4228,07
| - 2382,39
| 240,43
| 243,69
| |
| 223 41,0
| 356 11,0
| 4228,61
| - 2382,44
| 241,51
| 244,77
| |
| 223 46,5
| 356 16,5
| 4229,15
| - 2382,49
| 242,59
| 245,85
| |
| 223 51,0
| 356 21,0
| 4229,69
| - 2382,54
| 243,67
| 246,93
| |
| 223 56,5
| 356 26,5
| 4230,29
| - 2382,59
| 244,75
| 248,01
| |
| 224 01,0
| 356 31,0
| 4230,77
| - 2382,64
| 245,83
| 249,09
| |
| 224 06,5
| 356 36,5
| 4231,31
| - 2382,69
| 246,91
| 250,17
| |
| 224 11,0
| 356 41,0
| 4231,85
| - 2382,74
| 247,99
| 251,25
| |
| 224 16,5
| 356 46,5
| 4232,39
| - 2382,79
| 249,07
| 252,33
| |
| 224 21,0
| 356 51,0
| 4232,93
| - 2382,84
| 250,15
| 253,41
| |
| 224 26,5
| 356 56,5
| 4233,47
| - 2382,89
| 251,23
| 254,49
| |
| 224 31,0
| 357 01,0
| 4234,01
| - 2382,94
| 252,31
| 255,57
| |
| 224 36,5
| 357 06,5
| 4234,55
| - 2382,99
| 253,39
| 256,65
| |
| 224 41,0
| 357 11,0
| 4235,09
| - 2383,04
| 254,47
| 257,73
| |
| 224 46,5
| 357 16,5
| 4235,63
| - 2383,09
| 255,55
| 258,81
| |
| 224 51,0
| 357 21,0
| 4236,17
| - 2383,14
| 256,63
| 259,89
| |
| 224 56,5
| 357 26,5
| 4236,71
| - 2383,19
| 257,71
| 260,97
| |
| 225 01,0
| 357 31,0
| 4237,25
| - 2383,24
| 257,79
| 261,05
| |
| 225 06,5
| 357 36,5
| 4237,79
| - 2383,29
| 258,87
| 262,13
| |
| 225 11,0
| 357 41,0
| 4238,33
| - 2383,34
| 259,95
| 263,21
| |
| 225 16,5
| 357 46,5
| 4238,87
| - 2383,39
| 261,03
| 264,29
|
 , ,  .[1] .[1]
Таблица 2
Варианты индивидуальных задач для выполнения
контрольной работы 2 - «Теория погрешностей измерений»
| №
п/п
|
|
|
|
|
|
|
|
|
|
|
| |
|
| 39º16'00"
| + 2º30'
| 60º41,0'
| 26,25 га
| 175,10 м
| 5"
|
|
| 6; 4
| 10; 15
| |
|
| 16 03
| 1 45
| 42,0
|
|
|
|
|
| 4; 6
| 16; 14
| |
|
| 16 06
| 3 10
| 43,0
|
|
|
|
|
| 6; 10
| 18; 16
| |
|
| 16 09
| 3 00
| 40,0
|
|
|
|
|
| 10; 6
| 16; 18
| |
|
| 16 12
| 3 30
| 41,5
|
|
|
|
|
| 4; 10
| 10; 15
| |
|
| 16 15
| 3 45
| 42,5
|
|
|
|
|
| 10; 4
| 14; 16
| |
|
| 16 18
| 4 00
| 43,5
|
|
|
|
|
| 6; 4
| 16; 18
| |
|
| 16 21
| 4 12
| 40,5
|
|
|
|
|
| 4; 6
| 15; 10
| |
|
| 16 24
| 4 28
| 41,0
|
|
|
|
|
| 6; 10
| 14; 16
| |
|
| 16 27
| 4 35
| 42,0
|
|
|
|
|
| 10; 6
| 16; 18
| |
|
| 16 30
| 4 42
| 43,0
|
|
|
|
|
| 6; 10
| 15; 10
| |
|
| 16 33
| 4 50
| 40,0
|
|
|
|
|
| 4; 10
| 16; 14
| |
|
| 16 36
| 4 55
| 41,5
|
|
|
|
|
| 10; 4
| 18; 16
| |
|
| 16 39
| 5 00
| 42,5
|
|
|
|
|
| 6; 4
| 10; 14
| |
|
| 16 42
| 5 02
| 43,5
|
|
|
|
|
| 4; 6
| 14; 10
| |
|
| 16 45
| 5 05
| 40,5
|
|
|
|
|
| 6; 10
| 15; 10
| |
|
| 16 48
| 5 24
| 41,0
|
|
|
|
|
| 10; 6
| 10; 15
| |
|
| 16 51
| 5 17
| 42,0
|
|
|
|
|
| 4; 10
| 16; 18
| |
|
| 15 48
| 5 30
| 43,0
|
|
|
|
|
| 10; 4
| 18; 16
| |
|
| 15 51
| 5 32
| 40,0
|
|
|
|
|
| 6; 4
| 10; 15
| |
|
| 15 54
| 5 33
| 41,5
|
|
|
|
|
| 4; 6
| 16; 14
| |
|
| 15 57
| 5 35
| 42,5
|
|
|
|
|
| 6; 10
| 16; 18
| |
|
| 16 01
| 5 40
| 43,5
|
|
|
|
|
| 10; 6
| 10; 15
| |
|
| 16 04
| 5 42
| 40,5
|
|
|
|
|
| 4; 10
| 16; 18
| |
|
| 16 05
| 5 45
| 41,0
|
|
|
|
|
| 10; 4
| 14; 16
| |
|
| 16 10
| 5 47
| 42,0
|
|
|
|
|
| 6; 4
| 16; 14
| |
|
| 16 15
| 5 51
| 43,0
|
|
|
|
|
| 4; 6
| 15; 10
| |
|
| 16 20
| 5 53
| 40,0
|
|
|
|
|
| 6; 10
| 10; 15
| |
|
| 16 25
| 5 58
| 41,5
|
|
|
|
|
| 10; 5
| 16; 18
| |
|
| 16 28
| 6 01
| 42,5
|
|
|
|
|
| 4; 10
| 18; 16
| | | | | | | | | | | | | | | |
Данные для решения задач, номера которых не указаны в таблице, общие для всех студентов.
Таблица 3
Значения 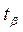 в зависимости от в зависимости от  и n -1 и n -1


| 0,9
| 0,95
| 0,98
| 0,99
| |
| 6,31
| 12,71
| 31,8
| 63,7
| |
| 2,92
| 4,30
| 6,96
| 9,92
| |
| 2,35
| 3,18
| 4,54
| 5,84
| |
| 2,13
| 2,77
| 3,75
| 4,60
| |
| 2,02
| 2,57
| 3,36
| 4,03
| |
| 1,943
| 2,45
| 3,14
| 3,71
| |
| 1,895
| 2,36
| 3,00
| 3,50
| |
| 1,860
| 2,31
| 2,90
| 3,36
| |
| 1,833
| 2,26
| 2,82
| 3,25
| |
| 1,812
| 2,23
| 2,76
| 3,17
| |
| 1,796
| 2,20
| 2,72
| 3,11
| |
| 1,782
| 2,18
| 2,68
| 3,06
| |
| 1,771
| 2,16
| 2,65
| 3,01
| |
| 1,761
| 2,14
| 2,62
| 2,98
| |
| 1,753
| 2,13
| 2,60
| 2,95
| |
| 1,746
| 2,12
| 2,58
| 2,92
| |
| 1,740
| 2,11
| 2,57
| 2,90
| |
| 1,734
| 2,10
| 2,55
| 2,88
| |
| 1,729
| 2,09
| 2,54
| 2,86
| |
| 1,725
| 2,09
| 2,53
| 2,84
| |
| 1,721
| 2,08
| 2,52
| 2,83
| |
| 1,717
| 2,07
| 2,51
| 2,82
| |
| 1,714
| 2,07
| 2,50
| 2,81
| |
| 1,711
| 2,06
| 2,49
| 2,80
| |
| 1,708
| 2,06
| 2,48
| 2,79
| |
| 1,706
| 2,06
| 2,48
| 2,78
| |
| 1,703
| 2,05
| 2,47
| 2,77
| |
| 1,701
| 2,05
| 2,47
| 2,76
| |
| 1,699
| 2,04
| 2,46
| 2,76
| |
| 1,697
| 2,04
| 2,46
| 2,75
|
Таблица 4
Варианты индивидуальных задач для выполнения контрольной работы 4 - «Уравнивание системы теодолитных ходов с одной узловой точкой»
| №
варианта
| Название линии
| Длина
линии, м
| Вершина угла
| Значение угла
| |
|
|
|
|
| |
| B–1
D–7
| 198,08
177,77
| B
D
| 168º 33,5'
181 08,0
| |
| 1–2
7–6
| 223,78
211,02
|
| 210 26,5
143 19,0
| |
| 2–3
6–5
| 198,79
222,55
|
| 193 02,5
219 51,0
| |
| 3–4
5–8
| 209,37
232,92
|
| 140 45,0
197 23,0
| |
| 4–5
8–F
| 172,49
228,54
|
| 240 49,5
151 56,5
| |
| 5–8
D–7
| 236,12
177,17
|
D
| 107 47,0
181 08,5
| |
| B–1
7–6
| 197,38
210,02
|
B
| 143 16,0
168 30,5
| |
| 6–5
1–2
| 221,75
223,08
|
| 219 46,0
210 23,5
| |
| 5–8
2–3
| 235,17
197,94
|
| 197 20,0
192 59,5
| |
| F–8
3–4
| 228,02
208,85
| F
| 205 47,5
140 41,5
| |
| 4–5
D–7
| 173,07
176,96
|
D
| 240 50,0
181 07,5
| |
| 5–8
7– 6
| 234,98
210,53
|
| 107 46,0
143 18,5
| |
| 8–F
6–5
| 227,95
222,93
|
| 151 57,5
219 51,5
| |
| B–1
5–8
| 197,26
236,01
| F
| 205 48,0
197 22,5
| |
| 1–2
8–F
| 223,92
228,33
| B
| 168 33,0
151 57,0
| |
| 2–3
D–7
| 198,86
177,45
|
F
| 210 27,0
205 47,0
| |
| 3–4
7–6
| 209,58
210,39
|
D
| 193 03,0
181 07,0
| |
| 4–5
6–5
| 172,59
222,82
|
| 140 44,0
143 19,5
| |
| 5–8
1–2
| 236,32
222,85
|
| 240 50,5
219 46,5
| |
| 8–F
2–3
| 227,82
198,46
|
| 107 46,5
151 55,5
| |
| B–1
D–7
| 198,08
177,77
|
| 107 46,5
151 55,5
| |
| 1–2
7–6
| 223,78
211,02
|
| 240 50,5
219 46,5
| |
| 2–3
6–5
| 198,79
222,55
|
| 140 44,0
143 19,5
| |
| 3–4
5–8
| 209,37
232,92
|
D
| 193 03,0
181 07,0
| |
| 4–5
8–F
| 172,49
228,54
|
F
| 210 27,0
205 47,0
| |
| 5–8
D–7
| 236,12
177,17
| B
| 168 33,0
151 57,0
| |
| B–1
7–6
| 197,38
210,02
| F
| 205 48,0
197 22,5
| |
| 6–5
1–2
| 221,75
223,08
|
| 151 57,5
219 51,5
| |
| 5–8
2–3
| 235,17
197,94
|
| 107 46,0
143 18,5
| |
| F–8
3–4
| 228,02
208,85
|
D
| 240 50,0
181 07,5
| |
| 4–5
D–7
| 173,07
176,96
| F
| 205 47,5
140 41,5
| |
| 5–8
7– 6
| 234,98
210,53
|
| 197 20,0
192 59,5
| |
| 8–F
6–5
| 227,95
222,93
|
| 219 46,0
210 23,5
| |
| B–1
5–8
| 197,26
236,01
|
B
| 143 16,0
168 30,5
| |
| 1–2
8–F
| 223,92
228,33
|
D
| 107 47,0
181 08,5
| |
| 2–3
D–7
| 198,86
177,45
|
| 240 49,5
151 56,5
| |
| 3–4
7–6
| 209,58
210,39
|
| 140 45,0
197 23,0
| |
| 4–5
6–5
| 172,59
222,82
|
| 193 02,5
219 51,0
| |
| 5–8
1–2
| 236,32
222,85
|
| 210 26,5
143 19,0
| |
| 8–F
2–3
| 227,82
198,46
| B
D
| 168º 33,5'
181 08,0
| |
| B–1
D–7
| 198,08
177,77
|
| 107 46,5
151 55,5
| |
| 2–3
6–5
| 198,79
222,55
|
| 140 44,0
143 19,5
| |
| 5–8
D–7
| 236,12
177,17
| B
| 168 33,0
151 57,0
| |
| 5–8
2–3
| 235,17
197,94
|
| 107 46,0
143 18,5
| |
| 5–8
7– 6
| 234,98
210,53
|
| 197 20,0
192 59,5
| |
| 1–2
8–F
| 223,92
228,33
|
D
| 107 47,0
181 08,5
| |
| 4–5
6–5
| 172,59
222,82
|
| 210 26,5
143 19,0
| |
| B–1
D–7
| 198,08
177,77
|
| 240 49,5
151 56,5
| |
| 3–4
5–8
| 209,37
232,92
|
| 219 46,0
210 23,5
| |
| B–1
7–6
| 197,38
210,02
|
D
| 240 50,0
181 07,5
|
Таблица 5
Исходные данные
| №
пунктов
| Координаты, м
| | Х
| Y
| | A
B
C
D
E
F
| +4519,83
4584,11
6014,73
5612,65
4858,23
4897,84
| +5204,38
5462,18
6171,34
6165,08
7006,76
6685,61
|
ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Производная – этопредел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называется дифференцированием
 , ,
где  – приращение функции на величину – приращение функции на величину  . .
Частной производной функции нескольких переменных по одной из этих переменных называется производная, взятая по этой переменной при условии, что все остальные переменные временно постоянны. Для функции двух переменных z = f(x, y) частной производной по переменной x называется производная этой функции по x при постоянном y. Обозначается частная производная по x следующим образом: 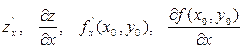
Аналогично частной производной функции z = f(x, y) по переменной y называется производная этой функции по y при постоянном x. Обозначения:  . .
Выполнение заданий предполагает безусловное знание следующих основных правил дифференцирования.
1. Производная суммы дифференцируемых функций равна сумме производных:
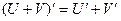 . .
2. Постоянный множитель можно выносить за знак производной:
 , ,
где C – const.
3. Если  и и  - дифференцируемые функции, то существует производная их произведения, которая вычисляется по формуле: - дифференцируемые функции, то существует производная их произведения, которая вычисляется по формуле:
 . .
4. Если  и и  - дифференцируемые функции, то существует производная частного, которая вычисляется по формуле: - дифференцируемые функции, то существует производная частного, которая вычисляется по формуле:
 , ,  . .
Для эффективного дифференцирования сложных функций полезна таблица 3.1. основных элементарных функций, аргумент которых есть тоже функция. Итак, пусть 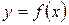 , где , где  . Тогда . Тогда
1. 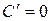 , C – const , C – const
| 2.  , n – const , n – const
| 3. 
| 4. 
| 5. 
| 6. 
| 7. 
| 8. 
| 9. 
| 10. 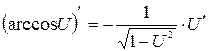
| 11. 
| 12. 
| 13.  , ,  , ,  ,
a – const ,
a – const
| 14. 
| 15.  , ,  , ,  ,
a – const ,
a – const
| 16. 
|
Таблица 3.1.
Пример.
Дана функция  . Найти . Найти  и и  . .
Решение. 
 ; ;
 . .
[1] Координаты т. 216 одинаковые для всех вариантов.
|



 º ′
º ′
 º ′
º ′
 ,
м
,
м
 ,
м
,
м
 ,
м
,
м
 ,
м
,
м
 ,
,  .[1]
.[1]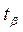 в зависимости от
в зависимости от  и n -1
и n -1

 ,
, – приращение функции на величину
– приращение функции на величину  .
.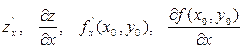
 .
.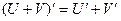 .
. ,
, и
и  - дифференцируемые функции, то существует производная их произведения, которая вычисляется по формуле:
- дифференцируемые функции, то существует производная их произведения, которая вычисляется по формуле: .
. ,
,  .
.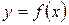 , где
, где  . Тогда
. Тогда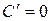 , C – const
, C – const
 , n – const
, n – const







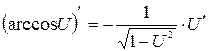


 ,
,  ,
,  ,
a – const
,
a – const

 ,
, 
 . Найти
. Найти  и
и  .
.
 ;
; .
.


