Заглавная страница
Избранные статьи
Случайная статья
Познавательные статьи
Новые добавления
Обратная связь
FAQ
Написать работу

ТОП 10 на сайте

Приготовление дезинфицирующих растворов различной концентрации

Техника нижней прямой подачи мяча.

Франко-прусская война (причины и последствия)

Организация работы процедурного кабинета

Смысловое и механическое запоминание, их место и роль в усвоении знаний

Коммуникативные барьеры и пути их преодоления

Обработка изделий медицинского назначения многократного применения

Образцы текста публицистического стиля

Четыре типа изменения баланса

Задачи с ответами для Всероссийской олимпиады по праву

Мы поможем в написании ваших работ!

ЗНАЕТЕ ЛИ ВЫ?

Влияние общества на человека

Приготовление дезинфицирующих растворов различной концентрации

Практические работы по географии для 6 класса

Организация работы процедурного кабинета

Изменения в неживой природе осенью

Уборка процедурного кабинета

Сольфеджио. Все правила по сольфеджио

Балочные системы. Определение реакций опор и моментов защемления

Главная Избранные Случайная статья Познавательные Новые добавления Обратная связь FAQ Написать работу

Богомаз И.В., Воротынова О.В.

↑

Стр 1 из 5Следующая ⇒

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

Федеральное государственное образовательное учреждение

высшего профессионального образования

«Сибирский федеральный университет»

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

Сборник контрольных заданий для самостоятельной работы студентов заочной формы обучения

Богомаз И.В., Воротынова О.В.

Учебно-методическое пособие для самостоятельной работы

студентов заочной формы обучения

направление 270100 «Строительство»

Красноярск

ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ

При изучении учебного курса «Теоретическая механика» студент – заочник знакомится с математическими моделями реальных явлений и существующими методами расчета, которые базируются на знаниях, полученных при изучении аналитической геометрии и линейной алгебры, векторной алгебры, высшей алгебры, основ математического анализа и приведены в таблице 1.

Таблица 1.

Наименование дисциплины	Раздел	Тема
Математика	Аналитическая геометрия и линейная алгебра	Алгебраические преобразования, решение алгебраических уравнений первого и второго порядка, Евклидова геометрия, тригонометрия, функции и графики аналитических и трансцендентных функций.
Векторная алгебра	Системы координат, преобразование систем координат, понятие вектора и линейные операции над ним, проекции векторов на оси, геометрическое и аналитическое сложение векторов, скалярное и векторное произведения векторов, решение векторных уравнений, кривые второго порядка, параметрическое задание функций.
Высшая алгебра	Системы линейных уравнений, определители, квадратичные формы, Евклидовы пространства, вычисление корней многочленов.
Основы математического анализа	Дифференцирование функций, экстремумы функций, геометрические приложения производных, неопределенный и определенный интегралы, дифференциальные уравнения, ряды.

Основным документом, определяющим необходимый объём знаний студентов, является программа курса, составленная на основе государственного образовательного стандарта высшего профессионального образования.

Процесс овладения студентами определенных знаний и навыков, складывается из самостоятельного изучения соответствующих разделов курса по учебникам, самостоятельного выполнения контрольных работ. Каждый студент – заочник обязан защитить контрольные работы и получить допуск к экзамену.

Настоящие методические указания по основным темам программы учебного курса «Теоретическая механика» составлены применительно к учебному пособию , подготовленному на кафедре.

Основная и дополнительная литература по изучению учебного курса «Теоретическая механика»

Основная

1. Богомаз И. В. Теоретическая механика. Том 1. Кинематика. Статика: Тексты лекций. – М.: Изд-во АСВ, 2005. – 190 с., 176 илл.

2. Богомаз И. В. Теоретическая механика. Том 2. Динамика. Аналитическая механика: Тексты лекций. – М.: Изд-во АСВ, 2005. – 143 с., 91 илл.

3. Богомаз И.В., Новикова Н.В. Теоретическая механика. Кинематика. Статика: сборник задач. – Красноярск: ИПК СФУ, 2009. – 174 с.

4. Богомаз И.В., Воротынова О.В., Новикова Н.В., Чабан Е.А. Теоретическая механика. Динамика. Аналитическая механика: сборник задач. - Красноярск: ИПК СФУ, 2009. – 152 с.

5. Яблонский А. А. Курс теоретической механики: Учебник для вузов: В 2 ч. – М.: Высш. шк., 1984. – Ч. 1,2. – 343 с., 423 с.

6. Тарг С. М. Курс теоретической механики: Учебник для втузов. – М.: Высш. шк., 1995. – 416 с.

7. Мещерский И.В. Сборник задач по теоретической механике. – М: Наука, 1986. - 448 с.

Дополнительная

8. Никитин Н.Н. Курс теоретической механики: Учебник. – М.: Высш. шк., 1990. – 607 с.

9. Бутенин Н.В. Курс теоретической механики: Учебник для втузов: В 2 т., Т. 1,2. – М.: Высш. шк., 1985.

10. Теоретическая механика в примерах и задачах. Статика. Кинематика. Ч. 1: Учеб. пособ. для студентов технических вузов / Под ред. М.И.

Бать. – СПб.: Политехника, 1995. – 670 с.

Программа учебного курса «Теоретическая механика»

Разбита на четыре модуля: модуль I «кинематика», модуль II «статика», модуль III «динамика », модуль IV «аналитическая механика».

Модуль I. КИНЕМАТИКА

1. Предмет кинематики. Основные понятия, задачи кинематики. Пространство и время в классической механике. Относительность механического движения. Система отсчета. Кинематика точки. Траектория, скорость, ускорение точки. Векторный способ задания движения точки. Векторы скорости и ускорения точки (годограф скорости). Координатный способ задания движения. Определение скорости и ускорения точек по их проекциям на координатные оси. [1, 3, 5, 6, 8, 9, 10]

2. Естественный способ задания движения точки – определения. Оси естественного трехгранника. Скорость и ускорение точки в проекциях на оси естественного трехгранника, касательное и нормальное ускорение точки. Скорость точки в полярных координатах; ускорение точки в полярных координатах. Простейшие движения твердого тела. Основная теорема кинематики. [1, 3, 5, 6, 8, 9, 10]

3. Поступательное движение твердого тела. Теорема о траекториях, скоростях и ускорениях точек твердого тела при поступательном движении. [1, 3, 5, 6, 8, 9, 10]

4. Вращательное движение твердого тела вокруг неподвижной оси. Угол поворота, угловая скорость, угловое ускорение. Уравнение вращательного движения тела. [1, 3, 5, 6, 8, 9, 10]

5. Скорость и ускорение точек твердого тела при его вращении вокруг неподвижной оси. Преобразование простейших движений. Векторы угловой скорости и углового ускорения тела. Выражение скорости точки

вращающегося тела и ее касательного и нормального ускорений в виде векторных произведений (уравнения Эйлера). [1, 3, 5, 6, 8, 9, 10]

6. Сложное движение точки. Основные понятия – абсолютное, относительное и переносное движения. Теорема о сложении скоростей. Сложение скоростей точки в общем случае переносного движения. Сложение ускорений точки в общем случае переносного движения. Ускорение Кориолиса. Правило Жуковского. [1, 3, 5, 6, 8, 9, 10]

7. Плоскопараллельное (плоское) движение твердого тела. Уравнения движения плоской фигуры (разложение плоского движения на поступательное движение вместе с полюсом и вращательное вокруг полюса). Скорости точек твердого тела при плоскопараллельном движении – теорема. Мгновенный центр скоростей – терема. Определение скоростей точек плоской фигуры (мгновенно-поступательное и мгновенно-вращательное движение). [1, 3, 5, 6, 8, 9, 10]

8. Ускорение при плоскопараллельном движении твердого тела – теорема. Основные способы вычисления углового ускорения при плоском движении, аналитический и геометрический способы. [1, 3, 5, 6, 8, 9, 10]

Модуль II. СТАТИКА

1. Введение в статику (история науки). Предмет изучения. Основные понятия: материальная точка, абсолютно твердое тело, механическая система. Сила, система сил, система сил эквивалентная нулю, уравновешенная система сил, равнодействующая системы сил, силы внешние и внутренние. Исходные положения (аксиомы) статики. Связи и реакции связей [1, 3, 5, 6, 8, 9, 10].

2.Система сходящихся сил.Приведение к равнодействующей. Геометрический и аналитический способы сложения сил. Условия равновесия системы сходящихся сил. Геометрические и аналитические

условия равновесия. Теорема о трех непараллельных силах. Примеры. [1, 3, 5, 6, 8, 9, 10]

3. Параллельные силы. Приведение к равнодействующей двух сил, направленных в одну сторону. Приведение к равнодействующей двух сил, направленных в разные стороны. [1, 3, 5, 6, 8, 9, 10]

4. Теория пар сил. Пара сил. Векторный момент пары сил. Основные теоремы. Сложение пар сил в плоскости и пространстве. Условия равновесия пар сил. Метод сечения. [1, 3, 5, 6, 8, 9, 10]

5. Момент силы. Момент силы относительно центра и оси. Момент силы относительно точки в плоскости. Приведение силы к заданному центру. Теорема Пуансо. Главный вектор и главный момент системы сил. Плоская система сил. Теорема Вариньона о моменте равнодействующей системы сходящихся сил. Приведение плоской системы сил к простейшему виду. Частные случаи приведения плоской системы сил к заданному центру. [1, 3, 5, 6, 8, 9, 10]

6. Условия равновесия сил. Система сил, произвольно расположенных на плоскости. Условия равновесия произвольной системы сил. Равновесие плоской системы сил (основная форма условий равновесия). Реакция заделки. Вторая форма условий равновесия. Третья форма условий равновесия (уравнения трех моментов). Пространственная заделка. [1, 3, 5, 6, 8, 9, 10]

7. Равновесие системы твердых тел. Определение реакций опор составных конструкций. Устойчивость тел при опрокидывании. Рычаг. [1, 3, 5, 6, 8, 9, 10]

8. Плоские стержневые фермы. Общая характеристика и классификация ферм. Определение усилий в стержнях простейших ферм. Способ сплошных сечений (способ Риттера, или способ моментной точки). Способ проекций (способ вырезания узлов). [1, 3, 5, 6, 8, 9, 10]

9.Равновесие при наличии сил трения. Трение скольжения при покое (сцепление) и при движении. Коэффициент трения. Закон Амонтона -

Кулона. Угол и конус трения. Область равновесия. Трение гибкой нити о цилиндрическую поверхность. Трение качения; коэффициент трения качения. [1, 3, 5, 6, 8, 9, 10]

10. Частные случаи пространственной системы сил. Изменение главного момента при перемене центра приведения. Инварианты системы. Частные случаи приведения пространственной системы сил. Динамический винт. Уравнение центральной линии. [1, 3, 5, 6, 8, 9, 10]

11. Центр параллельных сил и центр тяжести. Центр параллельных сил. Центр тяжести твердого тела. Методы определения центров тяжести. Центр тяжести простейших тел. Статические моменты и центр тяжести. [1, 3, 5, 6, 8, 9, 10]

Модуль III. ДИНАМИКА

1. Предмет динамики. Основные понятия и определения: масса, сила, постоянные и переменные силы. Инерциальная система отсчета. Основные аксиомы классической механики. Системы единиц. Задачи динамики. Дифференциальные уравнения движения материальной точки в системе декартовых прямоугольных координат и проекциях на оси естественного трехгранника. Две основные задачи динамики.

Первая задача динамики. Вторая задача динамики. Постоянные интегрирования и их определение по начальным условиям. Основные виды прямолинейного и криволинейного движения точки (движение точки с учетом и без учета сопротивления среды). [2, 4, 5, 6, 8, 9]

2. Механическая система. Масса системы. Геометрия масс: центр масс системы и его координаты; моменты инерции, моменты инерции относительно точки и оси; теорема Гюйгенса – Штейнера. Моменты инерции простейших однородных тел: однородный стержень, прямоугольная пластина, круглый диск, круглый цилиндр, шар. Радиус инерции. [2, 4, 5, 6, 8, 9].

3. Классификация сил, действующих на механическую систему: внешние и внутренние силы. Свойства внутренних сил. Дифференциальные законы движения механической системы. Теорема о движении центра масс. Закон сохранения центра масс. Главный вектор количеств движения механической системы. Теорема об изменении главного вектора количеств движения механической системы и ее применение к сплошной среде (теорема Эйлера). Закон сохранения количества движения.

Главный момент количеств движения, или кинетический момент механической системы относительно центра и оси. Кинетический момент вращающегося твердого тела относительно оси вращения. Теорема об изменении кинетического момента механической системы. Закон сохранения кинетического момента системы [2, 4, 5, 6, 8, 9].

4. Элементарная работа силы: ее аналитическое выражение. Работа силы на конечном пути. Работа силы тяжести, силы упругости, силы тяготения. Работа и мощность сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси. Работа сил, приложенных к твердому телу, при поступательном, вращательном и плоскопараллельном движениях. Равенство нулю суммы работ внутренних сил, действующих в твердом теле или в неизменяемой механической системе.

Понятие о силовом поле. Потенциальное силовое поле и силовая функция. Выражение проекций силы через силовую функцию. Примеры вычисления силовых функций. Работа силы на конечном перемещении точки в потенциальном силовом поле. Потенциальная энергия. Силовая функция и потенциальная энергия системы [2, 4, 5, 6, 8, 9].

5. Кинетическая энергия механической системы. Вычисление кинетической энергии твердого тела в различных случаях его движения. Теорема об изменении кинетической энергии механической системы. Закон сохранения механической энергии [2, 4, 5, 6, 8, 9].

6. Принцип Даламбера для материальной точки; сила инерции. Принцип Даламбера для механической системы. Главный вектор и главный

момент сил инерции. Приведение сил инерции твердого тела к центру. Определение с помощью принципа Даламбера динамических реакций при вращении твердого тела вокруг неподвижной оси. Статическая и динамическая уравновешенность [2, 4, 5, 6, 8, 9].

7. Дифференциальные законы поступательного движения твердого тела. Дифференциальные законы вращательного движения твердого тела вокруг неподвижной оси. Математический и физический маятники. Опытное определение моментов инерции тел. Дифференциальные законы плоского движения твердого тела. Примеры [2, 4, 5, 6, 8, 9].

Общие методические указания

Перечень задач, входящих в контрольные работы приведён в таблице 2. Студенты всех специальностей выполняют контрольные работы по каждому модулю.

Таблица 2

Модули	Контрольные работы	Задачи
1 часть Модуль № 1 Модуль № 2	1 часть № 1 № 2 № 3	1, 2, 3*. 1. 1, 2, 3.
2 часть Модуль № 3 Модуль № 4	2 часть № 4 № 5 № 6	1, 2. 1*, 2. 1.

Примечание: задачи и задания, отмеченные звездочкой (*), студентами ускоренной формы обучения не выполняются.

Теоретическая механика – одна из дисциплин, где изучение каждой темы должно обязательно сопровождаться самостоятельным решением студентом ряда задач. Очень важным при изучении курса является систематическое последовательное изучение предмета.

Для этого необходимо:

1. Написать краткий конспект каждой лекции из [1,2] чтобы к концу изучения иметь краткий курс лекций по теоретической механике.

2. Для закрепления пройденной темы необходимо решить ряд задач, рекомендованных для самостоятельной работы [3, 4]– это способствует лучшему пониманию и усвоению пройденного материала.

Каждый студент выполняет четыре контрольные работы. При этом:

· не следует приступать к выполнению задания, не изучив теорию соответствующей темы;

· каждая контрольная работа выполняется на белой бумаге формата А4 (297´420 мм) с полями 20 мм слева и 5 мм с других сторон, листы

задания должны быть подшиты по центру с левой стороны, титульный лист оформляется согласно рис. 1.

Контрольную работу необходимо оформить аккуратно, с выполнением правил и требований строительного черчения и с использованием чертежных инструментов.

Исходные численные данные к задачам студент выбирает самостоятельно из таблиц, которые прилагаются к каждой задаче.

Исходные данные для индивидуальных заданий на контрольные работы студент должен взять из приводимых далее таблиц в строгом соответствии со своим личным номером (номер зачетной книжки). Для этого необходимо выписать номер зачетной книжки и под последними 6-ью цифрами подписать буквы: а, б, в, г, д, е.

Пример. При номере 0305 107:


	а	б	в	г	д	е

Перед решением задачи индивидуального задания необходимо выписать для заданного варианта полное условие с числовыми данными, написать текст задания, составить аккуратный чертеж с соблюдением масштаба и показать на нем все размеры в числах.

Каждый этап решения задач должен быть озаглавлен.

При выполнении расчетов сначала записывается формула, затем в нее подставляются исходные данные с размерностями системы Си и подсчитывается результат. Например:

Решение должно сопровождаться краткими, последовательными и грамотными, без сокращения слов, объяснениями и чертежами, на которых должны быть показаны все размеры в числах. Необходимо указывать

единицы измерения (размерность) всех полученных результатов. Задание, выполненное небрежно, без соблюдения всех перечисленных требований, не принимается.

Сдача и защита контрольных работ производится во время сессии, в сроки, установленные графиком учебного процесса в следующем порядке:

· преподаватель проверяет готовые задания, указывает на ошибки, если они имеются и задает несколько вопросов по теме выполненного задания;

· для защиты задания студенту дается задача по этой теме в виде контрольной работы;

· задание не засчитывается, если студент не смог решить задачу. Только после дополнительного изучения темы он может повторно защитить задание.

Типовые задачи для защиты представлены в [3, 4].

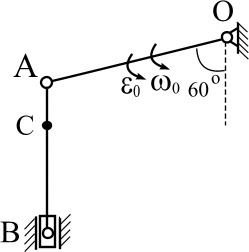
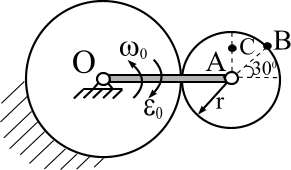
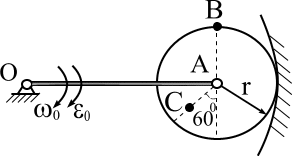
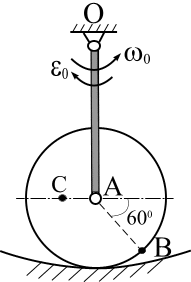
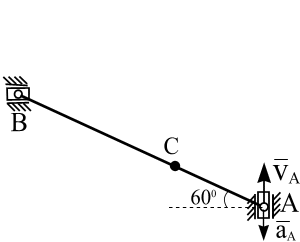
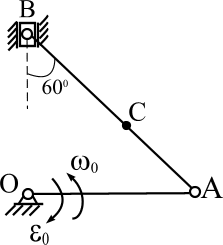
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Сибирский федеральный университет» ИСИ Кафедра «Автомобильные дороги и городские сооружения» Контрольная работа № по теоретической механике тема задания_________________ ____________________________ выполнил студент (ка)_________гр. Ф. И. О. _______________________ Проверил______________________ «___» __________________ 200 г. Красноярск 201 г.

Рис. 1.

МОДУЛЬ 1. КИНЕМАТИКА

Контрольная работа № 1.

Таблица 7

В таблице 7 введены обозначения: u_A - скорость точки А, а_А- ускорение точки А, w_о- угловая скорость звена ОА, e_o- угловое ускорение звена ОА.

№ варианта	Размеры, см	w_о, c^-1	e_o, c^-2	u_A, см/с	а_А, см/с²
ОА	r	АВ	АС
			-				-	-
		-	-				-	-
			-				-	-
			-				-	-
		-					-	-
		-	-				-	-
		-					-	-
	-	-			-	-
	-	-			-	-
	-	-			-	-
		-					-	-
	-	-			-	-
		-					-	-
			-				-	-
	-		-		-	-
			-				-	-
			-				-	-
			-				-	-
		-					-	-
		-					-	-
			-				-	-
	-	-			-	-
		-					-	-

Продолжение таблицы 7
	-	-		-	-
		-				-	-
		-				-	-
	-		-	-	-
		-				-	-

Таблица 8

1.	3.
2.	4.

Продолжение таблицы 8
5.	8.
6.	9.
7.	10.

Продолжение таблицы 8
11.	15.
12.	16.
13.	17.
14.	18.

Продолжение таблицы 8

19.	22.
20.	23.
21.	24.

Продолжение таблицы 8
25.	27.
26.	0.