Розгалуження в алгоритмах і програмах

Пригадайте!

1. Що таке алгоритм? Назвіть основні блоки блок-схеми алгоритму і поясніть їх призначення.

2. Які алгоритми (фрагменти алгоритмів) називаються лінійними? У чому полягає їх характерна особливість?

3. Які вирази називаються логічними? Які значення вони можуть набувати?

4. Назвіть логічні операції, наведіть означення кожної з них.

5. Назвіть логічні функції табличного процесора Excel 2007. Чому дорівнюють їхні значення залежно від значень аргументів.

Алгоритми з розгалуженням

У попередніх пунктах було розглянуто кілька лінійних алгоритмів, зокрема, алгоритми для розв’язування задач на обчислення значень арифметичного виразу для виконавця, який вміє виконувати арифметичні операції. Розглянемо приклад задачі, алгоритм розв’язування якої – не є лінійним.

Задача 1. Обчислити значення виразу (a – b) / (c – d), де a, b, c, d – дійсні числа.

 

Звернемо увагу на те, що значення цього виразу можна обчислити не для будь-якого набору значень змінних a, b, c, d. Адже цей вираз містить дію ділення на вираз зі змінними, значення якого може дорівнювати нулю. Тобто якщо значення різниці c – d дорівнює нулю, то значення виразу (a – b) / (c – d) обчислити не можна, а якщо не дорівнює – то можна.

Це означає, що система команд виконавця повинна містити команду порівняння двох чисел, наприклад таку: «s=t?», де s і t – або числа, або змінні чи вирази, які мають певні числові значення. Така команда є прикладом команди перевірки умови. Результатом виконання команди перевірки умови може бути або істина (умова виконується), або хиба (умова не виконується).

З іншого боку, ви вже знаєте, що порівняння «s=t?» можна розглядати як висловлення або як простий логічний вираз, який набуватиме значення true або false залежно від конкретних значень змінних s і t. І тоді команду перевірки умови можна інтерпретувати як команду обчислення значення логічного виразу.

Алгоритм розв’язування задачі 1 виглядатиме так:

1. Увести значення змінних a, b, c, d.

2. х:= c – d.

3. Обчислити значення логічного виразу х = 0.

4. Якщо обчислене значення логічного виразу true, то повідомити «Вираз значення не має: ділення на нуль», після чого виконати команду 8, якщо false – то виконати команду 5.

5. у:= a – b.

6. z:= у/х.

7. Повідомити значення змінної z.

8. Закінчити виконання алгоритму.

 

Команди 1–3 наведеного алгоритму виконуватимуться про будь-якому наборі значень змінних a, b, c, d. Подальше виконання цього алгоритму залежатиме від значення логічного виразу, обчисленого в команді 3. Якщо це значення true, то виконуватимуться команди 5–8, а якщо false, то виконуватимуться команда виведення повідомлення «Вираз значення не має: ділення на нуль» і команда 8.

У блок-схемі алгоритму команди перевірки умови або обчислення значення логічного виразу позначаються блокомРішення . Оскільки результатом виконання цих команд може бути або true або false, то з цього блоку є два виходи. Вихід Так означає, що результатом перевірки умови є true, а вихід Ні – що результатом перевірки умови є false.

Наведемо блок-схему наведеного вище алгоритму розв’язування задачі 1 (рис. 2.46).

 

 

Рис. 2.46. Блок-схема алгоритму обчислення значення виразу (a – b) / (c – d)

 

Розглянемо фрагмент алгоритму на рис. 2.46 від блоку Рішення до блоку Термінатор (не включаючи цей блок).

Характерною рисою цього фрагменту алгоритму є те, що при кожному його виконанні деякі команди будуть виконуватися, причому кожна по одному разу, а деякі – виконуватися не будуть. Це залежить від результату виконання команди перевірки умови (команди обчислення значення логічного виразу).

Такий фрагмент алгоритму називається розгалуженням.

 

Виконаємо наведений алгоритм для двох наборів даних. Ці набори підберемо так, щоб проілюструвати хід виконання алгоритму для кожного з двох можливих результатів обчислення значення логічного виразу.

Команда	Результат виконання
Виконання для першого набору даних
Увести значення змінних a, b, c, d	a = 5; b = 6; c = –3; d = 5
х:= c – d	х = –3 – 5 = –8
Обчислити значення логічного виразу х = 0	(-8 = 0) = false
у:= a – b	у = 5 – 6 = –1
z:= у/х	z = –1/(–8) = 0,125
Повідомити значення змінної z	z = 0,125
Виконання для другого набору даних
Увести значення змінних a, b, c, d	a = 12,3; b = –1; c = 8,2; d = 8,2
х:= c – d	х = 8,2 – 8,2 = 0
Обчислити значення логічного виразу х = 0	(0 = 0) = true
Повідомити: «Вираз значення не має: ділення на нуль»	Повідомлення: «Вираз значення не має: ділення на нуль»

 

Звертаємо вашу увагу:

• наведений алгоритм містить як розгалуження, так і лінійні фрагменти;
• у розгалуженнях можна використовувати як прості логічні вирази, так і складені.

 

В алгоритмах використовують розгалуження двох видів: повне розгалуження (рис. 2.47) і неповне розгалуження (рис. 2.48)

Рис. 1.7. Повне розгалуження

 

 

До верстальника: на рис 2.47 і 2.48 у ромбах вставити такі тексти: Перевірка умови (обчислення значення логічного виразу)

 

 

Виконання повного розгалуження відбувається так: виконавець виконує команду перевірки умови (команду обчислення значення логічного виразу); якщо результат виконання цієї команди true, то виконавець виконує послідовність команд 1, після чого переходить до виконання першої команди наступного фрагмента алгоритму; якщо ж результат виконання цієї команди false, то виконавець виконує послідовність команд 2, після чого також переходить до виконання першої команди наступного фрагмента алгоритму.

Виконання неповного розгалуження відрізняється від виконання повного розгалуження тим, що при результаті виконання команди перевірки умови false, виконавець одразу переходить до виконання першої команди наступного фрагмента алгоритму.

 

Усередині розгалуження можуть знаходитися як лінійні фрагменти алгоритму, так і інші розгалуження. Наведемо приклад алгоритму із розгалуженням у розгалуженні.

 

Задача 2. Дано два числа. Визначити, чи рівні вони. Якщо ні, то яке з них більше.

 

Блок-схема алгоритму розв’язування цієї задачі виглядатиме так (рис. 2.49):

 

 

Наведемо приклад ще однієї задачі, алгоритм розв’язування якої містить розгалуження.

Задача 3. Є дев’ять однакових на вигляд монет, одна з яких фальшива і легша від інших. Двома зважуваннями на терезах без гир визначити фальшиву монету.

Складемо алгоритм для виконавця з такою системою команд:

1. Узяти вказану купку монет.

2. Розділити вказану купку монет на три рівні купки.

3. Покласти на терези вказані купки монет.

4. Перевірити умову «Терези в рівновазі?».

5. Визначити при зважуванні, яка з купок монет легша.

6. Повідомити результат.

 

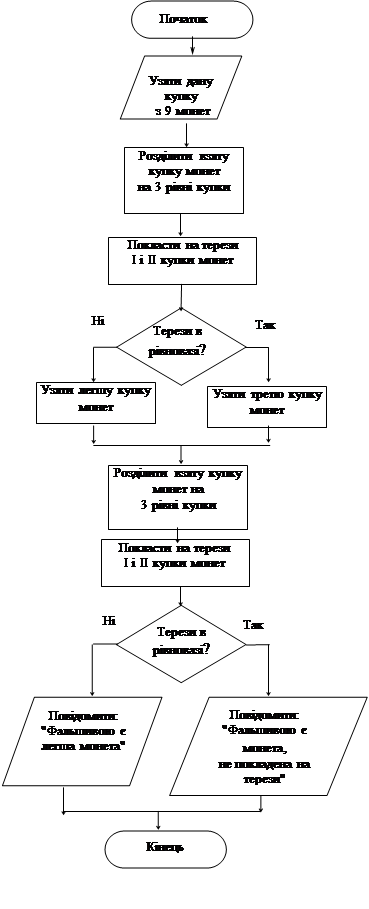
Для виконавця із такою системою команд алгоритм розв’язування задачі 3 такий:

1. Узяти дану купку з 9 монет.

2. Розділити взяту купку монет на три рівні купки.

3. Покласти на терези першу і другу купки монет.

4. Перевірити умову «Терези в рівновазі?».

5. Якщо істина, то взяти третю купку монет, якщо хиба, то взяти легшу купку.

6. Розділити взяту купку монет на три рівні купки.

7. Покласти на терези першу і другу купки монет.

8. Перевірити умову «Терези в рівновазі?».

9. Якщо істина, то повідомити: "Фальшивою є монета, що залишилася не покладеною на терези", якщо хиба — повідомити: "Фальшивою є легша монета".

Блок-схема цього алгоритму виглядатиме так (рис. 2.50):

 

 

 

Рис. 2.50. Блок-схема алгоритму розв’язування задачі 3