
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потенциометрические датчики давленияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
В таких датчиках используется потенциометрический преобразователь перемещений. Эта конструкция является унифицированной: при переходе от одного диапазона измерений к другому так выбирается толщина мембраны, что её максимальный прогиб не изменяется.
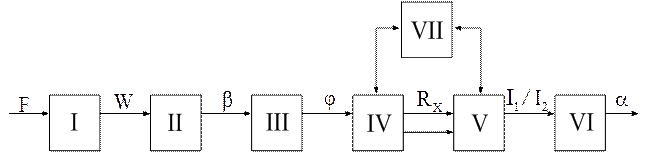
Рис. 1.1. Структурная схема прибора
Структурную схему ЭДМУ можно представить в виде семи звеньев. Первые четыре звена относятся к датчику; два последующих - к указателю, звено VII - источник питания. Кинематическая схема датчика приведена на рис. 1.2.
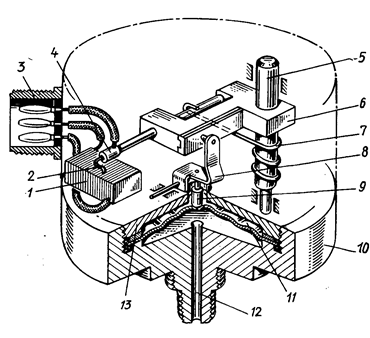
Рис. 2. Потенциометрический датчик давления 1 – потенциометр; 2 – щетка; 3 – вилка; 4 – щеткодержатель; 5 – ось поводка; 6 – поводок; 7 – возвратная пружина; 8 – качалка; 9 – шток; 10, 13 – основания; 11 – мембрана; 12 – штуцер.
Упругий чувствительный элемент - мембрана - является первым звеном. Под действием разности давлений (P1-P2) центр мембраны перемещается на величину W. Статической характеристикой мембраны является зависимость
где C1 - коэффициент, учитывающий геометрические размеры и форму гофрировки мембраны; EM - модуль упругости мембраны, н/м; (P1- P2) - измеряемая разность давлений. Звеном II является рычаг 8. Статическая характеристика звена II на рабочем участке может быть линейной и описана уравнением прямой
где СII - коэффициент пропорциональности, рад/м; W – перемещение толкателя, м; β - угол отклонения конца рычага 5, рад.
Звеном III датчика служит поводок 6 передаточно - множительного механизма. Статическая характеристика этого звена также может быть принята линейной и представлена в виде
где СIII - коэффициент пропорциональности звена III; j - угол отклонения рычага 6 со щеткой 2.
Звеном IV является потенциометрический преобразователь. Статической характеристикой звена является зависимость
где CIV - коэффициент пропорциональности звена; RX - сопротивление участка потенциометрического преобразователя. Общая статическая характеристика датчика, без учета сравнительно малой упругости спиральной пружины 7, имеет вид
Звено V - мостовая схема манометра (рис.1.3). Статическая характеристика звена
Рис. 1.3.Принципиальная схема манометра: 1-чувствительный элемент; 2-щетка; 3-магнит неподвижный; 4-магнит подвижный.
Если с целью симметрии мостовой схемы предположить R1=R2, то статическую характеристику можно записать в виде
где r - сопротивление рамки.
Подставив в полученное выражение
VI звеном структурной схемы электромеханического манометра ЭДМУ является логометр с подвижным магнитом. Статической характеристикой логометра с подвижным магнитом является зависимость
где n1 и n2 - числа витков катушек; k - коэффициент, учитывающий форму и размеры катушек; b - угол между катушками; I1 и I2 - токи в катушках.
Общая статическая характеристика шести звеньев, найденная в результате решения системы уравнений, имеет вид сложной функции:
где Функция не линейна, но при правильном выборе параметров электрической схемы и деталей механических звеньев удается получить шкалу манометра с практически равномерной градуировкой в рабочем диапазоне. С целью компенсации температурных погрешностей, вызванных влиянием температуры q окружающей среды на рамки логометра, сопротивление полудиагонали выполняется из двух сопротивлений R3 и R4, первое из которых - с положительным температурным коэффициентом, а второе - с нулевым температурным коэффициентом (например, манганиновое). Выберем величину сопротивления полудиагонали
где a1 и a2 - температурные коэффициенты сопротивлений; R'30 - сумма сопротивлений медной и манганиновой катушки при нормальной температуре. Подставляя эти выражения в статическую характеристику и считая, что остальные сопротивления не зависят от окружающей температуры, получим
где
Если принять
то отношение токов
Следовательно, соотношение (1.14) и является условием температурной компенсации. Подставив в выражение (1.12) значения коэффициентов A1, В1, A2 и B2, можно определить необходимую для компенсации величину сопротивления медной катушки R30.
Полная компенсация температурной ошибки может быть достигнута только при определении значений сопротивлений RX и RY. При других значениях RX и RY появится температурная ошибка, но эта ошибка значительно меньше той, которая была бы при отсутствии компенсации. При R1 = R2 и RX = RY, благодаря симметрии схемы, температурная ошибка равна нулю даже без компенсации. Поэтому при расчете сопротивлений Rзо условие полной компенсации целесообразно брать для значений RX и RY, соответствующих положению щетки на расстоянии приблизительно 20-30% от края потенциометра.
|
||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 424; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.18.192 (0.01 с.) |

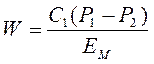 (1.1)
(1.1)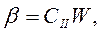 (1.2)
(1.2)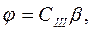 (1.3)
(1.3)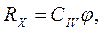 (1.4)
(1.4)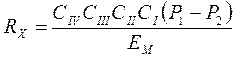 (1.5)
(1.5)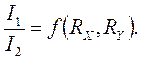 (1.6)
(1.6)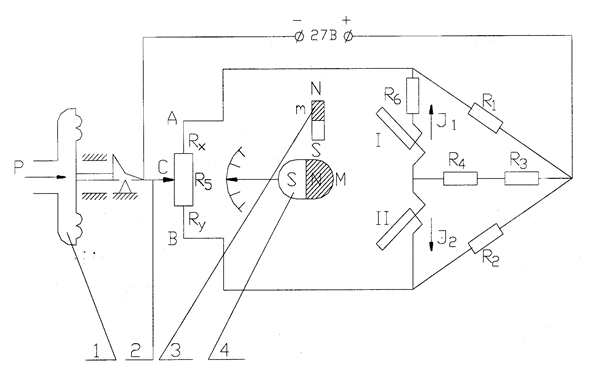
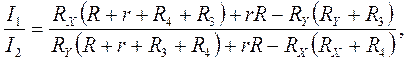 (1.7)
(1.7)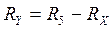 , в окончательном виде получим
, в окончательном виде получим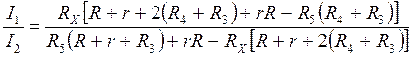 (1.8)
(1.8)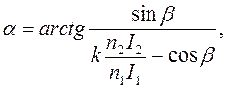 (1.9)
(1.9)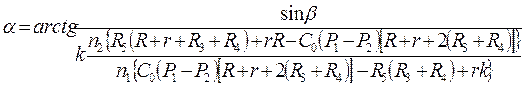 (1.10)
(1.10)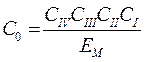 - обобщенный коэффициент.
- обобщенный коэффициент.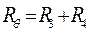 из условия независимости отношения токов от температуры окружающей среды q. Положим, что сопротивление рамки и полудиагонали R3 зависят от температуры окружающей среды:
из условия независимости отношения токов от температуры окружающей среды q. Положим, что сопротивление рамки и полудиагонали R3 зависят от температуры окружающей среды: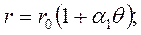
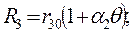
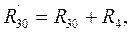 (1.11)
(1.11)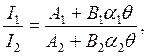 (1.12)
(1.12)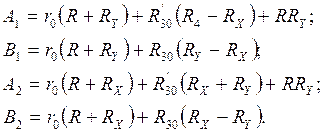
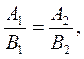 (1.13)
(1.13) не будет зависеть от окружающей температуры, т.е.
не будет зависеть от окружающей температуры, т.е. (1.14)
(1.14)


