
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення максимальної частоти процесуСодержание книги
Поиск на нашем сайте
Для вибору смуги пропускання частот приладу необхідно знати максимальну частоту вимірюваного процесу. Періодичну функцію x=x(t), що описує періодичний графік, можна представити у вигляді тригонометричного ряду Фур'є, що складається з постійної
де
Амплітуда
Постійна складова
У теорії рядів Фур'є доводиться, що зі збільшенням амплітуди гармоніки убувають до нуля. Отже, процес х(t) з деяким наближенням можна описати кінцевою сумою гармонік. Вважається, що процес досить точно описується такою сумою, коли остання обчислюється в сумі і гармоніка має амплітуду, приблизно в 10 разів меншу, ніж амплітуда першої, основної, гармоніки з частотою Таким чином, для визначення максімальної частоти періодичного процесу досить дослідити залежність амплітуд гармонік від частоти. Для прямокутного імпульсу, до якого за формою близькі графіки параметрів прокатки (див. рис. 1.1), залежність
де
На рисунку 1.6, а наведено графік залежності
Таким чином, максимальна частота процесу дорівнює частоті 10-й гармоніки,
а - періодичний; б – одиночний Рисунок 1.6. Спектри прямокутного імпульсу.
Якщо графік вимірюваної величини неперіодичний, то ряд Фур'є обертається в інтеграл Фур'є:
де
Тут S( Для прямокутного імпульсу спектральна щільність становить
На рисунку 1.6, б приведена залежність
Функція g(
Для процесів, що відрізняються за формою від прямокутного імпульсу, наприклад трапецеїдальної, косинусоїдальної форми, Для періодичного графіка (рис. 1.6, а) частотний інтервал між лініями, які зображують амплітуди гармонік, дорівнює основній частоті процесу Для невикревленого запису процесу х(t) з максимальною частотою необхідно, щоб прилад в діапазоні частот від нуля до
Таблиця 1.1 Максимальні частоти графиків моменту і тиску металу на валки.
При виборі смуги пропускання частот приладу іноді доводиться рахуватися з наступною обставиною. На вимірюваний процес можуть накладатися перешкоди з частотами, у кілька разів або десятків разів перевищують максимальну частоту процесу. Якщо частоти перешкод потрапляють в смугу пропускання частот приладу, то лінії запису виходять перекрученими (з щербинами). В цьому випадку бажано, щоб амплітудно-частотна характеристика приладу за межами частотного діапазону процесу різко спадала до осі частот. Тоді перешкоди надійдуть на вихід приладу ослабленими і запис вийде невикревленим. Така амплітудно-частотна характеристика виходить при застосуванні різних електричних фільтрів У таблиці 1.1 наведено максимальні частоти графіків моментів і тисків для деяких станів. Ці дані можна використовувати при виборі смуги пропускання частот апаратури.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 301; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.235.66 (0.009 с.) |

 і нескінченної суми гармонік:
і нескінченної суми гармонік: (1.14)
(1.14)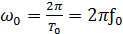 — кутова частота;
— кутова частота; та
та  — період і частота процесу.
— період і частота процесу. і фаза
і фаза 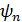 гармонік визначаються за формулами:
гармонік визначаються за формулами:
 (1.15)
(1.15) представляє собою середнє значення функції х(t) за період
представляє собою середнє значення функції х(t) за період  обчіслюється за формулою
обчіслюється за формулою (1.16)
(1.16) . Частоту останньої гармоніки називають максимальною частотою процесу.
. Частоту останньої гармоніки називають максимальною частотою процесу. від частоти
від частоти 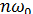 має вигляд:
має вигляд: (1.17)
(1.17) — амплітуда імпульсу;
— амплітуда імпульсу; — тривалість імпульсу;
— тривалість імпульсу; - період імпульсу.
- період імпульсу. при
при 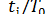 =1/3. На частотах, що задовольняють умові
=1/3. На частотах, що задовольняють умові  ,
,  приймає нульові значення, що означає, що гармоніки з номерами
приймає нульові значення, що означає, що гармоніки з номерами  відсутні. Амплітуди гармонік наступні:
відсутні. Амплітуди гармонік наступні: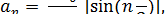
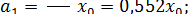







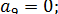
 (1.18)
(1.18) = 10
= 10  .
.
 (1.19)
(1.19)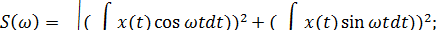
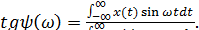 (1.20)
(1.20) ) має сенс «щільності», з якою на осі частот розподілені амплітуди гармонік, що становлять процес х(t). Тому S(
) має сенс «щільності», з якою на осі частот розподілені амплітуди гармонік, що становлять процес х(t). Тому S(  (1.21)
(1.21) (1.22)
(1.22) . Отже, максимальну частоту процесу виду одиночного прямокутного імпульсу тривалістю
. Отже, максимальну частоту процесу виду одиночного прямокутного імпульсу тривалістю 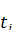 можна прийняти рівною
можна прийняти рівною  рад/сек або
рад/сек або (1.23)
(1.23) . Тому незалежно від форми графіка максимальну частоту процесу з деяким запасом можна визначати за формулою (1.23).
. Тому незалежно від форми графіка максимальну частоту процесу з деяким запасом можна визначати за формулою (1.23).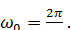 Такий спектр називається дискретним або лінійчатим. Одиночний графік можна розглядати як періодичний з періодом
Такий спектр називається дискретним або лінійчатим. Одиночний графік можна розглядати як періодичний з періодом  ; частотний інтервал між лініями нескінченно малий, тому такий спектр називається суцільним.
; частотний інтервал між лініями нескінченно малий, тому такий спектр називається суцільним. мав амплітудно- та фазо-частотну характеристики близькими до ідеальних. У ряді випадків досить допустити амплітудні викривлення в цьому діапазоні не більше 10%. При конструюванні приладу смугу пропускання частот передбачають ширше частотного діапазону вимірюваної величини, тому відпадає необхідність в обліку динамічних похибок через їх пренебрежимо малі величини.
мав амплітудно- та фазо-частотну характеристики близькими до ідеальних. У ряді випадків досить допустити амплітудні викривлення в цьому діапазоні не більше 10%. При конструюванні приладу смугу пропускання частот передбачають ширше частотного діапазону вимірюваної величини, тому відпадає необхідність в обліку динамічних похибок через їх пренебрежимо малі величини.



