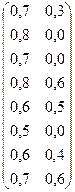Несколько замечаний по поводу конфирматорного ФА

Как было отмечено выше, конфирматорный ФА используется для проверки и подтверждения теоретической модели эмпирическими данными. Предполагается, что у исследователя есть достаточно строго сформулированная модель изучаемой им реальности (например, какие психологические факторы в межкультурном исследовании мотивации достижения у школьников являются общими для всех культур, а какие специфическим образом влияют на мотивационные переменные только в одной стране).

При использовании конфирматорного ФА исследователь (в рамках своей модели) четко формулирует гипотезу о числе общих и специфических факторов. Эта гипотеза должна основываться на серьезном анализе природы исследуемых переменных и лежащих в их основе факторов. Более того, проверяя свою модель на реальных данных, исследователь может делать и количественные предположения о величине корреляции между переменными, величинах факторных нагрузок для ряда исследуемых переменных и зависимости между факторами (ортогональными или косоугольными). Имея данные эмпирических измерений, с одной стороны, и набор разнообразных теоретических гипотез – с другой, психолог с помощью ФА фактически занимается проверкой сформулированных им гипотез о свойствах изучаемой (моделируемой) реальности. Для подробного знакомства с принципами конфирматорного ФА можно обратиться к книге П. Благуша «Факторный анализ с обобщениями». М. Финансы и статистика. 1989.

 

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПРИСТУПАЮЩИМ

К ПРАКТИЧЕСКОМУ ОСВОЕНИЮ ФАКТОРНОГО АНАЛИЗА

Основная трудность для начинающего – это, как ни странно, выбрать подходящий предмет для исследования, т.е. определить тот набор переменных, которые необходимо или интересно изучить с помощью ФА. При решении этой проблемы можно пойти двумя путями: либо взять заведомо подходящую задачу, которая ранее уже решалась с помощью ФА, либо придумать ее самому. Стандартный вариант – это провести ФА какого-либо известного опросника, в котором уже содержатся шкалы (факторы) и отражающие их вопросы (переменные). Еще лучше взять какой-либо новый (например, только что переведенный), но еще не стандартизированный опросник и провести исследование с ним. В этом случае будет интересно подумать над интерпретацией результатов ФА, и хотя бы немного побыть в роли разработчика новых психодиагностических методик. Неплохой вариант – найти в литературе данные, которые можно обработать ФА, и подумать над их интерпретацией в контексте обсуждаемых автором работы проблем.

Для ориентировки в том, что можно сделать, ниже приводится список названий работ по ФА, которые выполнялись в разное время студентами-психологами:

1. Оценка эмоционального состояния при прослушивании музыки разных жанров.

2. Личностные особенности деятелей тайных обществ первой трети XIX века.

3. Факторное пространство русских писателей XIX века.

4. Исследование факторов, определяющих положение человека в семье.

5. Изучение влияния различных типов стрессогенных ситуаций на интенсивность эмоционального переживания: определение специфики ситуаций для мужской и женской выборок.

6. Выделение скрытых факторов, обуславливающих привлекательность печатной рекламы.

7. Выявление факторов, оказывающих наибольшее влияние на выбор того или иного политического лидера при голосовании.

8. Факторы, способствующие заинтересованности человека той или иной пластинкой по виду ее конверта.

9. Характеристика человека, с которым мы хотим дружить.

10. Факторизация шкал опросника «16 PF».

11. Оценка изучаемых предметов студентами 2-го курса.

12. Выявление факторной структуры шкал акцентуации характера по Леонгарду (тест Шмишека). Сравнение результатов факторизации на 2-х выборках испытуемых.

13. Исследование факторов, влияющих на выбор страны для зарубежной поездки.

14. Факторы, определяющие оценку идеального мужчины и идеальной женщины.

15. Исследование факторов, определяющих специфику национального характера.

После того, как выбрана задача, которая будет решаться с помощью ФА, и в основном определен набор оцениваемых переменных, стоит еще раз подумать о правильности их выбора.

В первую очередь следует обратить внимание на то, чтобы переменные не повторяли друг друга, а разнообразно и всесторонне описывали предмет исследования. В разведочном исследовании тщательный подбор наблюдаемых переменных может обеспечить полноту описания изучаемой реальности. От этого и будет зависеть, сумеем ли мы выделить действительно важные факторы, влияющие на восприятие, оценку, понимание или действия человека в определенной ситуации, описываемой используемыми переменными. Например, если мы решили исследовать психологические факторы, которые определяют восприятие избирателями лидеров политических партий, то не следует ограничиваться оценкой только их личностных особенностей, безусловно стоит включить также и описательные характеристики их внешних данных, политических ориентации и многое другое.

Не следует забывать о том, что исследуемые факторы есть не более чем «экстракт» наблюдаемых переменных, и, следовательно, они не могут появиться из ничего. Однако не стоит и чрезмерно увеличивать число используемых переменных путем включения нескольких однотипных. Если несколько выбранных вами переменных похожи друг на друга, то очевидно, что это приведет к появлению очень высоких коэффициентов корреляции между этими переменными и, таким образом, к избыточности и односторонности описания предмета исследования.

В случае затруднения или сомнения в выборе необходимых переменных, полезно создать их заведомо избыточный список, а затем попросить коллег поучаствовать в его оценке в качестве экспертов.

Следующий важный этап в проведении исследования – сбор данных. Отметим только один – но очень важный – момент, касающийся этого этапа: какое количество наблюдений каждой переменной надо иметь? Ответ достаточно прост: чтобы получить статистически достоверные коэффициенты корреляции, нужно по каждой переменной собрать не менее 12-15 наблюдений. Если задача состоит в построении факторного пространства для одного испытуемого, то нужно решить, каким образом лучше получить от него такое количество повторных данных.

Ввод данных и их обработка. Остановимся кратко на некоторых важных этапах работы со статистической программой, с помощью которой собственно и реализуется процедура ФА, воспользовавшись в качестве одного из возможных примеров русскоязычной статистической системой «Stadia 6,0».

Работа в системе «Stadia». После вызова программы (stadia.ехе) вы сразу же попадаете в редактор данных и, следовательно, можете начинать ввод данных в электронную таблицу. Закончив ввод данных, не забудьте их сохранить на жестком диске – F4; практика показывает, что несоблюдение этого правила для неопытного пользователя часто заканчивается повторным вводом данных. Кроме того, обязательно проверьте правильность ввода данных (лучше эту малоприятную процедуру выполнять вдвоем: один читает – другой проверяет). В том случае, если данные уже набраны в каком-либо текстовом редакторе, вы можете загрузить их в окно редактора с дискеты, для чего используйте функцию «Чтение» – F3.

Войдя в меню статистических методов (F9), выберите в разделе «Многомерные методы» опцию «Факторный анализ». Первый запрос программы касается типа введенных данных – что это: матрица смешения (переменные объекты) или корреляционная матрица; как правило, вы начинаете работать с матрицей смешения. После расчета корреляционной матрицы появляется вопрос: «Записать ли рассчитанные корреляции в матрицу данных?»; чаще всего в этом нет особой необходимости. Далее на экране распечатывается таблица с показателями описательной статистики и матрица корреляций. Эта уже та информация, которую стоит записать в файл результатов – F2; в качестве имени файла (без расширения!) целесообразно ввести первые 6–8 букв своей фамилии. Если выводимая на экран информация не уместилась на одной экранной странице, нажмите клавишу «Enter». После этого на экране распечатается таблица с величинами собственных значений и процентом объясняемой дисперсии факторов (не забудьте сохранить и ее!) и появляется вопрос: «Выдать собственные векторы и новые координаты объектов?»; поскольку анализ собственных векторов используется редко, ответьте – «нет». А вот график собственных значений посмотреть весьма полезно, поэтому на следующий вопрос программы ответьте «да» и посмотрите его на экране. Затем производится расчет первичных факторных нагрузок и соответствующая матрица распечатывается на экране. Можно ее сохранить в файле и посмотреть факторные диаграммы, а можно ответить «нет» (чаще всего так и поступают) и, нажав «Enter», сразу перейти к вращению осей координат.

Для проведения вращения нужно обязательно указать число факторов, а затем выбрать метод вращения и ответить на вопрос «Нужна ли нормализация Кайзера?». Нормализация факторных нагрузок Кайзера выполняется для того, чтобы исключить влияние тех переменных, которые имеют по сравнению с другими переменными значительно большие значения нагрузок общих факторов.

После расчета факторных нагрузок производится расчет и распечатка коэффициентов общности и специфичности для каждого фактора и, конечно, матрицы факторных нагрузок после вращения. На этом этапе имеется возможность посмотреть факторную диаграмму переменных в осях «фактор 1 – фактор 2». После просмотра факторных диаграмм можно еще раз вернуться к выполнению процедуры вращения с новым (большим или меньшим) количеством факторов и опять проанализировать факторные диаграммы. После принятия решения о количестве факторов не забудьте сохранить в файле результатов соответствующую матрицу факторных нагрузок – F2. При необходимости любую факторную диаграмму можно распечатать на принтере или сохранить рисунок в виде файла.

ЛИТЕРАТУРА

Основная

1. Купер К. Индивидуальные различия. М., Аспект Пресс, 2000.

2. Наследов Д. А. Математические методы психологического исследования. Анализ и интерпретация данных. СПб., Речь, 2006.

3. Иберла К. Факторный анализ. М. Статистика. 1980

4. Ким Дж., Мьюллер Ч. Факторный анализ: статистические методы и практические вопросы / Ким Дж., Мьюллер Ч., Клекка У. и др. Факторный, дискриминантный и кластерный анализ. М. Финансы и статистика. 1989.

5. Мельников В. М., Ямпольский Л. Т. Введение в экспериментальную психологию личности. М., 1985.

Дополнительная

6. Благуш П. Факторный анализ с обобщениями. М. Финансы и статистика. 1989.

7. Гусев А.Н., Измайлов Ч.А., Михалевская М.Б. Измерение в психологии. М., 1997.

8. Кулаичев А. П. Методы и средства анализа данных в среде Windows. Stadia 6.0. М., 1999.

9. Митина О. В., Михайловская И. Б. Факторный анализ для психологов. М., 2001.

10. Петренко В. Ф. Основы психосемантики. СПб. Питер, 2005.

11. Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере. М., 1998.

 

ПРИЛОЖЕНИЕ

 

ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ВОПРОСОВ К ЗАЧЕТУ

1. Общая характеристика клинико-психологической систематизаций психологических знаний, двумерного и многомерного эксперимента в психологии.

2. Методы сбора данных в психологии личности (L, Q и T- данные).

3. Типологический подход к исследованию личности: обобщение данных путем группировки испытуемых.

4. Подход к исследованию личности, основанный на теории черт: обобщение данных путем группировки признаков.

5. Общая характеристика факторного анализа как научного метода

6. Матрицы: основные сведения о матрицах, виды матриц, чаще всего встречающиеся в факторном анализе.

7. Корреляционная и факторная матрицы: проблема факторов.

8. Корреляционная и факторная матрицы: проблема общности.

9. Геометрическая интерпретация одно- и двухфакторной матрицы.

10. Факторная матрица. Классификация факторов и связь между отдельными видами факторов

11. Используемые в факторном анализе важнейшие понятия, связанные с дисперсией

12. Проблема вращения в факторном анализе. Критерии простоты структуры

 

ЗАДАНИЯ ДЛЯ САМОПРОВЕРКИ

1. Предположим, что менеджер по персоналу провел факторный анализ оценок соискателей по ряду тестов. Как можно использовать этот анализ для того, чтобы решить, какие тесты больше не будут предсказывать, насколько хорошо работники справятся со своими обязанностями?

2. Почему получение «простой структуры путем вращения» всегда осуществляется в ходе факторного анализа?

3. Психолог изучает математические навыки в выборке, состоящей из 100 десятилетних детей. Это является частью ее дипломной работы. Она собрала данные по 120 заданиям теста, каждое из которых она оценивала как правильный или неправильный ответ. Она также учитывала место жительства каждого участника и намеревалась использовать факторный анализ ответов, чтобы заново выявить основную структуру математических способностей и установить, не выше ли математические способности детей в одних регионах по сравнению с другими. Какие советы можно ей дать?

4. Чему равны вклады общих факторов и характерного фактора в дисперсию Y₁:

Y₁=0.5f₁ + 0.8f₂ +0.33n₁ (f_1, f₂ и n₁ - общие и характерный факторы)

5. Найти общность и характерность параметра Y₁ если его надежность г² = 0,95, а специфичность b² = 0,15.

6. Заданы два общих фактора: a₁₁= 0,6; а₁₂= 0,5, а также надежность г² = 0,84. Составить полное уравнение для параметра Y₁.

7. Вычислить долю суммарной дисперсии, объясняемую каждым из двух общих факторов по заданной матрице А для восьми признаков (в матрице 8 строк), если вклад первого фактора в суммарную общность l₁=3.72, а вклад второго фактора в суммарную общность l₂=1,22

8. По заданной матрице А вычислить наибольшее и наименьшее значения характер­ности:

9. Постарайтесь приблизительно прикинуть, как корреляции между шестью заданиями теста, приведенные в таблице, будут выглядеть, если их представить в геометрическом выражении.

 

Таблица данных к заданию № 9

	Q1	Q2	Q3	Q4	Q5	Q6
Q1	1,000
Q2	0,933	1,000
Q3	0,824	0,696	1,000
Q4	-0,096	-0,052	0,000	1,000
Q5	-0,005	0,058	0,111	0,896	1,000
Q6	-0,167	-0,127	0,000	0,965	0,808	1.000

 

[1] На этом этапе очень важно определить достаточно большой набор характеристик, всесторонне описывающих измеряемый объект, и в то же время не содержащий лишних и несущественных. Именно продуманный и удачный подбор оцениваемых характеристик определяет в конечном счете успех в выделении существенных и значимых факторов – это основное, о чем нельзя забывать на данном этапе. С первого раза, априорно бывает трудно подобрать нужные характеристики. Поэтому надо помнить, что разведочное исследование с помощью ФА – это длительный процесс, когда результаты предыдущего анализа позволяют оценить допущенные ошибки и скорректировать процедуру последующего исследования.

 

[2] Существует тонкий вопрос, связанный с построением матрицы попарных корреляций: какую матрицу использовать в ФА – корреляционную или ковариационную? Рекомендации таковы: 1) если метрики переменных заметно отличаются (единицы измерения значительно неоднородны и дисперсии переменных заметно отличаются), то целесообразно использовать корреляционную матрицу; 2) ковариационные матрицы предпочтительнее, когда необходимо провести сравнение результатов ФА в двух различных выборках, полученных в одном и том же исследовании, например, когда требуется оценить повторяемость какого-либо интересного результата. Компьютерные программы ФА, как правило, задают пользователю вопрос, какую матрицу, корреляционную или ковариационную, он желает использовать.

 

 

[3] Более точно, собственные значения каждого фактора - это его вклад в дисперсию переменных, объясняемую влиянием общих факторов.

[4] Имеется в виду адекватность факторной модели данному набору переменных, описываемому корреляционной матрицей.

 

[Б1]

[Б2]