
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Индуктивность в электрической цепи.Содержание книги Поиск на нашем сайте Индуктивностью называется идеализированный элемент электрической цепи, приближающейся по свойствам к индуктивной катушке, в котором накапливается энергия магнитного поля.: Из закона сохранения энергии следует, что вся мощность, поступающая в цепь от источников энергии, в любой момент времени равна всей мощности, потребляемой приемниками данной цепи. То есть SPпотр. = SPист. Мощность потребителей, которыми в цепях постоянного тока являются резисторы, определяется по формуле Pпотр. = I2R Т.к. ток входит в данное выражение в квадрате, то независимо от его направления, мощность потребления всегда положительна. Мощность источников, бывает и положительной и отрицательной. Мощность источника э.д.с. определяется по формуле: Pэ.д.с. = EI Если э.д.с. и ток этой ветви совпадают по направлению, то мощность Pэ.д.с. входит в выражение баланса со знаком «+», если не совпадают – то Pэ.д.с. – отрицательная величина. Мощность источника тока определяется по формуле: Pи.т. = IU 11, Метод ктурных токов Метод контурных токов – один из основных и широко применяемых на практике методов. Он заключается в определении по второму закону Кирхгофа контурных токов. Для каждого контура цепи задают ток, который остается неизменным. В цепи протекает столько контурных токов, сколько независимых контуров в ней содержится. Направление контурного тока выбирают произвольно. Контурные токи, проходя через узел, остаются непрерывными. Следовательно, первый закон Кирхгофа выполняется автоматически. Уравнения с контурными токами записываются только для второго закона Кирхгофа. Число уравнений, составленных по методу контурных токов, меньше чем по методу законов Кирхгофа. На рис показана цепь с двумя независимыми контурами, следовательно, и с двумя контурными токами I11 и I22. Токи в ветвях I1 и I2 равны контурным токам:I1=I11, I2=I22,I3=I11+I22 По второму закону Кирхгофа для первого контура цепи: I1r1+I3r3=E1-E3 Или: I11r1+(I11+I22)r3=E1-E3; I11 (r1+r3)+I22r3=E1-E3 Обозначим r1+r3=r11 r3=r12; E11=E1-E3 Тогда: I11r11+I2r12=E11 r11 – сумма всех сопротивлений, входящих в контур I, называется собственным сопротивлением контура. r12 – сопротивление ветви, общей для контура I и II;E11=E1-E2 – алгебраическая сумма всех э.д.с., содержащихся в первом контуре; со знаком «-» берется э.д.с., действующая навстречу контурному току рассматриваемого контура. E11 называется контурной э.д.с. Аналогично для второго контура рис.1. I11r21+I22r22=E22, где r21=r3; r22=r2+r3; E22=E2-E3 Уравнения, составленные по методу контурных токов, всегда записывают в виде системы.
Число уравнений, составляемых по методу контурных токов, определяется по формуле: Nур=Nb-Ny+1-Nи.т. где Nb – число ветвей электрической цепи; Ny – число узлов;Nи.т. – число идеальных источников тока.
Т.е., под эквивалентностью треугольника и звезды понимается то, что при одинаковых напряжениях между одноименными зажимами токи, входящие в одноименные выводы, одинаковы. Сопротивление луча звезды равно произведению сопротивлений сторон треугольника, прилегающих к этому лучу, деленному на сумму сопротивлений трех сторон треугольника. При переходе от звезды к треугольнику известными являются сопротивления R1, R2, R3 лучей звезды. Значения сопротивлений треугольника определяются в результате совместного решения уравнений
Сопротивление стороны треугольника равно сумме сопротивлений прилегающих лучей звезды и произведения их, деленного на сопротивление третьего луча. Преобразование звезды в эквивалентный треугольник. При переходе от звезды к треугольнику известными являются сопротивления R1, R2, R3 лучей звезды. Значения сопротивлений треугольника определяются в результате совместного решения уравнений: Ток в любой ветви «a-b» линейной электрической цепи не изменится, если электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным источником тока. Ток этого источника должен быть равен току между зажимами a-b закороченными накоротко, а внутренняя проводимость источника тока должна равняться входной проводимости пассивной электрической цепи со стороны зажимов «a» и «b» при разомкнутой ветви «ab».
20, Метод эквивалентного генератора. Методы решения задач, основанные на теоремах об эквивалентном источнике напряжения и об эквивалентном источнике тока, называются соответственно методом эквивалентного генератора и методом эквивалентного источника тока. Эти методы используются в тех случаях, когда по условию задачи требуется рассчитать ток только одной ветви электрической цепи. Порядок расчета задачи методом эквивалентного генератора: **разрывают выделенную ветвь схемы и путем расчета оставшейся части схемы одним из методов определяют Uxx на зажимах разомкнутой ветви; **определяют r0 (внутренне сопротивление эквивалентного источника) по отношению к зажимам выделенной ветви методом эквивалентных преобразований. **При этом обязательно изображается пассивная схема, где источники э.д.с. заменяются их внутренними сопротивлениями (если э.д.с. - идеальная, то участок ее подключения изображается короткозамкнутым), источники тока заменяются их внутренними проводимостями (ветви с идеальными источниками тока разрываются); **Определяют ток выделенной ветви по закону Ома:
21. Основные понятия о переменном синусоидальном токе. Электрический ток и напряжение изменяющиеся во времени по какому-либо закону называют переменными. Если форма кривой переменного тока и напряжения повторяется через равные промежутки времени, то их называют периодическими. Наименьшее время, через которое повторяется форма переменного тока и напряжения, называют периодом Т и измеряют в с. Число периодов Т в 1 секунду называют частотой f переменного тока и напряжения и дана размерность герц (Гц). f=1/T Простейшими периодическими переменными током и напряжением являются вырабатываемые генераторами всех видов электростанций напряжения и тока (энергия) синусоидальной формы.
22, Действующие и средние периодич ЭДС и токи Периодические ток и напряжение характеризуют еще понятиями среднего и действующего значения. Среднее значение – это среднее значение за период. Так как у синусоидальной функции оно равно нулю, у синусоидального тока и напряжения за среднее значение определяют значение за полпериода . Действующее значение периодической синусоидальной функции – это среднеквадратичное значение за период.
23, Мощность в цепи переменного синусоид тока.
U×I=S – полная мощность; U×I×Cos j=P – активная мощность; U×I×Sin j=Q – реактивная мощность.
|
|||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.006 с.) |




 13, Преобразованием треугольника в эквивалентную звезду называется такая замена части цепи, соединенной по схеме треугольником, цепью, соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи сохраняются неизменными.
13, Преобразованием треугольника в эквивалентную звезду называется такая замена части цепи, соединенной по схеме треугольником, цепью, соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи сохраняются неизменными.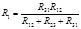
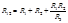

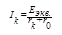 .
.

 или Iср=0,64 Im, Uср=0,64 Um.
или Iср=0,64 Im, Uср=0,64 Um.
 , B Разница между амплитудным и действующим значением периодического синусоидального тока и напряжения
, B Разница между амплитудным и действующим значением периодического синусоидального тока и напряжения  .По действующему значению I периодического синусоидального тока судят о его тепловом воздействии.
.По действующему значению I периодического синусоидального тока судят о его тепловом воздействии.
 Здесь:
Здесь:


