Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные характеристики датчиковСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ВВЕДЕНИЕ Проблемы автоматизации производственных процессов и мониторинга состояния окружающей среды успешно решаются при наличии датчиков соответствующих величин. В основе работы большинства современных твердотельных датчиков используется несколько фундаментальных эффектов воздействия на полупроводниковые сенсоры таких параметров, как деформация, температура, магнитное поле, окружающая газовая среда, оптическое облучение и др. Учебное пособие «Введение в сенсорику» посвящено описанию физических принципов работы, конструкции, основных параметров и технологии изготовления наиболее распространенных датчиков физических величин. В датчиках других величин, не описанных в учебном пособии, в качестве чувствительных элементов часто используются рассмотренные в пособии сенсоры деформации, температуры, магнитного поля. Например, терморезисторы являются чувствительными элементами датчиков скоростей газовых и жидкостных потоков (термоанемометров), датчиков – газоанализаторов, датчиков вакуума; тензорезисторы – чувствительные элементы датчиков сил, ускорений, давлений; холловские датчики используются для измерения положения и перемещения. Полупроводниковые датчики в большинстве случаев отличаются сравнительно простой технологией изготовления и не требуют сложного технологического оборудования, поэтому могут производиться не только на крупных промышленных предприятиях, но и в условиях мелкосерийного производства. ОБЩИЕ СВЕДЕНИЯ О ДАТЧИКАХ ФИЗИЧЕСКИХ ВЕЛИЧИН Основные характеристики датчиков
Датчиками называются устройства, которые под воздействием физической измеряемой величины выдают эквивалентный сигнал, обычно электрической природы, являющийся функцией измеряемой величины:
S = F(m), (1.1)
где S – выходная величина датчика; m – входная величина. Соотношение (1.1) выражает в общей теоретической форме физический закон, лежащей в основе работы датчика. Этот закон, выраженный численно, определяет выбор конструкции и материала для его изготовления, допустимые характеристики окружающей среды и условия его применения. Для удобства измерений датчик стараются построить так, чтобы существовала линейная связь между малыми приращениями выходной ΔS и входной Δm величин:
ΔS = γ Δm, (1.2)
где γ – чувствительность датчика. Постоянство чувствительности является важной проблемой создания датчиков. Диапазон измеряемых значений – динамический диапазон внешних воздействий (максимальный входной сигнал), которые датчик может преобразовать в электрический сигнал, не выходя за пределы допустимых погрешностей. Диапазон выходных значений – разность между электрическими выходными сигналами, измеренными при максимальном и минимальном внешнем воздействии. Погрешность измерений датчика – разность между значением, вычисленным по выходному сигналу, и реальным значением входного сигнала. Погрешность датчика определяет его точность. Она может быть представлена в виде: непосредственно в единицах измеряемой величины (абсолютная погрешность); в процентах от значения максимального входного сигнала; в единицах выходного сигнала. Мертвая зона – это нечувствительность датчика в определенном диапазоне входных сигналов. В пределах этой зоны выходной сигнал остается почти постоянным (равным нулю). Разрешающая способность – это минимальное изменение входной величины, которое может почувствовать датчик. Быстродействие датчика удобно оценивать постоянной времени – временем инерционности датчика. Это время, в течение которого выходной сигнал датчика достигнет уровня, составляющего 63 % от установившегося значения, после подачи на вход внешнего воздействия, т.е. изменится в е раз.
Классификация датчиков Существуют различные классификации датчиков: по назначению, области применения, конструктивно-техническим особенностям, техническим характеристикам и др. Наиболее широко применяемым принципом преобразования физических величин является преобразование их в изменение сопротивления чувствительного элемента, реализуемое в резисторных датчиках (тензо-, термо-, фото-, магниторезисторах). Емкостные датчики в простейшем случае состоят из двух электродов, разделенных малым воздушным зазором. Изменение зазора или перекрывающихся площадей электродов, а также заполнение воздушного зазора другим веществом вызывают изменение емкости. Пьезоэлектрические датчики основаны на прямом и обратном пьезоэффекте (поляризации вещества под действием механических напряжений и деформации его в электрическом поле). Разновидностью таких датчиков являются датчики на основе пьезорезонаторов. Частота резонансных колебаний в пьезоэлементе зависит от многих физических параметров, на этом основан их принцип работы.
ДАТЧИКИ ДЕФОРМАЦИИ Принцип действия В основе работы большинства датчиков деформации лежит тензорезистивный эффект – изменение электрического сопротивления датчика при его деформировании. Такие датчики называются тензорезисторами. Электрическое сопротивление твердого тела изменяется при деформации как за счет изменения геометрических размеров, так и за счет изменения удельного сопротивления материала. В случае одноосного напряжения (например, при растяжении) относительное изменение сопротивления dR/R элемента длиной l с удельным сопротивлением ρ и коэффициентом Пуассона νп равно
dR/R = (1 + 2 νп) dl/l + dρ/ρ. (2.1)
В уравнении (2.1) первое слагаемое определяет изменение геометрии тела, второе – изменение удельного сопротивления. Так как ν Приращение сопротивления за счет изменения удельного сопротивления зависит от структуры и свойств материала и может быть в десятки и сотни раз больше, чем за счет геометрии. Принято обозначать – изменения взаимодействия между электронами и упругими волнами в кристалле, приводящего к изменению подвижности электронов; – изменения энергии Ферми, приводящего к изменению числа электронов проводимости; – изменения зонной структуры вследствие перекрытия, сближения или удаления различных зон; – возникновения новых кристаллических модификаций. У большинства металлических материалов (металлов и сплавов) изменение удельного сопротивления в основном обусловлено изменением подвижности электронов при деформации. Приращения сопротивления металлов и сплавов в области упругой деформации изменяются линейно. Поэтому уравнение (2.1) можно записать в виде
где
называется коэффициентом тензочувствительности. Для большинства металлов и сплавов в области упругой деформации В полупроводниковых материалах коэффициент тензочувствительности принимает значения от (–100) до +200, что в значительной степени определяется большой величиной коэффициента m. Тензочувствительность в полупроводниках зависит от кристаллографического направления, типа проводимости и удельного сопротивления, с ростом которого тензочувствительность растет, рис. 2.1.
Рис. 2.1. Зависимость тензочувствительности кремния
от удельного сопротивления при различном типе проводимости и в различных кристаллографических направлениях: 1 – p -тип, [111]; 2 – р -тип, [110]; 3 – р -тип, [100]; 4 – n -тип, [111]; 5 – n -тип, [110]; 6 – n -тип, [100]
Причиной изменения удельного сопротивления полупроводника при деформации может быть либо изменение концентрации носителей заряда, либо изменение их подвижности. Для
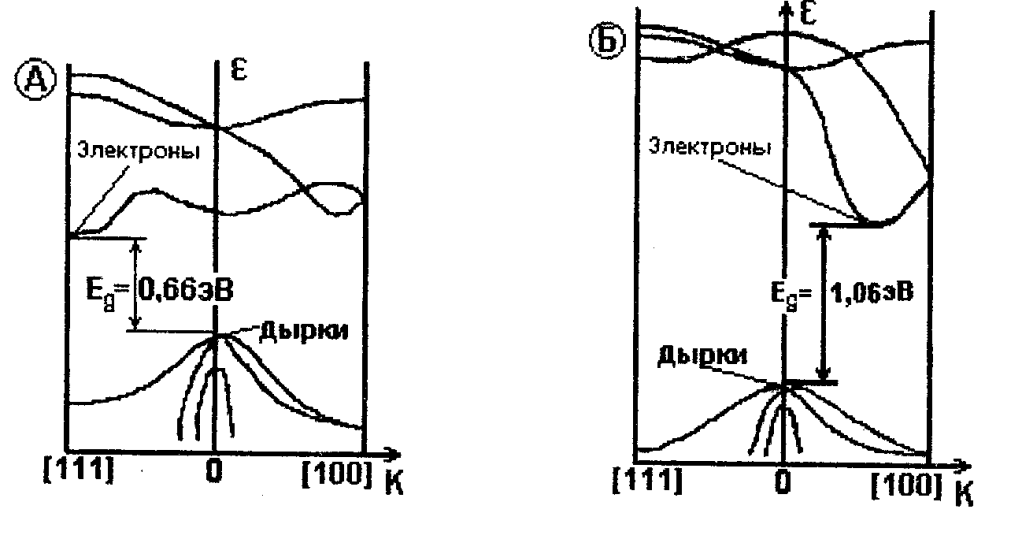
где n – концентрация электронов, μ n – их подвижность. При деформации может изменяться либо концентрация, либо подвижность, либо одновременно оба этих параметра. В полупроводниках изменение концентрации носителей заряда при деформации может быть вызвано изменением ширины запрещенной зоны и энергии ионизации примеси, а также изменениями эффективных плотностей состояний в валентной зоне и зоне проводимости. Однако помимо влияния деформации на концентрацию носителей заряда сильно влияет температура, поэтому при ее изменении тензорезистор будет показывать «кажущуюся» деформацию. С целью уменьшения влияния температуры на работу тензорезисторов для их изготовления используются сильнолегированные полупроводники, температурный рабочий диапазон которых приходится на участок истощения примесной проводимости (на котором концентрация носителей заряда равна концентрации легирующей примеси, она остается постоянной как при изменении деформации, так и при изменении температуры). Поэтому рассмотрим вторую причину изменения удельного сопротивления при деформации – изменение подвижности, являющуюся основной при объяснении тензоэффекта в полупроводниках. Высокая тензочувствительность связана со сложной структурой энергетических зон полупроводников, причем тензоэффект в полупроводниках разного типа проводимости имеет различную природу и связан с перераспределением носителей заряда между различными подзонами. Рассмотрим Si и Ge n-типа проводимости, энергетическая структура которых приведена на рис. 2.2. Зависимость энергии от волнового вектора Е(k) в зоне проводимости имеет несколько минимумов энергии. Соответствующие минимумам изоэнергетические поверхности в k-пространстве являются эллипсоидами вращения, вытянутыми вдоль осей симметрии кристалла. В Si это направления [100], поэтому имеется 6 эквивалентных долин для электронов, в Ge - направления [111], имеются 4 эквивалентные долины. Ввиду несферичности изоэнергетических поверхностей вводятся две эффективные массы для электронов: в продольном
,. Рис. 2.2. Энергетическая структура германия (А) и кремния (Б)
В недеформированных кристаллах все долины эквивалентны и концентрация электронов в них одинакова. При приложении одноосной деформации эквивалентность долин может нарушаться, что приведет к перераспределению электронов между ними. Долины, дно которых опустится, дадут больший вклад в проводимость, чем те долины, дно которых поднимется. В условиях анизотропии подвижностей электронов это ведет к изменению проводимости. Например, если сжать кристалл Si вдоль оси [100], то расстояния между атомами в этом направлении уменьшатся, обменный интеграл для этого направления возрастет, а для направлений [010] и [001] уменьшится. Это приведет к тому, что дно зоны проводимости в [100] опустится, а в перпендикулярных направлениях – поднимется, концентрация электронов в [100] возрастет, а в перпендикулярных направлениях уменьшится при сохранении суммарной концентрации во всех долинах. Рассмотрим перераспределение электронов только между двумя минимумами – в [100] и [010]. При отсутствии деформации электропроводность этих двух минимумов
где n1 = n2 = n0/2 – от направления не зависит; n0 – суммарная концентрация электронов; μ0 = При сжатии в [100] n1 увеличивается, а n2 –уменьшаетcя на Δn. Электропроводность при сжатии
σД -= e [(n1 + Δn)
Так как
определяется количеством перераспределенных электронов и отношением подвижностей α = При сжатии вдоль [111] деформация вдоль осей <100> одинакова, минимумы смещаются в одном и том же направлении на одну и ту же величину, нет переходов электронов из долины в долину, нет и изменения проводимости. Аналогично можно определить изменение электропроводности при деформации с учетом всех минимумов. Максимальное изменение подвижности происходит при деформации в направлении расположения нижних минимумов: в n-Gе в направлении [111], в n -Si в направлении [100]. В Gе, Si и GаАs р-типа проводимости анизотропии подвижности дырок практически нет. Как видно из рис. 2.1, в вершине валентной зоны соприкасаются две ветви энергии, т.е. вершина валентной зоны является вырожденной. Этим ветвям соответствуют различные эффективные массы дырок, в связи с чем подзону с малой эффективной массой называют подзоной "«легких"» дырок, а большой – «тяжелых». При одноосной деформации нарушается симметрия кристалла, что приводит к снятию вырождения, т.е. подзоны легких и тяжелых дырок смещаются в противоположных направлениях. Это приводит к перераспределению дырок между подзонами. Если
где
так как общая концентрация дырок Относительное изменение проводимости
Максимальное изменение подвижности дырок Gе, Si и GаАs р -типа проводимости происходит при деформации в направлении [111]. В Gе п- и р-типа проводимости наибольшая тензочувст-вительность наблюдается в направлении [111], в Si n -типа в направлении [100] и в Si р -типа в направлении [111]. Знак тензочувствительности в полупроводниках n -типа отрицательный, а в полупроводниках р -типа – положительный. Наибольшее значение коэффициента тензочувствительности для Gе и Si порядка 150 – 170. Тензочувствительность GаАs р -типа максимальна в направлении [111] и достигает такой же величины, как в Gе и Si. Большой тензочувствительностью обладают соединения n -GаSb в направлении [111] ( . ДАТЧИКИ ТЕМПЕРАТУРЫ Из большого количества методов измерения температуры (оптических, механических, магнитных и др.) наиболее простыми и широко используемыми являются электрические методы, а в качестве датчиков температуры чаще всего используются терморезисторы и термопары.
Принцип действия Термопары Принцип работы термопары основан на эффекте Зеебека: если составить цепь из двух различных проводников (или полупроводников) А и В, соединив их между собой, и температуру Т1 одного места соединения (спая) сделать отличной от температуры Т2 другого, то в цепи потечет ток под действием эдс, называемой термоэлектродвижущей силой (термоэдс), зависящей от материалов проводников А и В и от разности температур Т1 и Т2. При небольшом перепаде температур между спаями термоэдс пропорциональна разности температур ЕАВ = SАВ ΔТ. Термоэлектрический контур можно разомкнуть в любом месте и включить в него один или несколько разнородных проводников. Если места этих соединений находятся при одной температуре, то не возникает паразитных термоэдс. Поэтому прибор для измерения термоэдс может быть включен как между свободными концами термопары, так и в разрыв одного из термоэлектродов. Обычно температура одного спая постоянна и известна, она служит опорной (нулевой) точкой Т1 = Т0. Температура другого спая Т2 является температурой ТС, которую приобретает спай в исследуемой среде с температурой ТХ. Температура ТС зависит от ТХ и тепловых потоков, которые устанавливаются между спаем и окружающей средой. Так как размеры спая могут быть очень малыми, измерение термопарой обеспечивает высокое быстродействие и возможность точечных измерений температуры. В этом преимущества термопар в сравнении с термометрами сопротивлений. Другое достоинство термопары – вырабатываемый сигнал (эдс), для его измерения не нужно пропускать ток через датчик, поэтому нет саморазогрева, что важно в системах с малой тепловой инерцией или при низких температурах. В широком диапазоне температур термоэдс является нелинейной функцией ТС. Термопары в зависимости от их типа применимы от очень низких температур (–270 ºС для термопары медь – сплав серебра с кобальтом) до очень высоких (2700 ºС для термопары вольфрам- рений 5 % – вольфрам-рений 26 %). Эти температуры на 1400 ºС выше максимальной рабочей температуры термометров сопротивления. Чувствительность SAB термопары к температуре при ТС определяется соотношением SAB(ТС) = dEAB/dTC, зависит от температуры и выражается в микровольтах на градус Цельсия. Для термопары железо – константан S(0 ºС) = 52,9 мкВ/ºС, S(700 ºС) = 63,8 мкВ/ºС; для термопары платинородий - платина S (0 ºС) = 6,4 мкВ/ºС, S (1400 ºС) = 11,93 мкВ/ ºС. Сравнивая эти значения с чувствительностью измерительных установок с термометрами сопротивления, следует вывод, что термопары имеют низкую чувствительность. Термисторы Термистор – это полупроводниковый терморезистор с отрицательным ТКС. Они имеют чувствительность к температуре примерно в 10 раз большую, чем металлические. Отрицательный ТКС может быть вызван разными причинами: увеличением концентрации или подвижности носителей заряда с ростом температуры, а также фазовыми превращениями материала. Первое явление характерно для термисторов из монокристаллов ковалентных полупроводников (Si, Ge, SiC, соединений типа А3В5 и др.). Они имеют отрицательный ТКС для температур, соответствующих участкам примесной и собственной проводимости. Зависимость сопротивления определяется в основном изменением концентрации носителей заряда, температурным изменением подвижности можно пренебречь. Для этих диапазонов характерна температурная зависимость сопротивления
R = R0 exp(B/T), (3.5)
где В – коэффициент температурной чувствительности; R0 – постоянная, зависящая от материала и размеров термистора; Т – температура, К. При неполной ионизации примесей и отсутствии компенсации В = ΔЕ/2k, где ΔЕ – энергия ионизации примеси, k – постоянная Больцмана. Для компенсированного полупроводника при неполной ионизации примеси В = ΔЕ/k. Для участка собственной проводимости В = Еg/2k, где Еg – ширина запрещенной зоны полупроводника. Вторая причина изменения сопротивления характерна для термисторов из поликристаллических окисных полупроводников – из окислов металлов переходной группы таблицы Менделеева (от титана до цинка). Металлы этой группы имеют переменную валентность и незаполненные электронные оболочки. Электропроводность таких материалов связана с обменом электронами между соседними ионами. Энергия такого обмена мала, поэтому все электроны (или дырки) можно считать свободными, а их концентрацию – постоянной. Подвижность носителей заряда в таком полупроводнике мала, она экспоненциально возрастает с повышением температуры. В результате температурная зависимость сопротивления окисного полупроводника оказывается такой же, как у ковалентного, а коэффициент температурной чувствительности характеризует изменение подвижности носителей заряда, а не изменение их концентрации. В окислах ванадия VO2, V2O3 при температуре фазовых превращений (68 и –110 ºС) наблюдается уменьшение сопротивления на несколько порядков. Это явление используется для изготовления термисторов с большим отрицательным ТКС при температурах фазовых превращений. Сравним чувствительность к температуре металлических терморезисторов и термисторов с чувствительностью термопар. Для этого включим терморезистор в одно плечо моста Уитстона, а в три другие – постоянные сопротивления с R = R0, где R0 – начальное значение сопротивления терморезистора. Напряжение разбаланса моста равно
U =
где ЕП – напряжение питания моста; Для платины
Позисторы Позисторы – это полупроводниковые терморезисторы с положительным ТКС. В массовом производстве позисторы делают из титанато-бариевой керамики, сопротивление которой снижено добавлением примесей. BaTiO3 – диэлектрик с ρ = 1010 – 1012 Ом·см при комнатной температуре. Примеси от 0,1 до 0,3 ат.% редкоземельных элементов (лантана, церия и др.) уменьшают удельное сопротивление до 10 – 100 Ом·см. При температуре точки Кюри титанат бария переходит из сегнетоэлектрического в параэлектрическое состояние. Такой материал обладает аномальной температурной зависимостью сопротивления: в узком диапазоне температур с ростом температуры сопротивление увеличивается на несколько порядков. Для смещения точки Кюри в сторону низких температур используются твердые растворы BaTiO 3 – SrTiO3 и BaTiO3 – BaSnO3 (увеличивают относительное содержание Sr и Sn в керамике). Диапазон рабочих температур позисторов на основе BaTiO3 65 – 150 ºС, ТКС достигает (0,1 – 0,5) К-1. Для создания позисторов используются и монокристаллические Si, Ge и другие полупроводники. Принцип действия этих позисторов основан на уменьшении подвижности носителей заряда с увеличением температуры вследствие усиления их рассеивания на фононах. При этом концентрация носителей заряда остается постоянной, так как используется участок истощения примесной проводимости. Кремниевые термометры сопротивления с малой концентрацией примеси (1015 – 1017 см-3) имеют ТКС (0,7 – 1)·10-2 К-1, диапазон рабочих температур от –50 до 120 ºС. ТКС таких позисторов тем выше, чем меньше концентрация примеси.
И транзисторов
Термодиоды и термотранзисторы находят применение в датчиках температуры, работающих в диапазоне от –80 до +150 ºС. Верхняя граница температурного диапазона ограничивается тепловым пробоем p-n перехода и для некоторых кремниевых датчиков достигает 500 ºС. Нижняя граница температурного диапазона определяется уменьшением концентрации основных носителей и может достигать для датчиков из Ge – (240 – 260) ºС, из Si – (–200 ºС). Связь между током I через p-n переход и падением напряжения U на нем определяется уравнением
I = I0e-B/T(eqU/(kT) – 1), (3.7)
где I0e-B/T = Iнас – ток насыщения, зависящий от температуры Т; I0 – ток насыщения при Т → ∞; q – заряд электрона; k – постоянная Больцмана. Это уравнение определяет ток через p-n переход как при прямом, так и при обратном смещении. Учитывая, что при Т = 300 К kT/q = 26 мВ, при напряжениях на переходе
Iпр = I0 e-B/T eqU/(kT), Iобр = I0e-B/T. (3.8)
Прямой и обратный токи являются функциями температуры, однако для измерения температуры чаще используются открытые p-n переходы. Падение напряжения на открытом переходе при токе I через переход определяется формулой
U = [kT ln(I/I0) + kB]/q, (3.9)
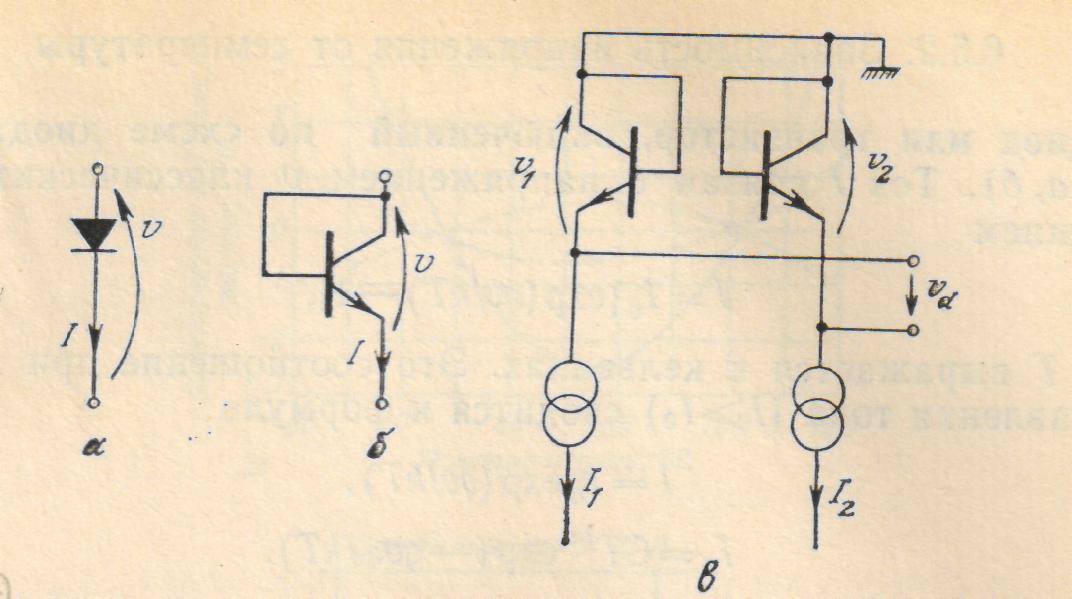
из которой видно, что U линейно зависит от Т и уменьшается с увеличением температуры (I0 >> I). Температурная чувствительность p-n перехода по напряжению составляет 1,5 – 2,5 мВ/К. Сравнивая эту величину с чувствительностью термопар, видно, что p-n переходы в 100 раз чувствительнее термопар. Используемые для измерения температуры элементы – диоды и транзисторы, включенные по схеме диода (коллектор замкнут на базу), питаются постоянным током I в прямом направлении, напряжение U на выводах, зависящее от температуры, является выходной электрической величиной датчиков, изображенных на рис. 3.1. Микроэлектронная технология дает возможность изготовить оба транзистора датчика, изображенного на рис. 3.1,в, в виде интегральной схемы на одном кристалле.
Термопары Диапазон температур, в котором применима термопара, ограничиваются при низких температурах снижением термоэлектрической способности, а при высоких – опасностью проникновения примесей из внешней среды, испарением одного из компонентов сплава термопары, рекристаллизацией, плавлением и др. В табл. 3.1 указаны рабочие диапазоны температур для термопар основных типов и точность стандартных термопар. Максимальная рабочая температура будет тем ниже, чем тоньше проволока. У термопар типов B, R, S проволока должна быть изолирована от металлического корпуса слоем окиси алюминия для предотвращения диффузии паров металла оболочки в проводники термопары. Если термопара облучается потоком нейтронов, нельзя применять металлы, в которых могут произойти ядерные превращения, например, родий и медь; железо и никель в этих условиях стабильны.
а б в
Рис. 3.1. Элементы, используемые в качестве датчиков температуры: а – диод; б – транзистор, включенный по схеме диода; в – пара транзисторов, включенных по схеме диода
Спай термопары должен иметь малый объем, чтобы не было неравномерностей температуры в различных точках. Чтобы избежать контакта за пределами измерительных спаев, проволока пропускается через керамические изоляторы, которые должны быть химически инертными и иметь большое сопротивление при высокой температуре. Таблица 3.1
Основные типы термопар и их технические характеристики
Отечественной промышленностью выпускаются следующие типы термопар: хромель – копель, тип ТХК; хромель – алюмель, тип ТХА; платинородий (10 %) – платина, тип ТПП; платинородий (30 %) – платинородий (6 %), тип ТПР; вольфрам-рений (5 %) – вольфрам-рений (20 %), тип ТВР. Градуировочные таблицы для этих термопар приведены в ГОСТ Р 8.585 – 2001. Рабочий спай термопары может быть открытым или закрытым (защищенным от окружающей среды), что увеличивает тепловую инерционность термопары. Тепловая инерционность термопары определяется постоянной времени, для этого она погружается в воду с температурой, отличной от температуры окружающей среды. Постоянная времени – это время, в течение которого температура термопары изменится на 63 % (в е раз). Постоянная времени промышленных термопар составляет от 5 до 180 с. Значительно снизить постоянную времени позволяют тонкопленочные термопары, полученные соединением двух пленок разных металлов. Такие термопары бывают двух типов типов: в виде пленок на съемном носителе и в виде матрицы с датчиком, встроенным в тонкий многослойный материал. Толщина металлической фольги, используемой в таких термопарах, составляет около 5 мкм, это объясняет малое значение постоянной времени таких термопар – 10 мс.
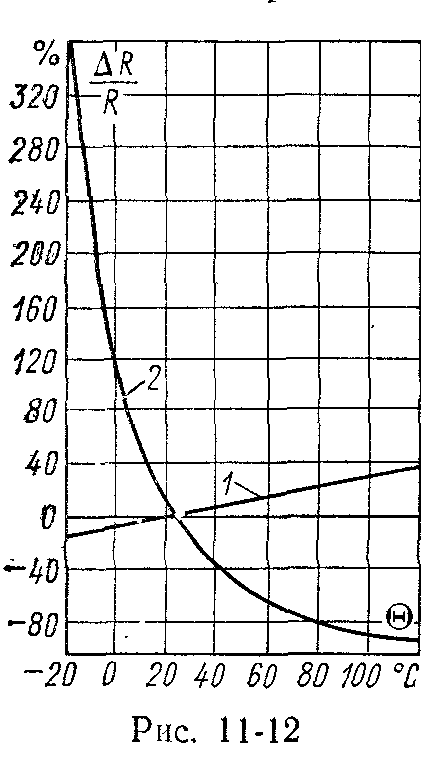
Термисторы Термисторы, выпускаемые промышленностью, в основном изготовлены из поликристаллических оксидных полупроводников методами керамической технологии. Такие термисторы могут быть изготовлены и различными методами пленочной технологии. Конструктивно термисторы могут иметь разнообразные формы: дисковые, бусинковые, стержневые, каплевидные. Термисторы ММТ-1 и КМТ-1 представляют собой полупроводниковый стержень, покрытый эмалевой краской, с контактными колпачками и выводами; используется в сухих помещениях. Термисторы ММТ-4а и КМТ-4а заключены в металлические капсулы и герметизированы, а термисторы СТ1-19, СТ3-19 имеют каплевидную форму и оплавлены стеклом. Температурная характеристика термистора – это зависимость его сопротивления от температуры – рис. 3.2.
Рис. 3.2. Температурная зависимость сопротивления медного терморезистора (1) и термистора (2)
Номинальное сопротивление термистора Rном – сопротивление при определенной температуре (обычно при 20 ºС). Термисторы изготавливают с допустимыми отклонениями от Rном ±20, 10 и 5 %. Коэффициент температурной чувствительности В – коэффициент в показателе экспоненты температурной характеристики термистора в формуле (3.5). Значение В зависит от свойств материала термистора и практически постоянно для данного термистора в рабочем диапазоне температур. В находится в пределах от 700 до 15·103 К. ТКС термисторов (относительное изменении сопротивления термистора при изменении температуры на один градус) определятся так же, как для металлических термометров сопротивления по формуле (3.2). ТКС термистора зависит от температуры, поэтому его записывают с индексом, указывающем температуру. Зависимость ТКС от температуры можно получить из уравнений (3.2) и (3.5): αR = –B/T2. Значения ТКС для термисторов находятся в пределах (0,8÷8)∙10-2 К-1. Коэффициент рассеяния термистора Н равен мощности, рассеиваемой термистором при разности температур термистора и окружающей среды в 1 ºС. Максимально допустимая температура – это температура, при которой не происходит необратимых изменений параметров и характеристик термистора. Она зависит не только от свойств материала термистора, но и от его конструктивных особенностей. Минимальная мощность рассеяния Рmin (или коэффициент энергетической чувствительности) – это мощность, при которой у термистора, находящегося в спокойном воздухе при температуре (20 ± 1) ºС, сопротивление уменьшается от разогрева током не более, чем на 1 %. Максимальная мощность рассеяния Рmax – это мощность, при которой термистор, находящийся при тех же условиях, разогревается током до максимально допустимой температуры. Допустимая мощность рассеяния Рдоп – это максимальная мощность при максимально допустимой температуре. Мощность Pmin связана с коэффициентом рассеяния Н и ТКС αR cоотношением Pmin = Н/αR. Постоянная времени τ – это время, в течение которого температура термистора изменится в е раз (на 63 %) при переносе термистора из среды с температурой Т1 в среду с температурой Т2 ≠ Т1. Постоянная времени τ термисторов составляет от 0,5 до 140 с. Основные характеристики термисторов приведены в табл. 3.2. В графе «Номинальное сопротивление» приведены крайние значения ряда номинальных сопротивлений.
Таблица 3.2
Параметры некоторых термисторов
Резисторы, имеющие большие значения ТКС в узком интервале температур, близком к температуре фазового перехода, получили название критезисторов. К ним относятся резисторы на основе двуокиси ванадия VO2, имеющие отрицате
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1177; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.100.218 (0.02 с.) |

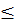 0,5, то приращение сопротивления за счет изменения геометрических размеров не превышает 2dl/l.
0,5, то приращение сопротивления за счет изменения геометрических размеров не превышает 2dl/l. = m dl/l, где m – константа, характеризующая изменение удельного сопротивления при деформации (иногда ее называют тензочувствительностью). При деформации удельное сопротивление твердого тела может изменяться вследствие следующих причин:
= m dl/l, где m – константа, характеризующая изменение удельного сопротивления при деформации (иногда ее называют тензочувствительностью). При деформации удельное сопротивление твердого тела может изменяться вследствие следующих причин: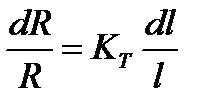 , (2.2)
, (2.2) – коэффициент пропорциональности между относительной деформацией
– коэффициент пропорциональности между относительной деформацией  и относительным изменением сопротивления
и относительным изменением сопротивления  .
.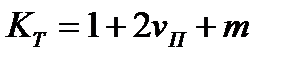 (2.3)
(2.3) , и тензоэффект определяется только изменением геометрии проводника. Так как в области пластической деформации
, и тензоэффект определяется только изменением геометрии проводника. Так как в области пластической деформации  , то
, то  для всех проводников одинаков и равен 2.
для всех проводников одинаков и равен 2.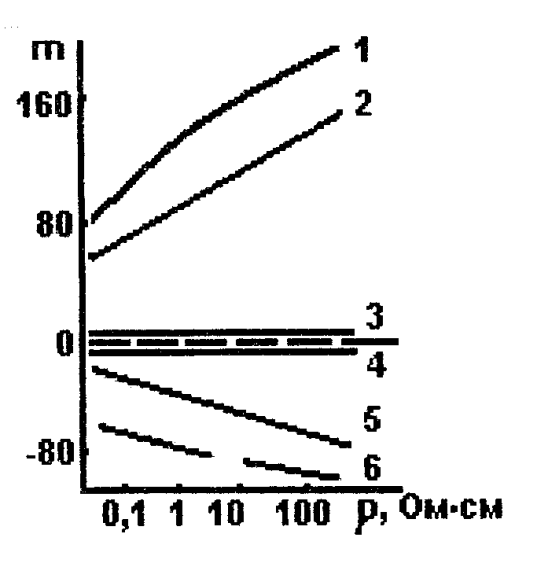
 -типа полупроводника
-типа полупроводника , (2.4)
, (2.4)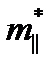 и поперечном
и поперечном 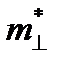 направлениях,
направлениях, 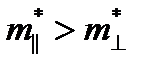 .Так как подвижность
.Так как подвижность 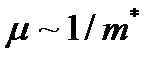 , то и значения подвижностей также различны и
, то и значения подвижностей также различны и 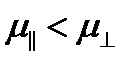 .
.
 0 = e(n1
0 = e(n1 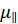 + n2
+ n2 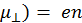 0μ0 , (2.5)
0μ0 , (2.5) – средняя подвижность.
– средняя подвижность.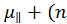 2 – Δn)
2 – Δn) 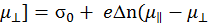 ). (2.6)
). (2.6)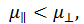 то σД
то σД 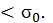 Относительное изменение проводимости
Относительное изменение проводимости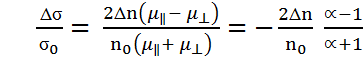 (2.7)
(2.7)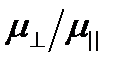 . В Si это отношение равно 5,16; в Ge – 19,3.
. В Si это отношение равно 5,16; в Ge – 19,3. , (2.8)
, (2.8) и
и  – соответственно концентрация и подвижность легких и тяжелых дырок, то
– соответственно концентрация и подвижность легких и тяжелых дырок, то , (2.9)
, (2.9) постоянна
постоянна  , определяется концентрацией акцепторной примеси и
, определяется концентрацией акцепторной примеси и 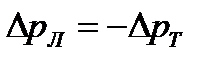 .
.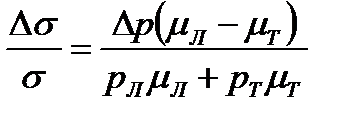 . (2.10)
. (2.10) ), p -InSb в направлении [111] (
), p -InSb в направлении [111] (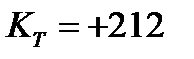 ).
).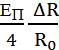 =
=  ΔT, (3.6)
ΔT, (3.6)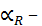 ТКС.
ТКС.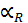 = 3,9·10 – 3(
= 3,9·10 – 3( -1 для термистора примем
-1 для термистора примем 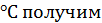 U = 1,9 мВ для платинового термометра и U = 25 мВ для термистора. Эти величины значительно превышают эдс термопар: 0,05 мВ для термопары железо-константан, 0,005 мВ – для термопары платинородий – платина.
U = 1,9 мВ для платинового термометра и U = 25 мВ для термистора. Эти величины значительно превышают эдс термопар: 0,05 мВ для термопары железо-константан, 0,005 мВ – для термопары платинородий – платина.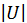 > 26 мВ можно пользоваться приближенными формулами для прямого и обратного токов
> 26 мВ можно пользоваться приближенными формулами для прямого и обратного токов