
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическая модель данных.Содержание книги
Поиск на нашем сайте В информационных мед.системах используются методы математической теории классификации и распознавания образов, в том числе применяется геометрическая модель данных. Данные – это числовые характеристики состояния объекта, например, состояние здоровья пациента. Для каждого признака используется соответствующая ось признаков, так что состояние объекта описывается точкой в пространстве признаков. В геометрической модели данных каждому объекту, т.е. образу, ставится в соответствие точка в пространстве признаков Х. Для оценки того, насколько близки между собой две реализации или два образа вводится понятие расстояния или степень близости. Будем считать пространство признаков метрическим. В нем можно ввести расстояние между точками М1 и М2:d(M1M2). Классификация в пространстве признаков заключается в разделении пространства признаков на классы Xi или области, содержащиеся в Х или пространство признаков Xi ϲ Х. Пусть Х1 – область (класс) х1 в пространстве признаков. Расстояние между точкой d(M1M2) и классом М называется точной нижней границей всех расстояний d между точкой М и Р Є к классу Х1. d1(М1,X1) = inf {d (M, P), для любых РєX1}, Расстояние между классами Х1 и Х2 называется точной нижней границей расстояний между точками М є классу Х1, Р є Х2. d2(Х1,Х2) = inf { d(М,Р), для любых МєХ1, РєХ2} Чем меньше расстояние между классами, тем больше между ними сходства. Используются сл.формулы вычисления расстояния: Пусть точка М1 задается радиус-вектором Х1 = {хi1, хi2, …, хiк}, а точка М2 радиус-вектором Х2 = {хj1, хj2, …, хjк}, Используются сл. формулы для вычисления расстояния меду точками: 1) 2) 3) 4) Используется при классификации распознавания образов. Примеры: Имеем медикодиагностическое изображение; заданы области контрастов, соответствующие определенной патологии. Тогда координатами в пространстве признаков будут значения интенсивностей R, G, B цветов и классификация заключается в разделении изображения на области с близкими цветовыми составляющими. Дано графическое медицинское изображение. Определить области, относящиеся к той или иной патологии, построив оболочку из патологических точек вокруг некоторого ядра. Геометрическое пространство образовано точками изображения. В качестве определяющих признаков используется совокупность данных медикобиологического исследования, например, температура, пульс, состав крови и мочи. В этом случае точки геометрической модели данных образуются из координат, являющихся результатами анализов, а классификация в пространстве признаков дает разделение точек пространства в соответствии с некоторыми заболеваниями. Решающие функции. Решающие или разделяющие функции используются для построения правил (решений), позволяющих определить принадлежность образов к некоторому классу. В мед. практике классификация и распознавание образов прим-ся при анализе рентгенограмм, томограмм и др. мед.диагностических изображений, в экспертных системах анализа электрокардиограмм, энцефалограмм. Существуют различные представления для решающих функций.
В виде линейной суммы: g(х) = w0 + w1х1 + w2х2 + … + wnхn
wi – весовые коэффициенты, каждый из которых характеризует вклад составляющей хi. Введем вектор
Тогда линейную решающую функцию можно записать в виде скалярного произведения: g( Решающее правило, сформулированное с помощью g(
P(
Если пространство признаков
P(
Необходимо иметь К решающих функций Кроме линейных используются квадратичные решающие функции: g( а также функции, построенные на поленомах различной степени
|
||
|
Последнее изменение этой страницы: 2016-08-25; просмотров: 611; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.007 с.) |

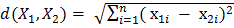 - Евклидово расстояние.
- Евклидово расстояние. - расстояние по Манхеттену.
- расстояние по Манхеттену. - расстояние по Чебышеву.
- расстояние по Чебышеву. - расстояние по Камберу.
- расстояние по Камберу. ={
={ 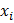 }, i=1,…,n.
}, i=1,…,n. = {w0, w1, w2, …, wn}, а к координатам вектора в пространстве признаков добавим нулевую координату х0 ≡ 1:
= {w0, w1, w2, …, wn}, а к координатам вектора в пространстве признаков добавим нулевую координату х0 ≡ 1: (
( ,
, .
.


