
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистичні характеристики мовних повідомленьСодержание книги
Поиск на нашем сайте Дослідження статистичних характеристик мовного сигналу базується на математичному представленні акустичного процесу утворення мови, який, у свою чергу, базується на фізичних процесах утворення мови. Розглянемо дискретну модель утворення мови (рис 1.25). В цій моделі можна виділити дві системи, модель збудження і модель випромінювання. Більшість звуків мови можна віднести або до вокалізованих (голосних), або до невокалізованих (приголосних). У випадку вокалізованих звуків джерело збудження повинно формувати квазіперіодичну послідовність імпульсів. У випадку невокалізованих – випадкові шумові коливання [2]. Структурна схема пристрою, який реалізує один із способів одержання такого сигналу, показана на рис.1.25. Вона складається з генератора імпульсної послідовності (ГІП) з періодом слідування імпульсів Для невокалізованих звуків модель збудження реалізується у вигляді генератора шуму (ГШ) з коефіцієнтом підсилення
Рис.1.25. Дискретна модель утворення мови Модель голосового тракту цілком характеризується передавальною функцією Передавальну функцію Ефект випромінювання мови можна описати за допомогою передавальної функції
Для управління такою моделлю повинна бути апріорна інформація про залежність відповідних параметрів (частоти основного тону, положення перемикача гучності та коефіцієнти передачі фільтрів) від часу. Для вокалізованих звуків, які повільно змінюються у часі, ця модель виявляється найбільш точною. Для невокалізованих звуків, які швидко змінюються, розглянута модель утворення мови може не відповідати реальним фізичним процесам. У будь-якому випадку припускається, що мовний процес, який є випадковим нестаціонарним процесом, повинен бути підданий короткочасному аналізу. Найчастіше вважають, що параметри моделі незмінні протягом 10...20 мс. Під час синтезу та аналізу систем передачі мови використовують різні абстрактні моделі мовного процесу, що в якійсь мірі відповідають реальній дійсності. Найбільш поширена модель являє собою нестаціонарний гауссівський випадковий процес з дисперсією та спектральною щільністю, що повільно змінюються. У разі використання такої моделі можна синтезувати систему зв’язку з найкращими характеристиками. Але при цьому виходить досить складна система, яка сама настроюється, синтез її досить складний, тому що відсутні численні статистичні характеристики таких моделей мовного процесу. Меншу точність має модель мовного сигналу, який являє собою нестаціонарний гауссівський процес з повільно змінюваною дисперсією та постійною усередненою спектральною щільністю, яка визначається експериментально з використанням усереднення за часом. Разом з тим, для реальних мовних процесів на досить великих відрізках часу задовольняються умови стаціонарності, що дає можливість розглядати мовний сигнал як квазістаціонарний. Для оцінки якості передачі мовного сигналу в цифрових системах передачі інформації широко використовуються різні апроксимації усередненої за часом щільності розподілу вірогідності розподілу мови (ЩВР) Найбільш зручною вважається така модель апроксимації ЩВР:
де Вважається, що вірогідності голосних Поряд з ЩВР важливе прикладне значення для аналізу систем передачі мови мають спектральні Найбільш поширена модель мовного процесу, який пройшов попереднє обмеження спектра за допомогою фільтра нижніх частот з частотою зрізу
Для аналізу пристроїв перетворення мови, наприклад у вокодерах, використовують апроксимацію у вигляді
Взагалі мовні випадкові процеси не є суттєво гауссівськими випадковими процесами.
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 339; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

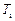 , який дорівнює періоду основного тону
, який дорівнює періоду основного тону 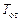 мовного сигналу. З виходу ГІП сигнал надходить на лінійну інерційну систему імпульсна характеристика
мовного сигналу. З виходу ГІП сигнал надходить на лінійну інерційну систему імпульсна характеристика  якої відповідає формі коливань в голосовій щілині. Коефіцієнт підсилення вокалізованого звуку
якої відповідає формі коливань в голосовій щілині. Коефіцієнт підсилення вокалізованого звуку  визначає інтенсивність голосового збудження.
визначає інтенсивність голосового збудження. , який регулюється. Так, у дискретному часі замість ГШ може бути використано генератор випадкових чисел, який формує послідовність із рівномірним спектром та довільною функцією розподілу.
, який регулюється. Так, у дискретному часі замість ГШ може бути використано генератор випадкових чисел, який формує послідовність із рівномірним спектром та довільною функцією розподілу.
 , полюси якої відповідають резонансам (формантам) мовного сигналу. Полюсна модель
, полюси якої відповідають резонансам (формантам) мовного сигналу. Полюсна модель  . Звичайно, моделі голосового тракту об’єднують разом. При цьому результуючу передатну функцію процесу утворення мови записують у вигляді
. Звичайно, моделі голосового тракту об’єднують разом. При цьому результуючу передатну функцію процесу утворення мови записують у вигляді .
. .
. ,
, ;
;  .
.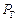 та приголосних
та приголосних 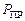 звуків однакові та дорівнюють 0,5.
звуків однакові та дорівнюють 0,5. та кореляційні
та кореляційні  характеристики.
характеристики.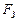 . Спектральна щільність потужності мовного процесу на виході такого фільтра визначається за співвідношенням:
. Спектральна щільність потужності мовного процесу на виході такого фільтра визначається за співвідношенням: ;
;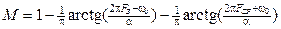 ; (1.52)
; (1.52)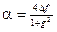 ;
;  ;
;  . (1.53)
. (1.53) ;
;  .
.


