
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Енергетичні характеристики звукового поляСодержание книги
Поиск на нашем сайте Звукова потужність це швидкість зміни роботи звукової хвилі А в напрямку поширення звукових хвиль через всю площу фронту хвилі. Фізично робота обумовлена опором середовища поширенню звукових хвиль. Звукова потужність визначається виразом
Інтенсивність (сила) звуку – це потік звукової енергії, що проходить в одиницю часу через одиницю поверхні фронту хвилі. Згідно визначення миттєве значення акустичної потужності дорівнює добутку миттєвих значень сили F і швидкості коливань v: P = Fv. Питома потужність звукових коливань. Питома потужність коливання визначається як
(1.3)
і називається силою звуку. Щільність звукової енергії ε являє собою середнє значення звукової енергії в одиниці об'єму середовища. Зв'яжемо поняття інтенсивності звуку і щільності енергії. Для цього виділимо об'єм середовища по напрямку поширення хвилі (рис. 1.9). Енергія в об'ємі середовища Δ V в розглянутий момент часу Δ W = ε Δ V = = ε Δ r Δ S піде з нього за час Δ t = Δ r / cзв, де cзв - швидкість звуку. Потік енергії Δ W Δ t = cзв ε Δ r Δ S/ Δ r = cзв ε Δ S. Підставивши цей вираз у формулу I =Δ W/ Δ S Δ t і виконавши відповідні перетворення, визначимо щільність звукової енергії ε = I/cзв. (1.4)
Плоска хвиля Плоска хвиля є випадком спрямованого випромінювання звуку джерелом, коли звукові промені паралельні один одному і перпендикулярні напрямку поширення. Паралельність променів вказує на те, що енергії не розходиться в просторі. При цьому фази звукових коливань будуть однакові в перпендикулярних напрямку поширенням звукових хвиль перетинах. Плоска хвиля виникає в тих випадках, коли розміри звукових випромінювачів більше довжини хвилі. В ідеальному випадку (при відсутності в'язкості середовища) інтенсивність звуку не повинна була б зменшуватися, але реально втрати існують. У розрахунках для невеликих відстаней зазвичай цими втратами нехтують. Нехай джерело випромінює плоску хвилю гармонійної форми рзв= рзв.m e jωt з нульовою початковою фазою. На деякій відстані r від джерела тиск внаслідок інерційності середовища буде запізнюватися по фазі на час τ = r/cзв і прийме значення рзв = рзв.m e jω(t-τ). (1.5) Введемо поняття хвильового числа k = ω/c = 2π/λ, яке визначає коефіцієнт зміни фази на одиницю відстані, а вираз (1.5) представимо у формі рзв = рзв.m e j(ωt-ωτ). З урахуванням того, що cзв = ω/k, а ωτ = ωr/с = ωrk/ω = kr, вираз (1.5) приймає більше зручну форму рзв = рзв.me j(ωt - kr). (1.6)
(1.7)
Порівняння виразів (1.6) і (1.7) показує, що звуковий тиск і коливальна швидкість в плоскій хвилі не мають зсуву по фазі.
(1.8)
де za = ρcзв називають питомим акустичним опором. Добуток питомої акустичного опору на всю площу поверхні акустичного випромінювача складає повний опір середовища (опір випромінювання): zR = za S = ρcзвS = pзвS/v = F/v (1.9) В силу відсутності зсуву по фазі між звуковим тиском і коливальною швидкістю опір випромінювання є активним. З введенням понять питомої акустичного опору і опору випромінювання вирази для сили звуку і випромінюваної акустичної потужності приймають вигляд: I = pзвv = v2 za = рзв.т 2/ za P = IS = v2 za S = v2zR. (1.10) Сферична хвиля
Сила звуку І1 на поверхні фронту сферичної хвилі (рис. 1.10) згідно визначається як
де P - випромінювана потужність, S 1 - площа фронту хвилі, r1 - відстань від центру випромінювача. На відстані r2 сила звуку
Рис. 1.10. Випромінювання сферичної хвилі
З двох останніх виразів випливає, що сила звуку в сферичної хвилі убуває назад пропорційно квадрату відстані від випромінювача. У просторі положення точки можна визначати в декартовій системі координат Х, Y, Z, або в полярній системі координат (рис. 1.11). В останньому випадку виходять більш прості вирази, оскільки положення довільної точки О в просторі визначається радіус-вектором r, азимутом Ψ і кутом Θ між радіусом-вектором і віссю Z. Так як фронт хвилі являє собою сферичну поверхню, то всі крапки середовища, що знаходяться на такій поверхні будуть коливатися синфазно з однаковою амплітудою. Значення амплітуди і фази коливань залежатимуть тільки від відстані від джерела звуку. Для довільного значення r можна записати вирази для звукового тиску рзв = рзв.me j(ωt - kr) (1.11)
З іншого боку згідно (1.10) I = рзв.т 2/2 za
Рис. 1.11. Визначення положення точки простору в різних системах координат Прирівнюючи вирази (1.10) і (1.12) для сили звуку, отримаємо
звідки визначимо амплітуду звукового тиску як
(1.14)
(1.15) Після інтегрування рівняння руху з урахуванням (1.15) і спрощення наведемо остаточний результат:
де фазовий зсув φ = arctg 1/kr Аналіз виразів (1.14) і (1.16) показує, що: 1. Амплітуди звукового тиску і коливальної швидкості обернено пропорційні відстані від випромінювача. Це пов'язано з тим, що площа фронту звукової хвилі збільшується в міру віддалення від випромінювача, а, отже, зменшується звукова енергія на одиницю площі. 2. Коливальна швидкість відстає по фазі від тиску. У ближній зоні (при виконанні умови r <<λ) фазовий зсув значний і у поверхні випромінювача φ = 90 °. У дальній зоні фазовим зрушенням можна знехтувати.
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 617; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 (1.2)
(1.2)
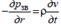

 Як випливає з раніше отриманого виразу (1.1) – а перша похідна за часом від коливальної швидкості – звідки з урахуванням (1.6) визначимо
Як випливає з раніше отриманого виразу (1.1) – а перша похідна за часом від коливальної швидкості – звідки з урахуванням (1.6) визначимо Якщо врахувати, що рзв = рзв.me j(ωt - kr) і cзв = ω/k,, то вираз (1.7) можна представити як
Якщо врахувати, що рзв = рзв.me j(ωt - kr) і cзв = ω/k,, то вираз (1.7) можна представити як Сферична хвиля у ідеальному випадку створюється пульсуючим шаром з радіусом R (рис. 1.10), звукова енергія якого поширюється рівномірно в усіх напрямках, або іншими словами - звукові промені у напрямку збігаються з радіусами сфери.
Сферична хвиля у ідеальному випадку створюється пульсуючим шаром з радіусом R (рис. 1.10), звукова енергія якого поширюється рівномірно в усіх напрямках, або іншими словами - звукові промені у напрямку збігаються з радіусами сфери.

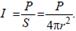 і для інтенсивності звуку (1.12)
і для інтенсивності звуку (1.12)

 (1.13)
(1.13) Підставивши (1.13) в (1.11) визначимо тиск в довільній точці простору:
Підставивши (1.13) в (1.11) визначимо тиск в довільній точці простору: Для визначення коливальної швидкості розглянемо виражения для рівняння руху (1.1) і звукового тиску (1.14). З рівняння руху випливає, що, а
Для визначення коливальної швидкості розглянемо виражения для рівняння руху (1.1) і звукового тиску (1.14). З рівняння руху випливає, що, а
 (1.16)
(1.16)


