
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерії надійності відновлюємих виробівСодержание книги Поиск на нашем сайте
Розглянемо наступну модель іспиту. Нехай на іспиті знаходиться N виробів, і нехай вироби, які відмовили негайно заміняються справними (новими або відремонтованими). Іспити вважаються закінченими, якщо число відмов досягає розміру, достатнього для оцінки надійності з визначеною довірчою ймовірністю. Якщо не враховувати часу, необхідного на відновлення системи, то кількісними характеристиками надійності можуть бути параметр потоку відмов w (t)і наробіток на відмову tср. Параметром потоку відмов називається відношення числа виробів, що відмовили за одиницю часу до числа випробовуваних виробів за умови: вироби, які вийшли зі строю заміняються справними (новими або відремонтованими). Відповідно до визначення:
де n (Dt)— число зразків, що відмовили, у інтервалі часу від t-Dt /2 до t+Dt /2; N — число випробовуваних зразків, Dt — інтервал часу. Вираз (2.1) є статистичним визначенням параметра потоку відмов. Параметр потоку відмов і частота відмов для ординарних потоків з обмеженою післядією пов'язані інтегральним рівнянням Вольтерра другого роду
По відомій a (t)можна знайти усі кількісні характеристики надійності невідновлюємих виробів. Тому (2.2) являється основним рівнянням, що зв'язує кількісні характеристики надійності невідновлюємих та відновлюємих виробів при миттєвому відновленні. Рівняння (2.2) можна записати в операторній формі:
Співвідношення (2.3) дозволяє знайти одну характеристику через іншу, якщо існують перетворення Лапласа функцій a (s) і w (s) та обернені перетворення виразів (2.3). Параметр потоку відмов має наступні важливі властивості: 1) для будь-якого моменту часу незалежно від закону розподілу часу безвідмовної роботи параметр потоку відмов більше, ніж частота відмов, тобто w (t) > а (t); 2) незалежно від виду функції a (t) параметр потоку відмов w (t)при t®¥ наближається до 1/ Tср. Ця важлива властивість параметра потоку відмов означає, що при тривалій експлуатації виробу, що ремонтується потік його відмов незалежно від закону розподілу часу безвідмовної роботи стає стаціонарним. Проте це зовсім не означає, що інтенсивність відмов є величина постійна; 3) якщо l (t)— зростаюча функція часу, то l (t)> w (t)> а (t), якщо l (t) — убутна функція, то w (t)> l (t)> а (t); 4) при l (t) ¹ const параметр потоку відмов системи не дорівнює сумі параметрів потоків відмов елементів. Ця властивість параметра потоку відмов дозволяє стверджувати, що при обчисленні кількісних характеристик надійності складної системи не можна сумувати наявні в даний час значення інтенсивностей відмов елементів, отримані по статистичним даним про відмови виробів в умовах експлуатації, тому що зазначені величини являються фактично параметрами потоку відмов; 5) при l(t)) = l = const параметр потоку відмов дорівнює інтенсивності відмов w(t)=l(t) = l. З розгляду властивостей інтенсивності і параметра потоку відмов очевидно, що ці характеристики різноманітні. В даний час широко використовуються статистичні дані про відмови, отримані в умовах експлуатації апаратури. При цьому вони часто опрацьовуються таким чином, що характеристики надійності, які приводяться, являються не інтенсивністю відмов, а параметром потока відмов w(t). Це вносить помилки при розрахунках надійності. У ряді випадків вони можуть бути значними. Для одержання інтенсивності відмов елементів із статистичних даних про відмови систем, що ремонтуються, необхідно скористатися формулою (1.4), для чого необхідно знати передісторію кожного елемента принципової схеми. Це може істотно ускладнити методику збору статистичних даних про відмови. Тому доцільно визначати l(t) по параметру потоку відмов w (t). Методика розрахунку зводиться до наступних обчислювальних операцій: — по статистичним даним про відмови елементів, виробів, що ремонтуються і по формулі (2.1) обчислюється параметр потоку відмов і будується гістограмма — гістограмма замінюється кривою, що апроксимірується рівнянням, — знаходиться перетворення Лапласа — по відомій — по відомій — знаходиться аналітичне вираження для інтенсивності відмов по формулі
— будується графік Якщо існує ділянка, де Приведена методика не може бути застосована, якщо не вдасться знайти по a (s)зворотне перетворення частоти відмов a (t). У цьому випадку приходиться застосовувати наближені методи рішення інтегрального рівняння (2.2) Рішення найбільше просто можна одержати за допомогою ЕОМ. Наробітком на відмову називається середнє значення часу між сусідніми відмовами. Ця характеристика визначається по статистичним даним про відмови по формулі
де t i— час справної роботи виробу між (i— 1)-ою та і - ою відмовами; п — число відмов за якийсь час t. З формули (1.12) очевидно, що в даному випадку наробіток на відмову визначається за даними іспиту одного зразка виробу. Якщо на іспиті знаходиться N зразків протягом часу t, тонаробіток на відмову обчислюється по формулі
де t i j — час справної роботи j-го зразка виробу між (i —1)-ою та i - ою відмовою; пj — число відмов за час t j-го зразка. Параметр потоку відмов і наробіток на відмову характеризують надійність ремонтуємого виробу і не враховують часу, необхідного на його відновлення. Тому вони не характеризують готовності виробу до виконання своїх функцій у необхідний час. Для цієї мети вводяться такі критерії, як коефіцієнт готовності та коефіцієнт вимушеного простою. Коефіцієнтом готовності називається відношення часу справної роботи до суми часів справної роботи та вимушених простоїв виробу, узятих за той самий календарний термін. Ця характеристика позначається Кг. Відповідно до даного визначення: К г = t p/(t p + t п), (2.7) де t p — сумарний час справної роботи виробу; t п— сумарний час вимушеного простою. Часи t pта t п обчислюються по формулах
де t р.i — час роботи виробу між (i— 1)-ою та i -ою відмовою; t п.i—час вимушеного простою після i -ої відмови; п — число відмов (ремонтів) виробу. Вираз (2.7) являється статистичним визначенням коефіцієнта готовності. Для переходу до ймовірного трактування, величини tp і tп заміняються математичними чеканнями часу між сусідніми відмовами і часу відновлення відповідно. Тоді К г = t ср/(t ср+ t в), (2.9) де t ср — наробітка на відмову; t в — середній час відновлення. Коефіцієнтом вимушеного простою називається відношення часу вимушеного простою до суми часів справної роботи і вимушених простоїв виробу, узятих за той самий календарний термін. Відповідно до визначення
або, переходячи до середніх величин, К п = t в/(t ср+ t в). (2.11) Коефіцієнт готовності та коефіцієнт вимушеного простою пов'язані між собою залежністю К п = 1 - К г. (2.12) При аналізі надійності відновлюємих систем коефіцієнт готовності обчисляють по формулі К г = Т ср/(Т ср + t в). (2.13) Формула (2.13) вірна тільки в тому випадку, якщо потік відмов найпростіший, і тоді t ср = Т ср. Часто коефіцієнт готовності, обчислений по формулі (2.13), ототожнюють з ймовірністю того, що в будь-який момент часу відновлюєма система справна. Насправді зазначені характеристики нерівноціні і можуть бути ототожнені при певних допущеннях. Дійсно, ймовірність виникнення відмови ремонтуємої системи на початку експлуатації мала. З ростом часу t ця ймовірність зростає. Це означає, що ймовірність застати систему в справному стані Для з'ясовування фізичного змісту коефіцієнта готовності КГ запишемо формулу для ймовірності застати систему в справному стані. При цьому розглянемо найбільш простий випадок, коли інтенсивність відмов і інтенсивність відновлення є величини постійні. Припускаючи, що при t =0 система знаходиться в справному стані (Р (0)=1), ймовірність застати систему в справному стані визначається з виражень:
де
Це вираження встановлює залежність між коефіцієнтом готовності системи та ймовірністю застати її в справному стані в будь-який момент часу t. З (2.14) очевидно, що PГ (t)® КГ при t ® ¥, тобто практично коефіцієнт готовності має сенс ймовірності застати вироб у справному стані при сталому процесі експлуатації. У деяких випадках критеріями надійності відновлюємих систем можуть бути також критерії надійності невідновлюємих систем, наприклад ймовірність безвідмовної роботи, частота відмов, середній наробіток до першої відмови, інтенсивність відмов. Така необхідність виникає завжди, коли має сенс оцінити надійність відновлюємої системи до першої відмови, а також у випадку, коли застосовується резервування з відновленням резервних пристроїв, що відмовили, у процесі роботи системи, причому відмова всієї резервованої системи не припускається.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 310; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.101.241 (0.007 с.) |

 (2.1)
(2.1) (2.2)
(2.2)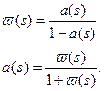 (2.3)
(2.3) ;
; функції
функції  частоти відмов;
частоти відмов; ;
; (2.4)
(2.4) .
. = const, то постійне значення інтенсивності відмов приймається для оцінки ймовірності безвідмовної роботи. При цьому вважається справедливим експоненціальный закон надійності.
= const, то постійне значення інтенсивності відмов приймається для оцінки ймовірності безвідмовної роботи. При цьому вважається справедливим експоненціальный закон надійності.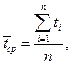 (2.5)
(2.5)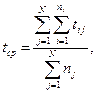 (2.6)
(2.6)
 , (2.8)
, (2.8) = t п/(t p + t п), (2.10)
= t п/(t p + t п), (2.10) (2.14)
(2.14)



