
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерії надійності невідновлюємих виробівСодержание книги Поиск на нашем сайте
Розглянемо наступну модель іспитів. Нехай на іспиті знаходиться N0 виробів. Іспити вважаються закінченими, якщо усі вони відмовили. Причому замість зразків, що відмовили, відремонтовані або нові не ставляться. Тоді критеріями надійності даних виробів являються: - ймовірність безвідмовної роботи P (t); - частота відмов а (t); - інтенсивність відмов l (t); - середній наробіток до першої відмови Тср. Ймовірністю безвідмовної роботи називається ймовірність того, що за певних умов експлуатації у заданому інтервалі часу або в межах заданого наробітку не станеться жодної відмови. Ймовірність безвідмовної роботи зі статистичними даними про відмови оцінюється виразом:
де N0 - число виробів на початку іспиту, n (t) - число виробів, що відмовилиза час t. На практиці іноді більш зручною характеристикою являється ймовірність відмови Q (t). Ймовірністю відмови називається ймовірність того, що за певних умов експлуатації в заданому інтервалі часу виникне хоча б одна відмова. Відмова і безвідмовна робота є подіями несумісними та протилежними, тому
Частотою відмов називається відношення числа виробів, що відмовили, в одиницю часу до початкового числа випробовуваних виробів за умови, що усі вироби, які вийшли зі строю не відновляються. Відповідно до визначення:
де n (Dt) - число зразків, що відмовили, в інтервалі часу від t-(t/2) до t+(t/2). Частота відмов є щільність ймовірності (або закон розподілу) часу роботи виробу до першої відмови. Інтенсивністю відмов називається відношення числа виробів, що відмовили, в одиницю часу до середнього числа виробів, які справно працюють у даний відрізок часу. Відповідно до визначення:
де Ncр = (Ni + Ni +1)/2 - середнє число справно працюючих виробів у інтервалі Dt; Ni - число виробів, що справно працюють на початку інтервалу Dt; Ni +1- число виробів справно працюючих наприкінці інтервалу Dt. Вираз (1.4) є статистичним визначенням інтенсивності відмов. Ймовірностна оцінка цієї характеристики знаходиться за допомогою вираза
Середнім наробітком до першої відмови називається математичне чекання часу роботи виробу до відмови. По статистичним даним про відмови середній наробіток до першої відмови обчислюється по формулі
де ti - час безвідмовної роботи i-го зразка; N0 - число випробуваних зразків. Як очевидно з формули (1.6), для визначення середнього наробітку до першої відмови необхідно знати моменти виходу зі строю усіх випробуваних елементів. Тому для обчислення Тср користуватися зазначеною формулою незручно. Маючи дані про кількість елементів ni, які вийшли зі строю у кожному i-му інтервалі часу, середній наробіток до першої відмови краще визначити з рівняння:
У виразі (1.7) tср . i і m знаходиться по наступних формулах: t ср.i=(t i-1+ t i)/2, m = t k/ Dt, де t i-1 — час початку i -го проміжку; t i— час кінця i -гопроміжку; t k — час, протягом якого вийшли зі строю всі елементи; Dt = ti-1 - ti - інтервал часу. При вивченні надійності технічних пристроїв найбільше часто застосовуються наступні закони розподілу часу безвідмовної роботи: експоненціальний, усічений нормальний, Релея, Гама, Вейбулла, логарифмічно-нормальний. З виразів для оцінки кількісних характеристик надійності очевидно, що усі характеристики, крім середнього наробітку до першої відмови, є функціями часу. Розглянуті критерії надійності дозволяють достатньо повно оцінити надійність невідновлюємих виробів. Вони також дозволяють оцінити надійність відновлюємих виробів до першої відмови. Наявність кількох критеріїв зовсім не означає, що завжди потрібно оцінювати надійність виробів по всім критеріям. Найбільш повно надійність виробів характеризується частотою відмов a(t). Це пояснюється тим, що частота відмов являється щільністю розподілу, а тому несе в собі усю інформацію про випадкове явище - час безвідмовної роботи. Середній наробіток до першої відмови являється достатньо наочною характеристикою надійності. Проте застосування цього критерію для оцінки надійності складної системи обмежено в тих випадках, коли: — час роботи системи набагато менше середнього часу безвідмовної роботи; — закон розподілу часу безвідмовної роботи не однопараметричний і для достатньо повної оцінки вимагаються моменти вищих порядків; — наявність системи резервування; — інтенсивність відмов непостійна; — час роботи окремих частин складної системи різний. Інтенсивність відмов - найбільш зручна характеристика надійності найпростіших елементів, тому що вона дозволяє більш просто обчисляти кількісні характеристики надійності складної системи. Найбільш доцільним критерієм надійності складної системи являється ймовірність безвідмовної роботи. Це пояснюється наступними особливостями ймовірності безвідмовної роботи: — вона входить у якості співмножника в інші, більш загальні характеристики системи, наприклад у ефективність і вартість; — характеризує зміну надійності у часі; — може бути отримана порівняно просто розрахунковим шляхом у процесі проектування системи й оцінена в процесі її іспиту.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.178.122 (0.007 с.) |

 ,(1.1)
,(1.1) (1.2)
(1.2)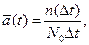 (1.3)
(1.3) (1.4)
(1.4) (1.5)
(1.5) , (1.6)
, (1.6) , (1.7)
, (1.7)


