Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вивести рівняння лінійної середньоквадратичної регресії y на х(х на Y). Пояснити зміст позначень. Дати означення коефіцієнту регресії , залишкової дисперсії та пояснити, що вони характеризують.Содержание книги
Поиск на нашем сайте
Лінійна середньоквадратична регресія Y на Х має вигляд g(X)=my+ Виведення: Введем у розгляд функцію двох незалежних аргументів F( Враховуючи, що М(Х – mx)=M(Y – my)=0, M[(X - mx)*(Y - my)]= μxy=r σxσy та виконав викладки, отримаємо F( Дослідим функцію F(
Звідси Легко впевнитися, що при цих значеннях g (X)= Коефіцієнт Підставимо знайдені значення Аналогічно можно отримати пряму середньоквадратичної регресії Х на Y X - mx=r Сформулювати теорему про корельованість складових нормально розподіленої двовимірної в.в. а) Мат. сподівання двохвимірної випадкової величини (X, Y) характеризує координати центру розподілу випадкової величини. Ці координати знаходять за формулами: Дисперсії DX та DY характеризують розсіювання випадкової точки (X, Y) вздовж координатних осей Ox та Oy, відповідно. Їх знаходять за формулами:
б) Условным мат. ожиданием ДСВ Y при X=x (x – определенное возможное значение X) называют произведение возможных значений Y на их условные вероятности: M(Y|X=x)= в) Для опису двохвимірної випадкової величини використовують також кореляційний момент (або коваріація): KXY=M((X-mX)(Y-mY))= г) коефіцієнт кореляції
Коэффициенттом корреляции rxy случайных величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин. Дати означення функції випадкової величи. Записати формулу для находження щільності імовірностей фун-ції неперервного випадкового аргумента. Навести приклади побудови розподілу фун-ції д.в.в. та щільності імовірностей фун-ції н.в.в. Н.В.В. Пусть х-действительное число. Вер-ть события, что Х примет значение, меньше х (Х <х), обозначим F(x)-фун-цией от х. Фун-цией распределения наз-ют фун-цию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньше х, т.е. F(x)=P(X<x). Геометр.смысл: F(x)-вер-ть того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х. Законом распределения дискр.случ.вел.есть соответствие между возможными значениями и их вероятностями. Задается таблично, аналитически, графически. Пример распределения фун-ции Д.В.В: В лотерее 100 билетов. Разыгрывают 1выигрыш в 50руб. и 10 выигр. По 1 руб. Найти Закон.распр.случ.величины Х-стоимости выигрыша для владельца одного билета. Решение: X: x Плотностью распределения вероятностей н.в.в. Х называют фун-цию f(x)-первую производную от фун-ции распределения F(x): f(x)= F’(x) Т.е. фун-ция распределения – первообразная для плотности распределения. Для описания распределения д.в.в. неприменима. Приклад: Дано: F(x)= 0, x<0 x2/81 0<x<=9 1 x>9 f(x)=F’(x) f(x)= 2x/81 x e (0;9] 0 x не належить (0;9] 2.25. Мат. сподівання ДВВ Х наз. число, яке = сумі добутків усіх можливих значень Х на відповідні їм імовірності. М(Х)= М(Х)= Дисперсією ДВВ Х наз. число, яке = мат. сподіванню квадрата відхилення ДВВ Х від її мат. сподівання. D(X) = M((X- M(X)) D(X) =
|
|||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 188; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.211.123 (0.01 с.) |

 (X – mx), де mx=М(Х), my=М(Y), σx=
(X – mx), де mx=М(Х), my=М(Y), σx=  , σy=
, σy=  , r=μxy/(σxσy) – коефіцієнт кореляції величин Х та Y.
, r=μxy/(σxσy) – коефіцієнт кореляції величин Х та Y. та
та  :
: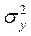 +
+  - 2r σxσy
- 2r σxσy  ,
,  σxσy=0
σxσy=0 ,
, 
 mx
mx X=
X=  -
- 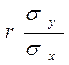 mx+
mx+  X, або g(X)=my+
X, або g(X)=my+ 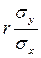 наз. коефіцієнтом регресії Y на X
наз. коефіцієнтом регресії Y на X (1 – r2). Величину
(1 – r2). Величину  (1 – r2) наз. залишковою дисперсією в.в. Y відносно в.в. Х..Вона характеризує величину похибки, яку допускають при заміні Y лінійної функції g(X)=
(1 – r2) наз. залишковою дисперсією в.в. Y відносно в.в. Х..Вона характеризує величину похибки, яку допускають при заміні Y лінійної функції g(X)= 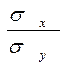 (Y- my), де r
(Y- my), де r  - коефіцієнт регресії Х на Y.Залишкова дисперсія
- коефіцієнт регресії Х на Y.Залишкова дисперсія 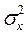 (1-r2) величини Х відносно Y.
(1-r2) величини Х відносно Y.


 Для непрерывных величин
Для непрерывных величин 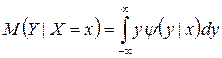 , где
, где  - условная плотность случайной величины Y при X=x.
- условная плотность случайной величины Y при X=x. . Корреляционным моментом μxy случайных величин X та Y называют мат. ожидание произведения отклонений этих величин. Для ДСВ:
. Корреляционным моментом μxy случайных величин X та Y называют мат. ожидание произведения отклонений этих величин. Для ДСВ:  Корреляционный момент служит для характеристики связи между величинами X и Y.
Корреляционный момент служит для характеристики связи между величинами X и Y. є кількісна характеристика залежності випадкових величин X та Y і часто використовуються в статистиці.
є кількісна характеристика залежності випадкових величин X та Y і часто використовуються в статистиці. =50, x
=50, x  =1, x
=1, x  =0. p
=0. p  =0,01
=0,01  =0,01
=0,01  =1(
=1( =0,89. Закон распределения Х(50,10,0), р(0,01;0,1;0,89).
=0,89. Закон распределения Х(50,10,0), р(0,01;0,1;0,89). для ДВВ
для ДВВ для НВВ
для НВВ ) для ДВВ
) для ДВВ