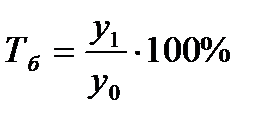Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Причины возникновения мультиколлиниарности.Содержание книги Поиск на нашем сайте 1. факторные признаки являются характеристикой одной и той же стороны явления. 2.Факторные признаки являются составляющими элементами друг друга. 3.Факторные признаки по экономическому смыслу дублируют друг друга. Устраняют мультиколлинеарность путем исключения из модели взаимосвязанных признаков либо путем их укрупнения. Качество уравнения регрессии зависит от степени достоверности и надежности исходных данных, а так же от объема совокупности. (минимум 7 наблюдений) Линейное уравнение множественной регрессии имеет вид:
Xn- факторные признаки y – среднее значение результативного признака. а1..n –коэффициенты регрессии (а0 не входит) Параметры уравнения могут быть определены графическим методом или методом наименьших квадратов. №4 Получив оценки корреляции и регрессии необходимо проверить их на соответствие истинным параметрам взаимосвязи. Для оценки значимости коэффициента парной корреляции рассчитывают стандартную ошибку коэффициента корреляции.
n - число наблюдений Полученное значение ошибки должно быть меньше коэффициента корреляции. Определяется расчетное значение t критерия.
Подобным образом на основе соответствующих формул рассчитывают стандартные ошибки и t критерий параметров уравнений и регрессий. Вывод о правильности выбора видов взаимосвязи и характеристика значимости всего уравнения регрессии делается с помощью F критерия путем определения его расчетного значения.
n – число наблюдений m- число параметров уравнения регрессии. Fрас должно быть >Fтеор при числе степеней свобод Если же неравенство не выполняется, следует пересмотреть формулу уравнения регрессии или перечень переменных. №5 При наличии соотношения между вариации признаков говорят об их ассоциации или взаимосвязанности, для определения тесноты связи двух качественных признаков каждая из которых состоит из двух групп, применяют коэффициенты ассоциации и контингенции. Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из явлений должно быть альтернативным. То есть состоящим из двух качественно отличных друг от друга значений признака. Таблица для вычисления коэффициентов ассоциации и контингенции.
Кк всегда меньше Ка, а взаимосвязь считается подтвержденный, если коэффициент ассоциации больше или равен 0,5 а коэффициент контингенции больше или равен 0,3 Лекция 10. Когда каждый из качественных признаков состоит более чем из 2-х групп, то для определения тесноты связи возможно применение коэффициентов взаимной сопряжённости Пирсона-Чупрова.
К1 – число значений (групп 1-ого признака) К2 – число значений (2-ого признака) Особое значение для оценки связи имеет биссериальный коэффициент корреляции, который даёт возможность оценить связь между качественным альтернативным и качественным варьирующим признаком.
y1,y2- среднее в группах
p- доля первой группы q-доля второй группы z-таблица значений z распределения в зависимости от p № 6. В анализе социально-экономических явлений часто приходится прибегать к различным условным оценкам с помощью рангов, а взаимосвязь между отдельными признаками измерять с помощью непараметрических коэффициентов связи. Ранжирование – процедура упорядочивания объектов изучения, которая выполняется на основе предпочтения, а ранг – это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической из соответствующих номеров мест. Такие ранги называют связными. Среди непараметрических методов оценки тесноты связи наибольшее значение имеют ранговые коэффициенты Спирмена и Кендалла. Эти коэффициенты могут быть использованы для определения тесноты связи, как между количественными, так и между качественными признаками.
Di^2 квадраты разности рангов n- число наблюдений Коэффициент Спирмена принимает значения от -1 до 1.
N – число наблюдений S – сумма разностей между числами последовательностей и числом инверсий по 2-ому признаку. Расчёт данного коэффициента (Кендалла) выполняется следующим образом: 1. Значения х ранжируется в порядке возрастания или убывания. 2. Значения у располагаются в порядке, соответствующем значениям х. 3. Для каждого ранга у определяется число следующего за ним рангов, превышающих его величину. Суммируя таким образом числа, определяют величину Р, как меру соответствия последовательностей рангов по х и у, и учитывают со знаком +. 4. Для каждого ранга у определяется число следующих за ним значений рангов, меньше его величины. Суммарная величина Q фиксируется со знаком -. 5. Определяется сумма баллов по всем членам ряда. Как правило, коэффициент Кендалла меньше коэффициента Спирмена. При достаточно большом объёме совокупности значение данных коэффициентов имеют следующую зависимость:
Связь между признаками считается статистически значимой, если значение коэффициентов Спирмена и Кендалла больше 0,5. Для определения тесноты связи между произвольным числом ранжированных признаков применяется множественный коэффициент ранговой корреляции – коэффициент конкордации.
m-количество факторов n-число наблюдений s-отклонения суммы квадратов рангов от средней квадратов рангов.
Тема 6. Ряды динамики и их применение в анализе социально-экономических явлений. 1. Понятие и правило построения рядов динамики. 2. Показатели анализа рядов динамики. 3. Компоненты временных рядов. 4. Способы определения основной тенденции и прогнозирования. 5. Применение моделей кривых роста. 6. Проверка адекватности выбранных моделей. 7. Характеристики точности моделей. 8. Анализ сезонных колебаний. №1. Процесс развития социально-экономических явлений во времени в статистике принято называть динамикой. Для отображения динамики строят ряды динамики, которые представляют собой ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке. Ряды динамики различают: 1. По времени: - моментные; - интервальные. 2. По форме представления уровней: - абсолютные; - относительные; - средние величины. 3. По расстоянию между датами или интервалами времени: - полные ряды (когда даты или периоды времени следуют друг за другом с равными интервалами); - неполные ряды (когда принцип равных интервалов не соблюдается). 4. По числу показателей: - изолированные ряды (когда анализируется 1 показатель); - комплексные ряды (когда в хронологическом порядке даётся система взаимосвязанных показателей). Правила построения рядов динамики: 1. Периодизация развития – расчленение его во времени на однородные этапы, в пределах которых показатель подчиняется одному закону развития. Периодизация может осуществляться несколькими методами: - исторический (опирается на значимые даты и события); - метод параллельной периодизации (когда качественному скачку показателя х соответствуют аналогичные изменения показателя у); - методы многомерного статистического анализа (когда анализ осуществляется на основе комплексных динамических рядов с использованием системы показателей для анализа сложных статистических явлений). 2. Статистические данные должны быть сопоставимы: по территории (данные по странам и регионам, границы которых изменились, должны быть пересчитаны в старых пределах); по кругу охватываемых объектов сравниваемые совокупности должны быть с одинаковым числом элементов; по единицам измерения; по ценам; по времени регистрации; по методологии расчёта.
Прежде чем анализировать динамический ряд необходимо убедиться в сопоставимости уровня ряда, и если она отсутствует добиться ее дополнительными расчетами. Для этого прибегают к приему смыкания рядов динамики. Под смыканием понимают объединение в один ряд более длинный двух или нескольких рядов динамики уровни которых исчислены по разной методологии или в разных территориальных границах. Смыкание рядов динамики
1 способ: пересчитывают данные за 2007-2010 годы с помощью коэффициента К=22,8/21,2=1,1 Этот коэффициент умножают на каждое значение, исчисленное по старой методике. 2 способ: уровни года, в котором произошли изменения, принимают за 100%, а остальные пересчитывают в проценты по отношению к этим уровням соответственно. 3. величины временных интервалов должны соответствовать интенсивности изучаемых процессов чем больше вариация уровней во времени, тем чаще следует делать замеры. Для стабильных процессов интервалы можно увеличить. 4. Числовые уровни рядов динамики должны быть упорядочены во времени. Не допускается анализ рядов с пропусками отдельных уровней. Если же пропуски неизбежны, то они восполняются условными расчетными значениями. №2 Для характеристики интенсивности изменения во времени используют следующие показатели: 1.абсолютный прирост 2.темп роста 3.темп прироста 4.абсолютное значение одного процента прироста. В случае, когда сравнение производится с периодом или моментом времени начальном ряду динамики получает базисные показатели. Если же сравнение производится с предыдущим периодом времени, то говорит о цепных показателях. Порядок расчета показателей динамики. 1.Абслютные приросты: а)базисные б)цепные таблица1 2.Темпы роста А) Б) 3.Темп прироста А) Б) 4. абсолютное значение одного процента прироста А) Б)
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |



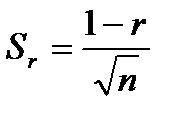

 для заданного уровня вероятности и числа степени свободы
для заданного уровня вероятности и числа степени свободы  , То можно утверждать …
, То можно утверждать …

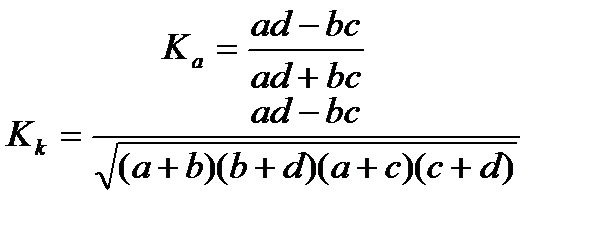
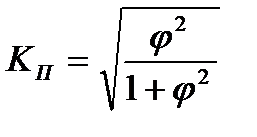
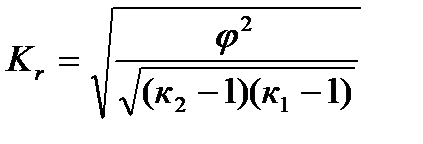
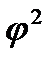 -Показатель взаимной сопряженности, который определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки. (-1)
-Показатель взаимной сопряженности, который определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки. (-1)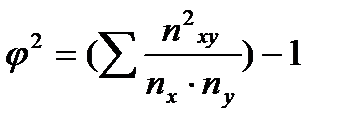
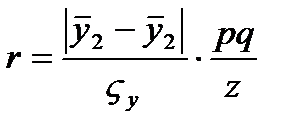
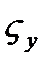 - среднее квадратическое отклонение фактических значений признака от их среднего уровня
- среднее квадратическое отклонение фактических значений признака от их среднего уровня