
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет, задачи, основные категории и понятия статистики.Содержание книги
Поиск на нашем сайте Предмет, задачи, основные категории и понятия статистики. 1. Предмет и метод. 2. Понятия и категории. 3. Задачи и организация. № 1. В настоящее время термин статистика употребляется в 3-ч значениях: 1.отрасль практической деятельности, 2.цифровой материал, служащий для характеристики, какой-либо области общ. Знаний и явлений. 3.отрасль знаний, научная дисциплина. Предмет: количественная сторона массовых общественных явлений в неразрывной связи с их качественной стороны и количественное выражение закономерностей общ. Развития в конкретных условиях места и времени. Для получения статистической циф-ы органы государства и ведомственной статистики, коммерческие структуры проводят различного рода статистические исследования. Процесс стат. исследования включает 3 стадии: 1.сбор данных; 2.их сводка и группировка 3. Расчет анализ обобщающих показателей. Под стат. методологией понимается система приемов способов и методов, направленных на изучение количественных закономерностей. Методы: -статистические группировки -средние величины и показатели вариаций -выборочное наблюдение -карреляция -ряды динамики -индексы № 2 Свой предмет статистика изучает при помощи опред. категорий (понятий, которые отражают наиболее общие и существ. свойства, признаки, связи и отношения предметов и явлений объективного мира) Категории: 1. Статистическая совокупность – совокупность социально-экономических объектов или явлений общественно жизни, объединенных качественной основой, но отличающихся отдельными признаками могут быть однородными и неоднородными. Однородная – один или несколько признаков (существенных) объектов является общим для всех единиц. Совокупность, в которую входят явления разного типа – разнородия. 2. Единица совокупности – первичный элемент стат.совокупности, являющиеся носителем признаков, подлежащих регистрации и основой ведущегося при обследовании счета. 3. Признак – качественная особенность единицы совокупности. По характеру отображения свойств единиц изучаемой совокупности признаки делятся на имеющиеся непосредственное количественное выражение (возраст, стаж) и не имеющие его (единицы различаются по содержанию – профессия) – атрибутивные признаки. Если имеются противоположные по назначению варианты признака, говорят об альтернативном признаке. 4. Стат. показатель - понятие, отображающие количественные характеристики. Соотношения признаков общественных явлении. Могут быть объемными (численность) и расчетными (средний заработок). Могут быть плановыми, отчетными и прогностическими. Надо отличать от данных! Данные – конкретные числовые значения стат.показателей. Они определены не только качественно, но и количественно и зависят от условий, места и времени. 5. Система статистических показателей - совокупность статистических показателей, отражающая взаимосвязи, которые объективно существуют между явлениями. Охватывает все стороны жизни общества на различных уровнях: на уровне страны, региона – макроуровень, или на уровне семьи, фирмы – макроуровень. Система статистических показателей имеет особенности: 1.носят исторический характер - меняются с обществом. 2.методология расчетов статистических показателей совершенствуется. … ………………………………………………………………………………………………………………………………………………. Деятельности федеральных и региональных органов власти, анализ стат.инфы и ее системат. публикация. В соответствие с административным делением РФ образована система местных органов соц.статистики. В республиках РФ имеются республиканские статистические комитеты, в областях, краях- территориальные гос. комитеты, по статистии в районах и городах – управления, отделы. Средние величины и показателей вариации. 1.Абсолютные и относительные величины. 2.Средняя величина и ее сущность. Виды средних величин и способы их вычисления. 3.Основные показатели вариаций 4.Неиспользование показателей вариации в анализе взаимосвязей. 5.Понятия о закономерностях распределения. №1 Абсолютными статистическими величинами называют первичные обобщающие показатели характеризующие размеры общественных явлений в конкретных условиях места и времени. Абсолютные величины выражают размеры общественных явлений в определенных единицах измерения: трудовых, стоимостных и натуральных?? Натуральным и называется единица измерения, которая выражает размеры тех или иных явлений в физических мерах то есть мерах веса (кг,га,т). Что бы измерить объем однородной, но не одинаковой продукции используют условно натуральные единицы измерения. Стоимостными называются единицы измерения, которые используют для выражения объема разнообразной продукции в денежной форме. Трудовая единица измерения используется для учета затрат рабочего времени и определенного уровни производимости труда. В некоторых случаях применяют комбинированные единицы измерения(тонны километры) Различают индивидуальные и итоговые величины, которые служат для характеристики количественных признаков отдельных единиц и всех единиц изучаемых совокупности соответственности.
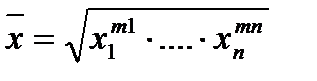
Сама по себе абсолютная величина не дает полного представления об изучаемом явлении не показывает его структуру соотношения между отдельными частями и развитии во времени. Все эти функции выполняют определяемые на основе абсолютных, относительные величины. Относительная величина в статистике – это обобщающий показатель, который дает числовую меру соотношения двух сопоставляемых абсолютных величин. Величина с которой производится сравнение называется базой сравнения и в зависимости от того какому значению приравнивается база сравнения различаются следующие формы выражения относительных величин: 1. Коэффициент – база принимается за единицу. 2. Процент – база принимается за 100. 3. Промилле – база принимается за 1000 (‰) 4. Продецимилли – база принимается за 10000.(‰0) Проценты, как правило, используются в тех случаях когда сравниваемый абсолютный показатель превосходит базисный не более чем в два три раза. Проценты более 200-300 заменяют кратным соотношением. Если базисный показатель превышает сравниваемый более чем в 1000 раз удобно использовать промилле, то есть тысячную долю числа. В расчете на 10000 человек населения определяется численность студентов вузов, численность врачей, уровень заболеваемости. По своему содержанию относительные величины делятся на следующие виды: 1. Относительные величины планового задания. Определяют соотношение плановой величины к фактической величине прошлого периода К=Упл2012/Уф2011. 2. Относительные величины выполнения планов – это отношения фактической величины отчетного года к плановой величине этого же года Квып=Уф2012/Упл2012. 3. Относительные величины динамики или роста – это отношения изучаемой величины за данный период к одноименной величине за прошлый период Кдин=Уф2012/Уф2011. Кдин=Кплз*Квып 4.Относительные величины структуры – вычисляются путем деления каждой части целого на общий итог и выражаются в процентах. 5. Относительные величины координации – это соотношения между отдельными частями одного и того же целого. 6. Относительные величины сравнения – это показатели характеризующие отношение величины признака данного объекта к одноименно величине другого объекта. По мимо перечисленных, используют сложные относительные величины, что бы показать влияние отдельных составных частей на изменение явления в целом. Виды средних величин. 1. Средняя арифметическая простая – применяется в тех случаях, когда имеется значения признака по каждой единицы совокупности или когда каждое значение признака встречается одинаковое число раз. В статистике изучение изучаемого признака называются вариантами и обозначаются Х1..Хn. Х̄̄=(Х1+..+Хn)/n n – число вариантов 2. среднее арифметическое взвешенное - исчисляется, когда значение признака встречается не одинаковое число раз или по сгруппированным данным. Х̅=(Х1*f1+…+Хn*fn)/(f1+..+fn) 3. Средне гармоническая - представляет собой обратную величину средней арифметической из обратных величин. Применяется в тех случаях, когда имеются данные об индивидуальных значениях усредняемого признака и общем объеме совокупности, но не известные чистоты или веса(f) X̅=∑W/∑(W/x) где Wi=Xi*fi выручка, цена, кол-во. 4. Средняя хронологическая – применяется в рядах динамики. X̅=(1/2*X1+X2+X3+..+1/2Xn)/n-1 5. Средняя геометрическая – также используется в рядах динамики и так же как средне арифметическая может быть просто и взвешенной.
6. Средняя квадратическая -применяется при расчете показателей вариации.
7. Структурная среднее: мода и медиана. Мода – модой называется наиболее часто встречающаяся величина признака. В интервальном вариационном ряду формула моды выглядит следующим образом.
Где х0-нижняя граница модального интервала(модальный-интервал с наибольшей численностью) i-величина интервала F1 – величина интервала предшествующая… F2- чистота модального интервала F3 –чистота интервала следующего за модальным интервалом. (таблица) Медианой называется величина признака, которая находится в середине упорядоченного вариационного ряда. Где варианты расположены в порядке возрастания или убывания, если число членов ряда нечетное медианой будет средний член ряда по порядку. Если число членов ряда четное медианой является среднее арифметическая простая из двух вариант находящихся в середине ряда. В случае интервальных вариационных рядов, медиана рассчитывается по формуле:
Гдех0-нижняя граница медианного интервала i-величина медианно интервала М- численность всех совокупности S - сумма накопленных частот интервалов предшествующих медианному. Хме- чистота медианного интервала. Для того что бы определить в каком интервале находится медиана необходимо найти сумму накопленных частот интервалов превосходящую половину численности совокупности. Численность совокупности это число объектов, которые мы подвергаем исследованию. Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше чем от другой любой величины. Если мода отражает типичный наиболее распространенный вариант значений признака, то медиана практически выполняет функции средней для неоднородной совокупности.Она так же используется, когда среднее не позволяет оценить исследуемую совокупность в следствии сильного влияния максимальных минимальных значений. №3 Средняя арифметическая сама по себе не достаточно для обобщающей характеристики совокупности. В средней отражаются общие условия присущие всей данной совокупности, но не отражаются индивидуальные частные условия порождающие вариацию отдельных единиц совокупности. Вариация - отклонение индивидуальных значений от средней. Для обобщающей характеристики колеблимости или вариаций используют следующие показатели: размах вариаций, средние линейные отклонения, среднее квадратическое отклонение, дисперсия, и коэффициент вариаций. Размах вариаций представляет собой разность между наибольшим и наименьшим значениями признака R=Xmax-Xmin. Средние линейные отклонения представляют собой среднею из абсолютных величин отклонений всех значений от их средней арифметической.
n-число вариантов. Среднее квадратическое отклонения представляет собой корень квадратный из дисперсии. Дисперсия - средний квадрат отклонений индивидуального значения признака от их средней величины. Среднее квадратическое отклонение так же как среднее линейное отклонение рассчитывается по простой или взвешенной формуле, выбор которой зависит от способа расчета средней арифметической
(если расчет дисперсии)
Среднее квадратическое отклонение показывает абсолютную меру колеблимости признака в тех же единицах измерения, что и средней величины, но оно не может служить для сравнения показателей колеблимости по различным совокупностям с этой целью используют следующий показатель коэффициент вариаций, который представляет собой отношения среднего квадратического отклонения к средней арифметической.
Если значение коэффициента вариаций меньше 33 % то совокупность по рассматриваемому признаку можно считать однородной. №4 Показатели вариаций могут быть использованы не только в анализе колеблемости изучаемого признака, но и в оценки степени воздействия одного признака на вариацию другого признака, то есть в анализе взаимосвязей между показателями. При проведении такого анализа исходная совокупность должна представлять собой множество единиц каждая из которых характеризуется двумя признаками: факторным и результативным. Факторным называется признак оказывающий влияние на взаимосвязанный с ним признак. Признак, поддержанный влиянию, называется результативным. Для выявления взаимосвязи исходная совокупность делится на две и более групп по факторному признаку. Выводы о степени взаимосвязи базируются на анализе вариации результативного признака, при этом применяется правило сложения дисперсий.
Средняя из внутри групповых дисперсий выражает ту часть вариаций результативного признака, которая обусловлена действием всех прочих неучтенных факторов. Кроме фактора по которому осуществлялась группировка.
Межгрупповая дисперсия отражает, ту часть вариаций результативного признака, которая обусловлена воздействием факторного признака. Это воздействие проявляется в отклонении групповых средних от общей средней.
x̅i-среднее значение результативного признака i-той группе x̅0- среднее значение результативного признака по совокупности в целом (общее среднее) ni- объем или численность i- той группе Если факторный признак, по которому производилась группировка не оказывает никакого влияния на результативный признак групповые средние будут равны между собой и совпадут с общей средней. В этом случае межгрупповая дисперсия будет равно нулю. Теснота связи между факторным и результативным признаками оценивается на основе эмпирического корреляционного отношения.
Данный показатель может принимать значения от 0 до 1, чем ближе к единице будет его величина, тем сильнее связь между рассматриваемыми признаками. Ряды распределения представляют собой простейшую группировку, в которой каждая выделенная группа характеризуется одним показателем. Статистический ряд распределения это упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку. В зависимости от признака положенного в основу ряда распределения различают атрибутивные( не имеют количественного выражении) и вариационные ряды распределения. Вариационные рядами называют ряда распределения, построенные по количественному признаку. В зависимости от характера вариаций признака различают дискретные и интервальные вариационные ряды. Дискретный вариационный ряд характеризуют распределения по дискретному признаку, принимающему только целые значения. (количество детей, 0,1,2,3) Построение интервальных вариационных рядов целесообразно, прежде всего, при непрерывной вариации признака, а так же если дискретная вариация проявляется в широких пределах, то есть число вариантов дискретного признака достаточно велико. Правило построения рядов распределения аналогичны правилам построения группировки. Анализ рядов распределения наглядно можно проводить на основе графического изображения: полигон – этот график используется для дискретных рядов. (8 график)
Гистограмма - строится для интервальных рядов. Кумулята – график накопленных частот. (9 график)
Огива – график схожий с кумулятой, если у кумуляты поменять местами оси X и Y. При проведении группировки можно заметить определенную зависимость между изменений значений варьирующего признака и частот. Частоты с увеличением значений варьирующего признака первоначально увеличиваются, а затем после достижения максимальной величины середины ряда уменьшаются. Такие закономерности изменения частот в вариационных рядах называются закономерностями распределения. (10график) Под кривой распределения понимается графическое изображение в виде непрерывной линии изменений частот в вариационном ряду, функционально связанного с изменением вариантов. В статистической практике встречаются следующие разновидности кривых распределения. 1.одновершинные кривые, которые могут быть семетричными, умеренно асиметричными и крайне ассиметричными. 2.Многовершинные кривые. Для однородных совокупностей, как правило характерны одновершинные распределения. Многовершинность свидетельствует о неоднородности совокупности и в таком случае необходимо перегруппировка данных с целью выделения более однородных групп. Выяснения общего характера распределения предполагает оценку его однородности, а так же вычисления показателя асимметрии. Для симметричных распределений частоты любых двух вариант равно отстоящих в обе стороны от центра распределения равны между собой, а так же равны среднее, мода и медиана. Х=М0=Ме При сравнительном изучении асимметрий нескольких распределений с разными единицами измерения вычисляется относительный показатель асимметрии.
Если коэффициент асимметрии положительный имеет место правосторонняя асимметрия, если отрицательный – левосторонний. Если коэффициент асимметрии больше 0,5 независимо от знака – асимметрия значительна. Если меньше 0,25 асимметрия не значительна. Выборочное наблюдение 1. Основные теоретические положения выборочного метода. 2. Виды выборки. 3. Ошибки выборочного наблюдение и их вычисления. 4. Определения необходимой численности выборки. 5. Оценка результатов выборочного наблюдения и распространение на генеральную совокупность. 6. Малая выборка. №1 Выборочным называется такое наблюдение, которое дает характеристику всей совокупности на основе обследования некоторые ее части. Выборочный способ имеет ряд преимуществ перед сплошным. 1. необходимые сведения нужно получить с меньшими затратами материальных средств. 2. меньше затрат рабочего времени. 3. В ряде случаев статистическое наблюдение можно провести только путем выборочного обследования. При выборочном способе допускается меньше ошибок регистрации. При проведении выборочного обследования необходимо соблюдать следующие положения. 1. Для каждой единицы должна обеспечиваться равная возможность попасть в выборку. 2. численность выборки должна быть достаточно большой, что бы результаты были надежными. Причем достаточно большой считается 10% выборка. При выборочном наблюдении анализируют генеральную и выборочную совокупность. Генеральной совокупностью называется общая масса единиц данного рода из которой производят отбор некоторой части для обследования. Выборочная совокупность представляет собой массу единиц данного рода, отобранных из генеральной совокупности для выборочного обследования. Выборочные наблюдения широко используются во первых для статистической оценки и проверки гипотез, то есть применяется в науке. Во вторых, для решения производственных и управленческих задач. 3.при отраслевых социально-экономических исследований. 4.для решения задач сфере предпринимательской деятельности. №2 В зависимости от способа отбора различают следующие виды выборочного наблюдения. 1.собственно случайное наблюдение 2.механическое 3.типическое 4.серийное Причем все они могут быть повторными и без повторными. Повторным называется отбор, при котором ранее отобранные единицы после записи ее признаков возвращаются в генеральную совокупность и снова участвуют в выборки. Без повторный это способ отбора, при котором ранее отобранная единица больше не возвращается в генеральную совокупность и в дальнейшей выборке не участвует. 1) Собственно случайно называется отбор, при котором каждая единица имеет равную возможность попасть в выборку. При этом формирование выборочной совокупности чаще всего производится путем жеребьевки. Однако применение жеребьевки связано с значительными затратами, кроме того не всегда возможно заранее составить перечень единиц совокупности, поэтому применяют один из следующих способов. 2) механический отбор, представляет собой разновидность случайного отбора заключается в том что отбор единиц производится в каком либо механическом порядке. 3) типическим называется отбор, при котором генеральная совокупность предварительно разбивается на более или менее однородные группы, из которых в случайном порядке производят отбор необходимой численность единиц, либо случайным либо механическим способом, но при этом важно соблюдать пропорции. 4) серийным называется такой отбор, при котором единица совокупности забираются сериями, а внутри серии проводится сплошное обследование. На практике различные виды выборочного наблюдения используется не в чистом виде, а в различных сочетаниях(напрмер, случайные и механические). Таким образом, получаем комбинированный отбор. Многоступенчатый отбор, когда их генеральной совокупности сначала извлекаются укрупненные группы, затем более мелкие и так до тех пор пока не будут отобраны те единицы, которые подвергаются обследованию. №3 Ошибки репрезентативности свойственны только выборочному наблюдению и представляют собой величину расхождения между сводными показателями генеральной и выборочной совокупности. Предельные ошибки. Причем формулы отдельных ошибок отличаются от разного типа отборов. Типический отбор Для типической выборки вместо общей дисперсии по всей выборочной совокупности, берется среднее из частных дисперсий, каждой группы, то есть средние величины из соответствующих частных показателей выборочной совокупности. ( А)повторный отбор для средней Для доли Б) без повторный отбор Для средней Для доли Серийный отбор. А) повторный отбор Для средней Для доли Б) безповторный отбор. Для средней Для доли N –со значком s общее количество равно великих серий генеральной совокупности. ns количество серий отобранных для обследования. Ws доля данного признака в среднем по всем обследованным группам. Сигма ^2 s - межгрупповая дисперсия.
№4 При организации выборочного наблюдения важное значение имеет правильное определение необходимой численности выборки. Превышение численности выборки увеличивает затраты на нее. Если численность выборки на достаточно, могут быть значительные погрешности. чИсленность выборки зависит, чем больше колеблимость, тем больше должна быть численность выборки и наоборот. Обратная связь существует между численностью выборки и ее предельной ошибкой для получения меньшой ошибки требуется большая численность выборки. Численность выборки зависит от способа отбора. Пример.
Прямая. Графический метод. Взаимосвязь между признаками изображается с помощью поля корреляции. (1)(график)
При отсутствии тесных связей имеет место беспорядочное расположение точек на графике, чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи. Для социально-экономических явлений характерно, что наряду с существенный факторами формирующими уровень результативного признака, на него оказывают воздействие многие другие неучтенные случайные факторы, это свидетельствует о том, что взаимосвязь явлений носит корреляционный характер. Корреляция – это статистическая зависимость между случайными величинами не имеющие строго функционального характера, при которой изменения одной из случайных величин приводит к изменению математического ожидания другого. Различают следующие виды корреляции: 1.Парная корреляция -Это связь между двумя признаками, результативным и факторным, или между двумя факторными 2.Частная корреляция это зависимость между результативным и одним факторными признаками, при фиксированном значении других признаков. 3.Множественная корреляция – это зависимость результативного и двух и более факторных признаков включенных в исследование. Корреляционный анализ имеет свои задачи, количественные определения тесноты связи между признаками Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменения зависимой величины или результативного признака, обусловлено влиянием одной или нескольких независимых величин или факторов. №2 1 способ: Простейшим видом корреляционным связи, является связь между двумя признаками, результативным и факторным. Такая связь называется парной корреляцией и ее можно выразить уравнением прямой линии: B – Коэффициент пропорциональности или регрессии, показывающий на сколько единиц в среднем изменится результативный признак, при изменении факторного признака на одну единицу, значение параметров а и b определяется способом наименьших квадратов путем построения и решения системы двух нормальных уравнений.
Где n – число членов в каждом из двух рядов. Соответствующее значение подставляют в систему уравнений, пользуясь расчетами, проведенными во вспомогательной таблице.
Должно быть минимум 7 наблюдений. n-3 По мимо коэффициента регрессии определяют тесноту или силу связи с помощью коэффициентов корреляции и коэффициента детерминации. Коэффициент корреляции представляет собой величину, которая изменяется в пределах от нуля до -+1. В тех случаях, когда коэффициент корреляции равен нулю, связь отсутствует. Если же равен +или- 1, связь между факторным и результативным признаками функциональная. Знак при коэффициенте корреляции указывает на направление связи, + связь прямая, - обратная. Исчисляют коэффициент корреляции по формуле: Сигма x y –отклонения Коэффициент детерминации D=r^2 Коэффициент детерминации показывает, на сколько процентов вариация результативного признака объясняется колебаниями факторного признака. Данный способ вычисления параметров парной линейной корреляции применяется я в том случае, если исходные данные приведены, по различным объектам, Если же исходная информация представлена в динамике, то есть за несколько периодов времени или на несколько дат, применяется второй способ.
Минимум 7 наблюдений.
Если коэффициент регрессий равен 1,5, значит при увеличении производительности труда (т е фактического признака) на 1000 руб, то Прибыль возрастет на 1,5 тыс руб. Коэффициент корреляции. Вывод: так как r=0.8 то полученное значение коэффициента корреляции позволяет утверждать, что между прибылью и производительностью труда существует прямая тесная взаимосвязь. D=r^2=0,64 Вывод: Значение коэффициента детерминации показывает, что вариация прибыли на 64 % объясняется колебаниями производительности труда. С целью расширения возможности экономического анализа, рассчитывают коэффициент эластичности бета- коэффициент. Если Э=1,1, то коэффициент эластичности показывает, на сколько процентов изменится значение результативного признака, при изменении факторного признака на 1 %. Вывод: коэффициент эластичности свидетельствует о том, что при увеличении производительности труда на 1 %прибыль возрастет на 1,1%.
бета- коэффициент он показывает, на сколько средних квадратических отклонений изменится результативный признак, при изменении факторного признака на одну сигму. Допустим равна 1,8, при увеличении производительности труда на одно средне квадратическое отклонение прибыль возрастет на одну 1,8 сигма. В случае наличия линейной или не линейной зависимости между двумя признаками для измерения тесноты связи применяют так называемое корреляционное отношение. Различают эмпирическое и теоретическое корреляционное отношение. Эмпирическое корреляционное отношение рассчитывается по данным группировки, когда
Причем все эти дисперсии рассчитываются по результативному признаку. Таблица для вычисления коэффициентов ассоциации и контингенции.
Кк всегда меньше Ка, а взаимосвязь считается подтвержденный, если коэффициент ассоциации больше или равен 0,5 а коэффициент контингенции больше или равен 0,3 Лекция 10. Когда каждый из качественных признаков состоит более чем из 2-х групп, то для определения тесноты связи возможно применение коэффициентов взаимной сопряжённости Пирсона-Чупрова.
К1 – число значений (групп 1-ого признака) К2 – число значений (2-ого признака) Особое значение для оценки связи имеет биссериальный коэффициент корреляции, который даёт возможность оценить связь между качественным альтернативным и качественным варьирующим признаком.
y1,y2- среднее в группах
p- доля первой группы q-доля второй группы z-таблица значений z распределения в зависимости от p № 6. В анализе социально-экономических явлений часто приходится прибегать к различным условным оценкам с помощью рангов, а взаимосвязь между отдельными признаками измерять с помощью непараметрических коэффициентов связи. Ранжирование – процедура упорядочивания объектов изучения, которая выполняется на основе предпочтения, а ранг – это порядковый номер значений признака, расположенных в порядке возрастания или убывани
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 353; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.021 с.) |

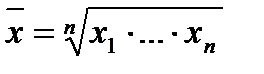
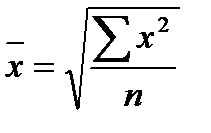
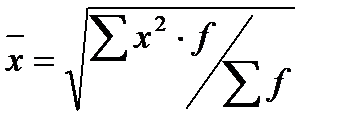
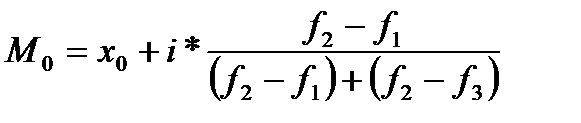
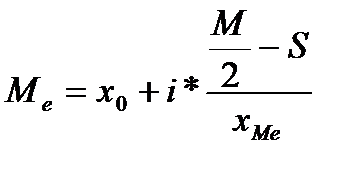
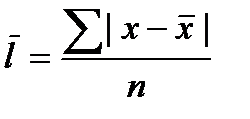 простая
простая
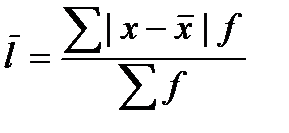 взвешенная f-веса
взвешенная f-веса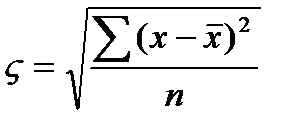
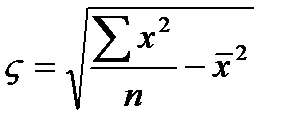
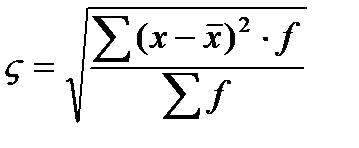 средняя квадратическая взвешенная
средняя квадратическая взвешенная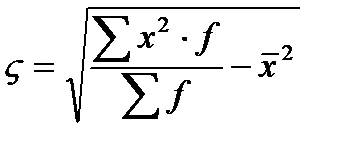
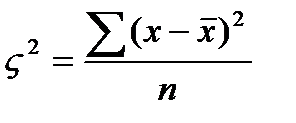
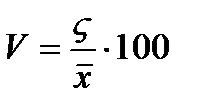 выражается в процентах.
выражается в процентах.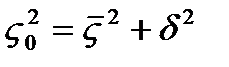 общая дисперсия, средняя из внутригрупповых дисперсий, межгрупповая дисперсия(дельта).
общая дисперсия, средняя из внутригрупповых дисперсий, межгрупповая дисперсия(дельта).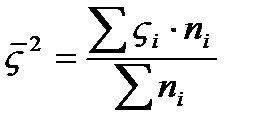 колебания среднего р. рабочих активов= дисперсия результативности признака в i-той группе, ni – объем или численность.
колебания среднего р. рабочих активов= дисперсия результативности признака в i-той группе, ni – объем или численность.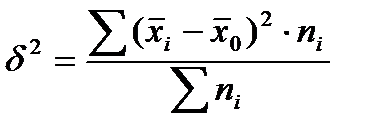
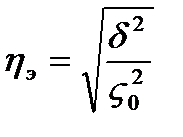
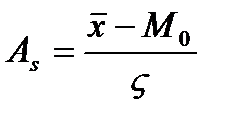
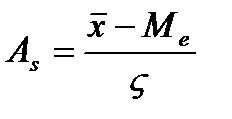
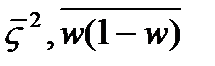 )
)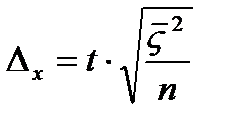 t-коэффициент доверия, то есть величина показывающая вероятность ошибки. Определяется по таблицам Стьюдента.
t-коэффициент доверия, то есть величина показывающая вероятность ошибки. Определяется по таблицам Стьюдента.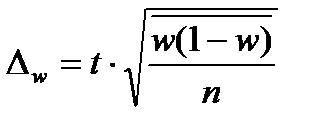
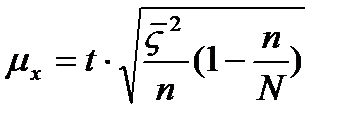
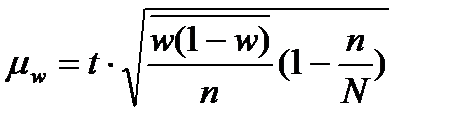
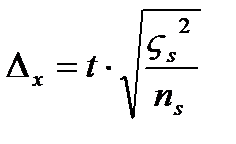
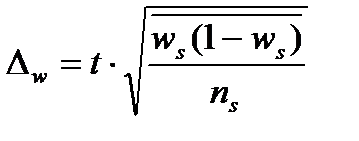
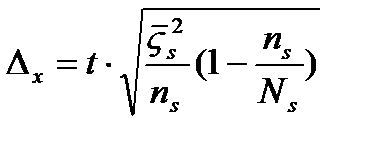
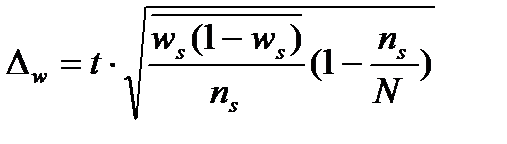
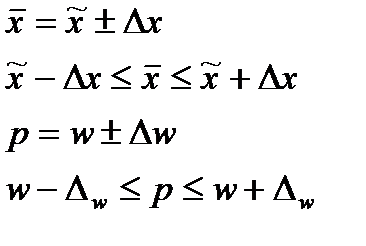
 , где y – среднее значение результативного признака. x – значение факторного признака. a и b параметры уравнения. Причем a это значение y при x =0
, где y – среднее значение результативного признака. x – значение факторного признака. a и b параметры уравнения. Причем a это значение y при x =0
 где все средние показатели рассчитываются по арифметической простоq.
где все средние показатели рассчитываются по арифметической простоq.

 - Коэффициент регрессии
- Коэффициент регрессии

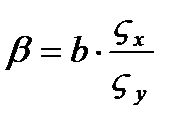
 (дельта) характеризует отклонение групповых средних результативного признака от общей средней.
(дельта) характеризует отклонение групповых средних результативного признака от общей средней.
 – общая дисперсия,
– общая дисперсия, -Средняя из частных или групповых дисперсий
-Средняя из частных или групповых дисперсий – межгрупповая дисперсия.
– межгрупповая дисперсия.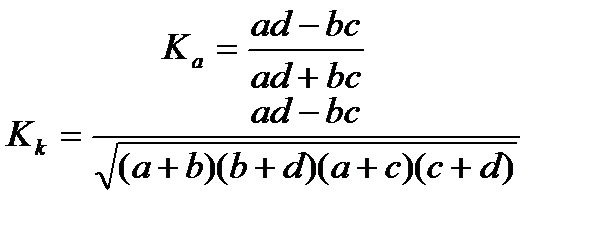
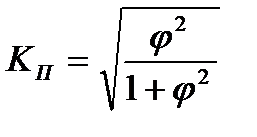
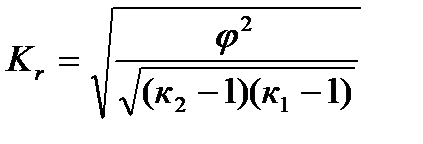
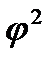 -Показатель взаимной сопряженности, который определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки. (-1)
-Показатель взаимной сопряженности, который определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки. (-1)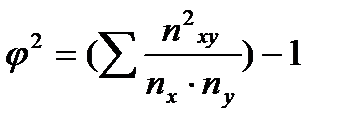
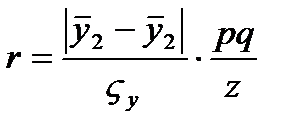
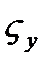 - среднее квадратическое отклонение фактических значений признака от их среднего уровня
- среднее квадратическое отклонение фактических значений признака от их среднего уровня


