
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формулы для расчета численности выборки.Содержание книги Поиск на нашем сайте
А) повторный отбор При расчете средней При определении доли Б) без повторный отбор При расчете средней При определении доли №5 Заключительным этапом выборочного наблюдения является распространение его результатов на генеральную совокупность. Однако часто при статистическом изучении социально-экономический явлений этому процессу предшествует оценка результатов наблюдения с точки зрения самой возможности распространения. Вывод о возможности распространении значительной степени зависит от качества основы выборки и прежде всего от ее полноты. Под полнотой подразумевается наличие и представленность всех типов или групп данной генеральной совокупности в основе выборки. Не полнота основы может привести к нарушению представительности и как следствие не правильным выводом при анализе данных наблюдением. Наиболее точное основы суждения о возможности наблюдения, служит расчет относительной ошибки. Для средней, относительная ошибка рассчитывает по формуле:
Для доли: Если величина относительной ошибки не превышает заранее установленного для данного обследования предельного значения, то данные выборочного наблюдения являются и могут быть распространены на генеральную совокупность. Существуют 2 метода распространения прямой пересчет и способ коэффициентов. Способ прямого пересчета заключается в умножении среднего значения признака найденного в результате выборочного наблюдения на объем генеральной совокупности. Пример. На основании выборочного обследования одной тысячи молодых семей требуется оценить потребность в местах детский яслей. По сколько ясли могут посещать дети в возрасте до 3-х лет…по материалам выборочного обследования необходимо вычислить среднее число детей этого возраста в расчете на одну семью. Допустим величина =0,3. Умножаем 0,3 на численность генеральной совокупности на 1000 молодых семей, получаем 300 лет которые потребуются для обеспечения всех детей местами в яслях. В условиях существования большого числа факторов влияющих на точность результатов выборочного наблюдения. Использования точечной оценки при распространении выборочных характеристик на генеральную совокупность статистических исследований не целесообразно.
Во всех случаях, когда это возможно правильнее пользоваться интервальной оценкой, позволяющей учесть размер предельной ошибки выборки. Если число детей в возрасте до 3-х лет по выборочным данным составило 0,3 на одну семью, а предельная ошибка +-0,3 то требуемое число мест в детский учреждениях будет находиться в пределах от 200 до 400 лет. Способ коэффициентов целесообразно использовать, когда выборочное наблюдение проводится с целью проверки и уточнения данных сплошного наблюдения. Например, численности учтенных единиц совокупности. При этом используют следующую формулу:
Где Y –численность совокупности, 1-с поправкой, 0-без поправки на недоучет. y- Численность совокупности в контрольных точках 0-по первоначальным данным, 1-по данным контрольных мероприятий. При уточнении данных сплошного наблюдения на основе контрольных выборочных мероприятий определяется поправка на недоучет. Метод ее расчета применяется в обследовании относительно не больших совокупностей, когда их объем не превышает нескольких тысяч единиц. ПРИМЕР. При проведении учета коммерческих палаток в городе было зарегистрировано две тысячи единиц. С целью проверки данных сплошного учета были проведены контрольные обходы отдельных районов города. При сплошном учете в этих районах зарегистрировано 400 палаток при контрольном обходе 420. Коэффициент недоучета составил: Y1/Y0=420/400=1.05 следовательно численность палаток с поправкой на недоучет составит Y1-2000*1,05=2100 №6. Малой выборкой называется выборка с небольшим числом единиц(20-30 единиц бывает достаточно), она применяется для оценки на существенность различие результатов между выборками. Существуют два способа оценки малой выборки. 1)оценка по средней разности. Используется для оценки различий между зависимыми наблюдениями. Урожай 2-х сортов (таблица)
Определяют среднюю разность по формуле средней арифметической простой:
Дисперсия разности: Определяют среднюю ошибку средней разности:
Определяют фактическое нормированное отклонение: Находят предельную ошибку средней разности. 2) оценка по разности средних - этот способ используется для независимых экспериментов. Процент качественных изделий.
2 шаг: определяют разность между полученными выборочными средними.
3 шаг: выборочные дисперсии: 4шаг: квадраты средних ошибок:
5шаг: средняя ошибка разности двух средних
6шаг: определить предельную ошибку 7 шаг: Если tф>tт разность между средними существенна. Статистическое изучение взаимосвязи социально-экономических явлений. 1. Понятие и методы изучения статистической связи. 2. Вычисление параметров и применение парной линейной корреляции. 3. Множественная многофакторная регрессия. 4. Оценка значимости параметров взаимосвязи. 5. Методы изучения связи качественных признаков. 6. Ранговые коэффициенты связи. (не параметрические методы изучения связи.) №1 Связи между признаками и явлениями классифицируются по ряду оснований. Признаки в свою очередь по их значению для изучения взаимосвязи делятся на два класса. 1.Признаки обуславливающие изменение других связанных с ними признаков называются факторными. 2.Признаки, изменяющиеся под воздействием факторных являются результативными. Связи между явлениями и признаками дифференцируются по степени тесноты связи, направлению и аналитическому выражению. Кроме того в статистики различают функциональную связь и стохастическую зависимость. Функционально называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака. Функциональная связь проявляется во всех случаях наблюдения и для каждой конкретной единицы исследуемой совокупности, если причиной зависимость проявляется не в каждом отдельном случае, а в среднем при большом числе наблюдений, то такая зависимость называется стохастической. В частном случае стохастической зависимости является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторного признака. По степени тесноты связи различают количественные критерии, ее оценки. Критерии оценки тесноты связи.
По направлению выделяют: связь прямую и обратную. В случае прямой связи с увеличением в значении факторного признака происходит увеличение значения результативного признака и наоборот. В случае обратной связи значение результативного признака изменяется под воздействием факторного в противоположном направлении. По аналитическому выражению выделяют связи прямолинейные, и чаще их называет просто линейные и нелинейные. Если статистическая связь между явлениями может быть приближенно выражена уравнением прямой линии, то ее называют линейной связью. Если же она выражается уравнением, какой-либо кривой линии параболы, гиперболы, степенной или показательной функции, то такую связь называют нелинейной.
Для выявления наличия связи ее характера и направления, в статистике используют следующие методы: 1.метод аналитических группировок 2.приведения параллельных данных. 3.Графический. 4. корреляционный Метод проведения параллельных данных, основан на сопоставлении двух или нескольких рядов статистических величин, такое сопоставление позволяет установить наличие связи и получить представление о ее наличие. Пример.
Прямая. Графический метод. Взаимосвязь между признаками изображается с помощью поля корреляции. (1)(график)
При отсутствии тесных связей имеет место беспорядочное расположение точек на графике, чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи. Для социально-экономических явлений характерно, что наряду с существенный факторами формирующими уровень результативного признака, на него оказывают воздействие многие другие неучтенные случайные факторы, это свидетельствует о том, что взаимосвязь явлений носит корреляционный характер. Корреляция – это статистическая зависимость между случайными величинами не имеющие строго функционального характера, при которой изменения одной из случайных величин приводит к изменению математического ожидания другого. Различают следующие виды корреляции: 1.Парная корреляция -Это связь между двумя признаками, результативным и факторным, или между двумя факторными 2.Частная корреляция это зависимость между результативным и одним факторными признаками, при фиксированном значении других признаков. 3.Множественная корреляция – это зависимость результативного и двух и более факторных признаков включенных в исследование. Корреляционный анализ имеет свои задачи, количественные определения тесноты связи между признаками Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменения зависимой величины или результативного признака, обусловлено влиянием одной или нескольких независимых величин или факторов.
№2 1 способ: Простейшим видом корреляционным связи, является связь между двумя признаками, результативным и факторным. Такая связь называется парной корреляцией и ее можно выразить уравнением прямой линии: B – Коэффициент пропорциональности или регрессии, показывающий на сколько единиц в среднем изменится результативный признак, при изменении факторного признака на одну единицу, значение параметров а и b определяется способом наименьших квадратов путем построения и решения системы двух нормальных уравнений.
Где n – число членов в каждом из двух рядов. Соответствующее значение подставляют в систему уравнений, пользуясь расчетами, проведенными во вспомогательной таблице.
Должно быть минимум 7 наблюдений. n-3 По мимо коэффициента регрессии определяют тесноту или силу связи с помощью коэффициентов корреляции и коэффициента детерминации. Коэффициент корреляции представляет собой величину, которая изменяется в пределах от нуля до -+1. В тех случаях, когда коэффициент корреляции равен нулю, связь отсутствует. Если же равен +или- 1, связь между факторным и результативным признаками функциональная. Знак при коэффициенте корреляции указывает на направление связи, + связь прямая, - обратная. Исчисляют коэффициент корреляции по формуле: Сигма x y –отклонения Коэффициент детерминации D=r^2 Коэффициент детерминации показывает, на сколько процентов вариация результативного признака объясняется колебаниями факторного признака. Данный способ вычисления параметров парной линейной корреляции применяется я в том случае, если исходные данные приведены, по различным объектам, Если же исходная информация представлена в динамике, то есть за несколько периодов времени или на несколько дат, применяется второй способ.
Минимум 7 наблюдений.
Если коэффициент регрессий равен 1,5, значит при увеличении производительности труда (т е фактического признака) на 1000 руб, то Прибыль возрастет на 1,5 тыс руб. Коэффициент корреляции. Вывод: так как r=0.8 то полученное значение коэффициента корреляции позволяет утверждать, что между прибылью и производительностью труда существует прямая тесная взаимосвязь. D=r^2=0,64 Вывод: Значение коэффициента детерминации показывает, что вариация прибыли на 64 % объясняется колебаниями производительности труда. С целью расширения возможности экономического анализа, рассчитывают коэффициент эластичности бета- коэффициент.
Если Э=1,1, то коэффициент эластичности показывает, на сколько процентов изменится значение результативного признака, при изменении факторного признака на 1 %. Вывод: коэффициент эластичности свидетельствует о том, что при увеличении производительности труда на 1 %прибыль возрастет на 1,1%.
бета- коэффициент он показывает, на сколько средних квадратических отклонений изменится результативный признак, при изменении факторного признака на одну сигму. Допустим равна 1,8, при увеличении производительности труда на одно средне квадратическое отклонение прибыль возрастет на одну 1,8 сигма. В случае наличия линейной или не линейной зависимости между двумя признаками для измерения тесноты связи применяют так называемое корреляционное отношение. Различают эмпирическое и теоретическое корреляционное отношение. Эмпирическое корреляционное отношение рассчитывается по данным группировки, когда
Причем все эти дисперсии рассчитываются по результативному признаку.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 306; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.134.33 (0.013 с.) |









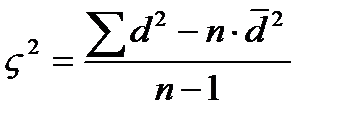

 Полученное значение сравнивают с табличным по таблице Стьюдента. Если tф>tт больше т табличного, величина средней разности статистически достоверна!
Полученное значение сравнивают с табличным по таблице Стьюдента. Если tф>tт больше т табличного, величина средней разности статистически достоверна! Эта величина показывает, на сколько варьирует средняя разность в результате случайных изменений.
Эта величина показывает, на сколько варьирует средняя разность в результате случайных изменений.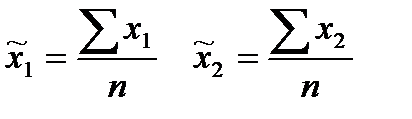





 Если d>E, то различие признака между группами вызвано действием испытываемого фактора.
Если d>E, то различие признака между группами вызвано действием испытываемого фактора. сравнивают с т табличным.
сравнивают с т табличным. , где y – среднее значение результативного признака. x – значение факторного признака. a и b параметры уравнения. Причем a это значение y при x =0
, где y – среднее значение результативного признака. x – значение факторного признака. a и b параметры уравнения. Причем a это значение y при x =0
 где все средние показатели рассчитываются по арифметической простоq.
где все средние показатели рассчитываются по арифметической простоq.

 - Коэффициент регрессии
- Коэффициент регрессии

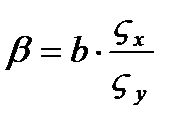
 (дельта) характеризует отклонение групповых средних результативного признака от общей средней.
(дельта) характеризует отклонение групповых средних результативного признака от общей средней.
 – общая дисперсия,
– общая дисперсия, -Средняя из частных или групповых дисперсий
-Средняя из частных или групповых дисперсий – межгрупповая дисперсия.
– межгрупповая дисперсия.


