Различие разделов Кинематика,Статика,Динамика.

Кинематика - раздел механики, в котором изучается механическое движение, без учета масс тел и причин, которые обеспечивают это движение.

Основная задача кинематики - описать движение тела в пространстве в зависимости от времени, не выясняя причин движения.

(Материальная точка, Траектория, Путь, Перемещение..)

Относ:

Равномерное прямолинейное движение.

Равноускоренное прямолинейное движение.

Равномерное движение по окружности.

Криволинейное движение.

Статика - раздел механики, предметом которого являются материальные тела, находящиеся в состоянии покоя при действии на них внешних сил. рассматривается равновесие тел.

(Равновесие тел,момент силы,плечо силы,центр масс,центр тяж.,пара сил)

Виды равновесия: Устойчивое: При малом отклонении тела от положения равновесия возникает сила, стремящаяся возвратить тело в исходное состояние.

Безразличное: При малом отклонении тело остается в равновесии.

Неустойчивое: При малом отклонении тела из положения равновесия возникают силы, стремящиеся увеличить это отклонение.

Дина́мика — раздел механики, в котором изучаются причины возникновения механического движения.

(масса, сила, импульс, энергия.)

· Прямая задача динамики: по заданному характеру движения определить равнодействующую сил, действующих на тело.

· Обратная задача динамики: по заданным силам определить характер движения тела.

·

Моменты сил,его свойства.Гармонические колебания

МОМЕНТ СИЛЫ [Hм] - величина, характеризующая вращательный эффект силы; имеет размерность произведения длины на силу. Различают момент силы относительно центра (точки) и относительно оси.

Какое-либо кинематическое состояние тел, имеющих точку или ось вращения, можно описать моментом силы, характеризующим вращательный эффект действия силы.

Момент силы относительно центра - это векторное произведение радиус – вектора точки приложения силы на вектор силы.

Плечо силы – кратчайшее расстояние от центра до линии действия силы (перпендикуляр из центра на линию действия силы).

Знак момента:

против хода часовой стрелки -„−” (отрицательный)

по часовой стрелке -„+” (положительный);

Свойства момента силы относительно центра (точки).

Модуль момента силы относительно точки равняется удвоенной площади треугольнику построенного на векторах.

Момент силы относительно точки не изменяется при перенесении силы вдоль ее линии действия, поскольку неизменным остается плечо силы.

Момент силы относительно центра (точки) равняется нулю, если:

сила равняется нулю F = 0;

плечо силы h = 0, т.е. линия действия силы проходит через центр.

+свойства
1)момент не меняется при движении точки приложения вдоль линии действия.

2)Момент = 0 если линия действия силы проходит через центр

Теорема Вариньона (о моменте равнодействующей).

Момент равнодействующей плоской системы сходящихся сил относительно какого-либо центра равняется алгебраической сумме моментов составляющих сил системы относительно того же центра.

Моментом пары называется вектор с такими признаками:

он перпендикулярен плоскости пары;

направлен в ту сторону, откуда вращение, которое осуществляет пара, видно против часовой стрелки;

его модуль равняется произведению модуля одной из сил пары на плечо пары с учетом знака

Пара сил – система двух параллельных, равных по модулю и противоположных по направлению сил, приложенных к абсолютно твердому телу.

Момент пары сил равняется произведению модуля одной из сил пары на плечо пары.

Свойство момента пары сил: момент пары равняется моменту одной из сил относительно точки приложения второй силы.

Теоремы о паре сил

* Теорема 1. Пара сил не имеет равнодействующей, т.е. пару сил нельзя заменить одной силой.

*Теорема 2. Пара сил не является системой уравновешенных сил.

* Следствие: пара сил, действующая на абсолютно твердое тело, старается вращать его.

Теорема 3. Сумма моментов сил пары относительно произвольного центра (точки) в пространстве является величиной неизменной и представляет собой вектор-момент этой пары.

Теорема 4. Сумма моментов сил, которые составляют пару, относительно произвольного центра в плоскости действия пары не зависит от центра и равняется произведению силы на плечо пары с учетом знака, т.е. самому моменту пары.

Теорема 5 - об эквивалентности пар. Пары сил, моменты которых равны численно и по знаку, являются эквивалентными. Т.е. пару сил можно заменить или уравновесить только другой эквивалентной парой сил.

Теорема 6 - об уравновешенности пары сил. Пара сил составляет уравновешенную систему сил тогда и только тогда, когда момент пары равняется нулю.

* Теорема 7 - о возможностях перемещения пары сил в плоскости ее действия. Пара сил, полученная перемещениям пары в любое место в плоскости ее действия, эквивалентна предоставленной паре.

Теорема 8 - о добавлении пар сил в плоскости.. для сложения пар сил необходимо сложить их моменты.

 

Пары сил в плоскости уравновешиваются в том случае, если алгебраическая сумма их моментов равняется нулю.

свободные (гармонические) колебания, происходящие под действием линейной восстанавливающей силы, т. е. силы стремящейся вернутьточку в положение равновесия и пропорциональной её отклонению от этого положения равновесия.(F=-kx)

 

 

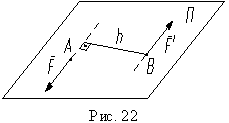
Свойства пары сил.

Пара сил - это система двух равных параллельных сил, направленных в разные стороны (рис. 22).

Свойства пары сил. Первое свойство. Пару сил нельзя привести к силе. Т.е пара сил (как и сила) является самостоятельным элементом статики.

* рассмотрим сложение параллельных сил. Сложим две неравные параллельные силы, направленные в разные стороны (рис. 23). Добавляем к исходной системе сил (F₁,F₂) уравновешенную систему сил (Q₁,Q₂) ~ 0. По аксиоме параллелограмма, силы, приложенные в точках A и B, эквивалентны двум непараллельным силам R₁ и R₂ (рис. 23, a). Согласно следствию второй аксиомы, переносим эти силы в точку пересечения их линий действия C (рис. 23, b). Используя вторую и третью аксиомы, раскладываем силы R₁ и R₂ на составляющие (рис. 23, c), а затем вычитаем уравновешенную систему сил (Q₁,Q₂). В результате получаем, что исходная система сил эквивалентна тем же силам, но приложенным в одной точке C, то есть (F₁,F₂) = (F₁,F₂)_C (рис. 23, d). По аксиоме параллелограмма эта система, а следовательно, и исходная система сил, эквивалентна одной силе или равнодействующей (рис. 23, c):

(1)

*Из рисунков видим, что равнодействующая и ее линия действия CD параллельны исходным силам, а точка D лежит вне отрезка AB.

*При сложении двух параллельных сил, направленных в одну сторону, получается аналогичный результат, только величина равнодействующей будет равна R* = F₁ + F₂, а точка D будет лежать внутри отрезка AB.

*Можно распространить этот вывод и на систему из n параллельных сил, добавляя к полученной равнодействующей по одной из оставшихся сил системы. В результате мы докажем, что

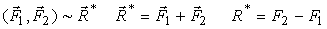
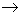* Вернемся к доказательству первого свойства пары сил. Устремим величину первой силы ко второй. При F₁ F₁ из выражений (1) следует, что R* 0, а по рис. 22, a видим, что AC и BC становятся параллельны друг другу. Следовательно, пара сил не может быть приведена к силе или равнодействующей, так как равнодействующая не имеет величины, а ее линия действия не определена, потому что нельзя найти точку C. Таким образом, свойство доказано.