
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зоны Френеля. Построение дифракционных картин графическим способомСодержание книги
Поиск на нашем сайте
Как следует из принципа Гюйгенса- Френеля комплексная амплитуда волны в точке наблюдения
Рассмотрим 'механизм' формирования значения поля Обратим внимание, что комплексная амплитуда поля, создаваемая первой зоной Френеля, определяется вектором, обозначаемым
Если подвергнуть поверхность
Аналогичным образом продолжая разбиение поверхности Границам зон Френеля на спирали соответствуют диаметрально противоположные точки её витков (рис. 5.11c), каждой из которых, соответствуют определяющие её границы радиус на поверхности
где
В частном случае бесконечно удалённого источника от точки наблюдения (
Характерной особенностью спирали (рис. 5.11c) является положение фокуса этой кривой, на который она 'наматывается' при бесконечно большом числе зон Френеля. Покажем, что фокус располагается в центре полуокружности первого витка спирали (рис. 5.11c), т.е. величина, поля создаваемого первой зоной Френеля, в два раза больше величины поля, создаваемой источником Действительно, пусть
Как было отмечено выше, можно считать, что вклады от соседних зон примерно равны и их величины монотонно уменьшаются. По этой причине можно считать выражения в скобках в (5.7) равными нулю, т. е. имеет место равенство для любого
Учитывая, что интенсивность волны пропорциональна квадрату модуля электромагнитных векторов, можно заключить, что интенсивность поля
Четырёхкратное уменьшение интенсивности волны, создаваемой первой зоной Френеля, по отношению к интенсивности волны, создаваемой источником в точке наблюдения, связано с упомянутым выше противофазным вычитанием волн от различных зон Френеля на поверхности волнового фронта. Приближённо, не принимая во внимание уменьшение интенсивности сферической волны с расстоянием, которое она проходит, в расчётах можно полагать, что величиной (5.9) определяется интенсивность волны, создаваемой каждой из зон Френеля, близкой к первой. Это является следствием равенства площадей зон Френеля, соответствующих различным значениям m. Действительно, принимая во внимание (рис. 5.13), находим площадь
Зонная пластинка зонная пластинка Френеля иначе зонная пластинка (англ. Fresnel zone plate) — система чередующихся прозрачных и непрозрачных концентрических колец (зон) с определенными шириной и диаметром, предназначенная для фокусировки излучения по законам волновой оптики. Зонная пластинка Френеля, как и обыкновенная линза, фокусирует параллельный пучок излучения в точку — фокус. У зонной пластинки есть один основной фокус и бесконечное количество побочных фокусов. Разность хода волн от соседних открытых зон до основного фокуса равна длине волны излучения. Фокусировка осуществляется за счет того, что волны от открытых зон приходят в фазе именно в точку фокуса, где происходит их интерференция. Для того чтобы удовлетворить данному условию, необходимо, чтобы радиусы светлых колец были равны где где
где
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 358; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.6.122 (0.006 с.) |

 (рис. 5.4), создаваемая источником монохроматической электромагнитной волны в точке
(рис. 5.4), создаваемая источником монохроматической электромагнитной волны в точке 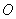 , может быть найдена как суперпозиция комплексных амплитуд сферических волн, испускаемых вторичными источниками на произвольной замкнутой поверхности
, может быть найдена как суперпозиция комплексных амплитуд сферических волн, испускаемых вторичными источниками на произвольной замкнутой поверхности 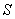 , охватывающей точку
, охватывающей точку  c центром в точке
c центром в точке  в точке наблюдения
в точке наблюдения  , доставляемых электромагнитной волной от бесконечного множества шаровых сегментов
, доставляемых электромагнитной волной от бесконечного множества шаровых сегментов  (рис. 5.10):
(рис. 5.10): .
.

 и совпадающим с диаметром полуокружности, к которой стремится в пределе годограф кривой, представляющей сумму полей, создаваемых бесконечно малыми шаровыми сегментами. Фаза волны, создаваемой первой зоной Френеля, как следует из рис. 5.11a, отстаёт на 90о от фазы волны
и совпадающим с диаметром полуокружности, к которой стремится в пределе годограф кривой, представляющей сумму полей, создаваемых бесконечно малыми шаровыми сегментами. Фаза волны, создаваемой первой зоной Френеля, как следует из рис. 5.11a, отстаёт на 90о от фазы волны  , создаваемой центральным сегментом.
, создаваемой центральным сегментом.

 - ой зоны Френеля (
- ой зоны Френеля ( ) отстоит от прямой
) отстоит от прямой  (рис. 5.12) на расстоянии
(рис. 5.12) на расстоянии  , называемом радиусом
, называемом радиусом 
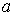 - расстояние вдоль прямой
- расстояние вдоль прямой  - расстояние вдоль прямой
- расстояние вдоль прямой  , для не очень больших
, для не очень больших  :
: .
.


 ) волновой фронт
) волновой фронт  .
.
 - комплексные амплитуды, создаваемые первой, второй и т.д. зонами Френеля. Тогда искомая комплексная амплитуда в точке
- комплексные амплитуды, создаваемые первой, второй и т.д. зонами Френеля. Тогда искомая комплексная амплитуда в точке 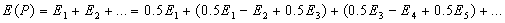
 :
: . Тогда из выражения (5.7) получим:
. Тогда из выражения (5.7) получим:  .
.
 , создаваемого первой зоной Френеля, в четыре раза больше интенсивности волны источника
, создаваемого первой зоной Френеля, в четыре раза больше интенсивности волны источника 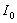 в точке наблюдения, создаваемой всеми вторичными источниками на поверхности
в точке наблюдения, создаваемой всеми вторичными источниками на поверхности 
 сферического сегмента радиуса
сферического сегмента радиуса 
 ,
,
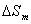 :
: , не зависит от
, не зависит от  ,
, — порядковый номер кольца,
— порядковый номер кольца, 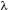 — длина волны излучения,
— длина волны излучения,  — фокусное расстояние. Расстояние до основного фокуса зависит от длины волны падающего излучения и определяется по формуле
— фокусное расстояние. Расстояние до основного фокуса зависит от длины волны падающего излучения и определяется по формуле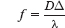 ,
,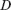 — диаметр линзы,
— диаметр линзы, 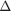 — ширина последнего непрозрачного кольца,
— ширина последнего непрозрачного кольца, 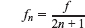 ,
, — целые числа. Разрешение зонной пластинки определяется критерием Релея и приблизительно равно
— целые числа. Разрешение зонной пластинки определяется критерием Релея и приблизительно равно 


