Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Если магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником в отдельности.Содержание книги
Поиск на нашем сайте
Индукцию
Здесь r – расстояние от данного участка Δ l до точки наблюдения, α – угол между направлением на точку наблюдения и направлением тока на данном участке, μ0 – магнитная постоянная. Направление вектора
40. Закон полного тока для магнитного поля. Определение полного тока: Полный ток – это алгебраическая сумма токов, проходящих через ограниченную замкнутым контуром поверхность. В нашем примере полный ток Σ I есть сумма токов I1 и I2: Σ I = I1 + I2 Знаки токов определяем по правилу буравчика. Закон полного тока это закон, связывающий циркуляцию вектора напряженности магнитного поля и ток. Циркуляция вектора напряженности магнитного поля по контуру равна алгебраической сумме токов, охватываемых этим контуром.
Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток протоивоположного направления считается отрицательным.
41. Действие магнитного поля на проводник с током. 42. Действие магнитного поля на движущиеся заряды.
43. Движение заряженной частицы в электрическом и магнитном полях. Траектория частицы. Электрические и магнитные поля действуют на движущиеся заряженные частицы с известной силой. Поэтому эти поля могут использоваться для управления движением заряженных частиц. Потоки движущихся заряженных частиц широко используются в различных приборах, принципы действия и применения некоторых из них мы рассмотрим в данном параграфе. Описание движения заряженной частицы проводится на основании второго закона Ньютона, уравнение которого имеет вид
где qE − сила, действующая на частицу с электрическим зарядом q со стороны электрического поля; qv x B − сила Лоренца, действующая на частицу со стороны магнитного поля. В общем случае напряженность электрического поля E и индукция магнитного поля B могут зависеть от координат (в неоднородных полях) и времени (в нестационарных полях). Для однозначного решения уравнения (1) его необходимо дополнить начальными условиями: положением частицы ro и скоростью vo в некоторый момент времени to.
При описании распространения потоков частиц в некоторых случаях необходимо также учитывать взаимодействия частиц между собой, или принимать во внимание зависимость характеристик полей от положения и скоростей других частиц. Наконец, при записи уравнения (1) принято, что частицы движутся в вакууме, где отсутствуют силы сопротивления среды. Движение частиц в средах, обладающих сопротивлением, описываются в рамках уравнений для электрического тока. При движении частиц в электромагнитном поле, как правило, пренебрегают действием силы тяжести, которая обычно значительно меньше электромагнитных сил. Записанное уравнение движения справедливо для частиц, движущихся со скоростями, значительно меньшими скорости света. В противном случае необходимо использовать релятивистские уравнения движения теории относительности.
44. Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля. Элементарный поток вектора В магнитной индукции (магнитный поток) dФm через малую поверхность площадью dS есть физическая величина равная
Рис. 22 Поток вектора магнитной индукции
Где В – вектор магнитной индукции в точках поверхности dS, n – единичный вектор нормали к площадке dS, Bn =Bcos(B,n) – проекция вектора В на направление нормали. Теорема Гаусса для вектора В: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
Вывод: Этот результат есть математическое подтверждение того, что в природе не существует магнитных зарядов – источников магнитного поля. Эта теорема является, по существу, обобщением опыта. Она выражает собой в постулативной форме тот экспериментальный факт, что линии вектора B не имеют ни начала, ни конца. Поэтому число линий вектора B, выходящих из любого объема, ограниченного замкнутой поверхностью S, всегда равно числу линий, входящих в этот объем.
45. Работа по перемещению проводника с током в магнитном поле. Рассмотрим контур с током, образованный неподвижными проводами и скользящей по ним подвижной перемычкой длиной l (рис. 2.17). Этот контур находится во внешнем однородном магнитном поле
Рис. 2.17 На элемент тока I (подвижный провод) длиной l действует сила Ампера, направленная вправо:
Пусть проводник l переместится параллельно самому себе на расстояние d x. При этом совершится работа:
Итак,
Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником. Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции.
46. Работа по перемещению контура с током в магнитном поле. Выведем выражение для работы по перемещению замкнутого контура с током в магнитном поле. Рассмотрим прямоугольный контур с током 1-2-3-4-1 (рис. 2.18). Магнитное поле направлено от нас перпендикулярно плоскости контура. Магнитный поток
Рис. 2.18 Переместим этот контур параллельно самому себе в новое положение 1'-2'-3'-4'-1'. Магнитное поле в общем случае может быть неоднородным и новый контур будет пронизан магнитным потоком Площадка 4-3-2'-1'-4, расположенная между старым и новым контуром, пронизывается потоком Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура:
где
Провод 1–2 перерезает поток (
Тогда общая работа по перемещению контура
здесь Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока, сцепленного с этим контуром. Элементарную работу по бесконечно малому перемещению контура в магнитном поле можно найти по формуле
Выражения (2.9.1) и (2.9.5) внешне тождественны, но физический смысл величины d Ф различен. Соотношение (2.9.5), выведенное нами для простейшего случая, остаётся справедливым для контура любой формы в произвольном магнитном поле. Более того, если контур неподвижен, а меняется
47. Явление электромагнитной индукции. Закон Фарадея. Правило Ленца.
48. Индуктивность контура. Самоиндукция.
49. Энергия, плотность энергии магнитного поля. Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Если включить электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, то при размыкании ключа наблюдается кратковременная вспышка лампы. Ток в цепи возникает под действием ЭДС самоиндукции. Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Объемная плотность энергии магнитного поля вычисляется по формуле:
где B −− магнитная индукция, μ −− магнитная проницаемость, μ0=4π⋅10−7 Гн/м − магнитная постоянная. Формула для объемной плотности энергии магнитного поля имеет вид, аналогичный выражению для объемной плотности энергии электростатического поля, с тем отличием, что электрические величины заменены в нем магнитными. Магнитная энергия локализована в самом магнитном поле. В однородном магнитном поле в объеме ΔVсодержится энергия: ΔW=wм⋅ΔV. Энергия произвольного магнитного поля может быть найдена путем интегрирования объемной плотности wэwэ по всему объему, в котором создано магнитное поле.
50. Магнитный момент атома. Намагниченность вещества. Электрон, движущийся по орбите, имеет орбитальный момент импульса
Коэффициент пропорциональности g называется гиромагнитным отношением орбитальных моментов и равен
где е, m – заряд и масса электрона. Спину электрона
Величина gs называется гиромагнитным отношением спиновых моментов и равна
Орбитальные и спиновые магнитные моменты электронов образуют магнитный момент атома. Количественной характеристикой намагниченного состояния вещества служит векторная величина – намагниченность (вектор намагниченности) Намагниченность вещества равна отношению магнитного момента макроскопически малого объёма вещества к величине DV этого объёма (т.е. магнитному моменту единицы объема вещества).
где Для однородных и изотропных магнетиков намагниченность пропорциональна индукции внешнего магнитного поля в данной точке:
где c - магнитная восприимчивость вещества (безразмерная величина), характеризующая способность вещества намагничиваться 51. Виды магнетиков: диамагнетики, парамагнетики, ферромагнетики. Магнетики – вещества, которые при внесении во внешнее поле, изменяются так, что сами становятся источниками дополнительного магнитного поля. Намагниченное вещество создает поле Тогда результирующее поле Существуют различные типы намагничивания. Все магнетики подразделяются на диа -, пара -, ферро -, и ферримагнетики. Под действием магнитного поля все элементы объема приобретают магнитный момент. 1) При внесении во внешнее магнитное поле в атомах и молекулах движение электронов изменяется так, что образуется определенным образом ориентированный круговой ток, характеризующийся магнитным моментом. Т.е. молекулы при внесении в магнитное поле приобретают индуцированный магнитный момент, и становится источником дополнительного поля т.е. вещество намагничивается. Такие вещества диамагнетики. 2) Движение электронов таково, что молекулы обладают магнитным моментом в отсутствии магнитного поля. При внесении такого магнетика во внешнее поле, постоянные магнитные моменты отдельных молекул переориентируются в направлении внешнего поля, в результате чего образуется преимущественное направление моментов. Такие вещества парамагнетики. 3) Намагничивание ферромагнетиков связано с тем, что электроны обладают магнитным моментом, находящимся в определенном соотношении с их механическим моментов – спином. Различные механизмы намагничивания приводят к разным зависимостям 1.У диамагнетиков 2. У парамагнетиков 3. У ферромагнетиков 52. Свойства ферромагнетиков. Применение ферромагнетиков.
Кроме уже указанного применения ферромагнетиков для изготовления магнитов, сердечников электромагнитов, трансформаторов, роторов и статоров электрических машин, укажем на их применение для магнитной звукозаписи, магнитной дефектоскопии, обогащения руд. Магнитная звукозапись производится следующим образом (рис. 136). Вблизи ленты, покрытой слоем мелких частиц ферромагнетика, которая медленно перематывается с одного валика на другой, помещается маленький электромагнит, питаемый токами звуковой частоты. Сила тока в его обмотке все время меняется в такт со звуком. Соответственно изменяется и величина индукции магнитного поля, возбуждаемого электромагнитом, отчего остаточная намагниченность ферромагнитной ленты в различных местах оказывается разной. Таким образом, звук оставляет на ленте как бы свои магнитные "отпечатки". Если теперь поставить другой электромагнит вблизи ленты и подсоединить его через усилитель к громкоговорителю, то при движении ленты магнитное поле "отпечатков" будет возбуждать в обмотке электромагнита переменные индукционные токи, которые после усиления и дадут в громкоговорителе звук. Магнитный метод обнаружения брака в деталях, так называемая магнитная дефектоскопия, заключается в следующем. Нарушение однородности в детали (наличие трещин, раковин) приводит к нарушению в ней однородности магнитного поля. Если намагнитить деталь, не имеющую дефекта, то линии индукции будут в ней параллельными, если же в детали имеется дефект, то вследствие различия магнитной проницаемости дефекта и материала изделия параллельность линий индукции нарушается, отчего над дефектом на поверхности детали возникает так называемое магнитное поле дефекта. Нанеся напильником прорези на стальной пластинке, намагнитим ее, а затем поместим в железные опилки. Замечаем, что они прилипают больше по краям прорези. Чтобы узнать, имеет ли деталь дефекты (брак), ее погружают в ванну с минеральным маслом, в котором размешан мелкий ферромагнитный порошок (рис. 137 а). Затем деталь намагничивают электромагнитом, и она замыкает создаваемый им электромагнитный поток. В тех местах, где в детали имеется трещина 7, раковины 2, 3, порошок на поверхности детали распределяется по их краям. Магнитная дефектоскопия получила широкое применение на машиностроительных заводах. В горнорудной промышленности ферромагнитные свойства веществ используются для обогащения руды (рис. 137, б). Раздробленные ее куски попадают на магнитный барабан. Пустая порода не задерживается и сразу скатывается в бункер. Диамагнитная порода притягивается к барабану и в нижней его части под действием силы тяжести падает в другой бункер. Ферромагнитная порода удерживается на барабане, пока ее не счистит специальное приспособление. Если из ферромагнетика, например из железа, сделать кольцо, ящик и поместить их в магнитное поле, то его линии индукции будут проходить только внутри стенок этих предметов. Внутри кольца, ящика магнитное поле будет отсутствовать. Это явление используется для устройства защиты чувствительных измерительных приборов от вреднодействующих на их работу внешних магнитных полей: приборы помещают в сплошной железный корпус (магнитное экранирование).
53. Система уравнений Максвелла для электромагнитного поля. Это фундаментальные уравнения электродинамики покоящихся сред. Уравнения уже приводились ранее, теперь запишем их все вместе. В интегральной форме 1. где
где
2. где
3. где
4. где Электрическое и магнитное поля здесь рассматриваются только вместе (как электромагнитное поле). Для стационарных полей:
Итак, электрическое и магнитное поля в этом случае независимы; поэтому их можно исследовать отдельно (как выполнялось ранее). В дифференциальной форме
Уравнения 1 и 4 - 1-ая пара уравнений Максвелла; уравнения 2 и 3 - 2 -ая пара уравнения Максвелла. Уравнение 1 - по существу закон электромагнитной индукции; оно указывает на изменяющиеся магнитное поле как на один из источников, порождающих электрическое поле. Уравнение 2 показывает, что источниками 54. Свободные гармонические электромагнитные колебания в контуре. Модель предназначена для изучения колебаний, протекающих в идеальном колебательном контуре, изучения графического представления гармонического колебательного движения. Колебательный контур состоит из катушки индуктивностью L и конденсатора емкостью C. В идеальном колебательном контуре активное сопротивление R = 0. Колебательный контур – колебательная система. В контуре происходят периодические изменения энергии электрического поля конденсатора и магнитного поля тока катушки.
В любой момент времени энергия при R = 0: где q и i – мгновенное значение, а q 0 и I 0 – амплитудные значения. Свободные электрические колебания в идеальном колебательном контуре являются гармоническими.
Заряд на конденсаторе изменяется по закону: Учитывая, что U = q / C, можно так же получить уравнение для изменения напряжения на конденсаторе:
Ток в катушке индуктивности: или Период свободных колебаний определяется параметрами самой колебательной системы: индуктивностью и емкостью (формула Томсона):
55. Затухающие электромагнитные колебания. Рассмотрим, например, электрический колебательный контур с активным сопротивлением:
В отличие от ранее рассмотренного идеального контура наличие сопротивления обеспечивает потери электромагнитной энергии в контуре, что ведет к затуханию колебаний. Закон Ома для контура 1-L-R-2 запишется следующим образом (обозначения те же, что и ранее): Сделав в этом уравнении те же подстановки, получим:
где Решением канонического дифференциального уравнения затухающих колебаний величины x является:
В этом уравнении: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 проводника с током можно представить как векторную сумму элементарных индукций
проводника с током можно представить как векторную сумму элементарных индукций 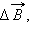 создаваемых отдельными участками проводника. На опыте невозможно выделить отдельный участок проводника с током, так как постоянные токи всегда замкнуты. Можно измерить только суммарную индукцию магнитного поля, создаваемого всеми элементами тока. Закон Био–Савара определяет вклад
создаваемых отдельными участками проводника. На опыте невозможно выделить отдельный участок проводника с током, так как постоянные токи всегда замкнуты. Можно измерить только суммарную индукцию магнитного поля, создаваемого всеми элементами тока. Закон Био–Савара определяет вклад 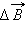 в магнитную индукцию
в магнитную индукцию 
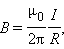



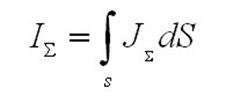






 Роль центростремительной силы играет сила Лоренца:
Роль центростремительной силы играет сила Лоренца: 

 ,
а период обращения
,
а период обращения  не зависит от радиуса окружности!
не зависит от радиуса окружности!




 или
или  [Вб]
[Вб] рис. 23
рис. 23 


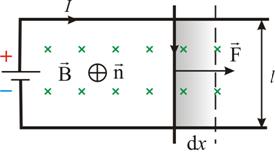
 , перпендикулярном к плоскости контура. При показанном на рисунке направлении тока I, вектор
, перпендикулярном к плоскости контура. При показанном на рисунке направлении тока I, вектор 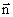 .
.


 ,
,
 , пронизывающий контур, направлен по нормали
, пронизывающий контур, направлен по нормали  .
.
 .
. .
.
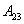 ,
,  равны нулю, т.к. эти стороны не пересекают магнитного потока, при своём перемещение (очерчивают нулевую площадку).
равны нулю, т.к. эти стороны не пересекают магнитного потока, при своём перемещение (очерчивают нулевую площадку). .
. ), но движется против сил действия магнитного поля.
), но движется против сил действия магнитного поля. .
. или
или ,
,
 – это изменение магнитного потока, сцепленного с контуром.
– это изменение магнитного потока, сцепленного с контуром. , то при изменении магнитного потока в контуре на величину dФ, магнитное поле совершает ту же работу
, то при изменении магнитного потока в контуре на величину dФ, магнитное поле совершает ту же работу 
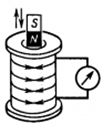


 . e не зависит от свойств контура:
. e не зависит от свойств контура: 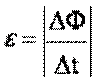 .
ЭДС индукции в замкнутом контуре прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.
.
ЭДС индукции в замкнутом контуре прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.

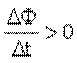 ; Магнитный поток Ф → ΔФ>0.Чтобы компенсировать это изменение (увеличение) внешнего поля, необходимо магнитное поле, направленное в сторону, противоположную внешнему полю:
; Магнитный поток Ф → ΔФ>0.Чтобы компенсировать это изменение (увеличение) внешнего поля, необходимо магнитное поле, направленное в сторону, противоположную внешнему полю: 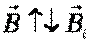 , где
, где 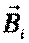 - т.н. индукционное магнитное поле.
В случае 2: при удалении магнита, уменьшении тока, размыкании цепи:
- т.н. индукционное магнитное поле.
В случае 2: при удалении магнита, уменьшении тока, размыкании цепи:  . Магнитный поток Ф→ ΔФ<0. Чтобы компенсировать это изменение (уменьшение), необходимо магнитное поле, сонаправленное с внешним полем:
. Магнитный поток Ф→ ΔФ<0. Чтобы компенсировать это изменение (уменьшение), необходимо магнитное поле, сонаправленное с внешним полем:  .
.
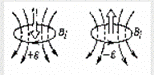
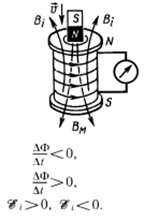
 ),если
),если  (т.е. ΔΦ>0). Ток в контуре имеет положительное направление (
(т.е. ΔΦ>0). Ток в контуре имеет положительное направление ( ), если
), если  .
Данная формула справедлива для СИ (коэффициент пропорциональности равен 1). В других системах единиц коэффициент другой.
.
Данная формула справедлива для СИ (коэффициент пропорциональности равен 1). В других системах единиц коэффициент другой.

 ,
где n – количество витков. Все предыдущие формулы справедливы в случае линейного (равномерного) изменения магнитного потока. В произвольном случае закон записывается через производную:
,
где n – количество витков. Все предыдущие формулы справедливы в случае линейного (равномерного) изменения магнитного потока. В произвольном случае закон записывается через производную:  , где e – мгновенное значение ЭДС индукции.
, где e – мгновенное значение ЭДС индукции.


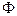 поэтому пропорционален току
поэтому пропорционален току  в контуре:
в контуре: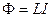 ,
, называется индуктивностью контура. Индуктивность
называется индуктивностью контура. Индуктивность  .
.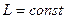 и
и ,
,




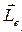 , который противоположен по направлению вектору
, который противоположен по направлению вектору  орбитального магнитного момента электрона (рис. 2.13) и связан с ним соотношением:
орбитального магнитного момента электрона (рис. 2.13) и связан с ним соотношением: .
.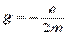 ,
, , пропорциональный спину и направленный в противоположную сторону:
, пропорциональный спину и направленный в противоположную сторону: .
. .
. .
. ,
, - сумма магнитных моментов атомов, находящихся в объеме DV.
- сумма магнитных моментов атомов, находящихся в объеме DV. ,
, ,
,  - внешнее поле.
- внешнее поле.
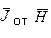 :
: ,т.е. диамагнетик ослабевает внешнее поле.
,т.е. диамагнетик ослабевает внешнее поле.  ~10-5 Диамагнетизм имеется у всех веществ.
~10-5 Диамагнетизм имеется у всех веществ. . Парамагнетизм усиливает поле.
. Парамагнетизм усиливает поле. 
 ,
, 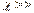 1. У них имеется остаточная намагниченность, т.е. намагниченность образца сохраняется и после того, как внешнее поле стало равно нулю.
1. У них имеется остаточная намагниченность, т.е. намагниченность образца сохраняется и после того, как внешнее поле стало равно нулю.
 ,
, - циркуляция напряженности электрического поля по любому замкнутому контуру;
- циркуляция напряженности электрического поля по любому замкнутому контуру; - производная по времени от магнитного потока через любую поверхность, ограниченную данным контуром.
- производная по времени от магнитного потока через любую поверхность, ограниченную данным контуром. ,
, - электростатическое потенциальное поле,
- электростатическое потенциальное поле, - вихревое поле,
- вихревое поле, .
. ,
, - объ¨мная плотность сторонних зарядов;
- объ¨мная плотность сторонних зарядов; - поток
- поток 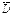 сквозь любую замкнутую поверхность,
сквозь любую замкнутую поверхность,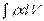 - алгебраическая сумма сторонних зарядов, охватываемой этой поверхностью.
- алгебраическая сумма сторонних зарядов, охватываемой этой поверхностью. ,
,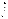 - плотность тока проводимости;
- плотность тока проводимости; - циркуляция
- циркуляция  по любому замкнутому контуру,
по любому замкнутому контуру,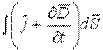 - полный ток через любую поверхность, ограниченную данным контуром.
- полный ток через любую поверхность, ограниченную данным контуром. ,
, - поток вектора
- поток вектора  сквозь произвольную замкнутую поверхность.
сквозь произвольную замкнутую поверхность. ,
, 

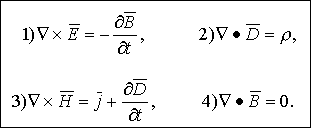 (**) - полевые уравнения
(**) - полевые уравнения находятся
находятся  и
и 


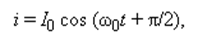




 или
или 
 и
и