
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Таким образом, при параллельном соединении электроемкости складываются.Содержание книги
Поиск на нашем сайте
Вопросы к экзамену по ФИЗИКЕ 1. Предмет классической электродинамики 2. Электростатика. Закон Кулона. 3. Напряжённость электростатического поля 4. Графическое изображение электростатического поля. 5. Поток вектора напряжённости электростатического поля через заданную поверхность. 6. Принцип суперпозиции электростатических полей 7. Теорема Гаусса. 8. Работа электростатического поля. 9. Циркуляция вектора напряжённости электростатического поля. 10. Потенциал электростатического поля. 11. Разность потенциалов электростатического поля. 12. Связь между потенциалом и напряжённостью электростатического поля. 13. Графическое изображение потенциала электростатического поля. 14. Поляризация диэлектриков. 15. Поляризованность диэлектриков. 16. Относительная диэлектрическая проницаемость. Вектор электрического смещения. 17. Проводники в электростатическом поле. 18. Взаимосвязь между напряжённостью поля вблизи поверхности проводника и плотности зарядов на его поверхности. 19. Электростатическая защита. 20. Электроёмкость уединённого проводника 21. Конденсаторы. 22. Электроёмкость плоского конденсатора. 23. Последовательное и параллельное соединение конденсаторов. 24. Энергия системы заряженных тел. 25. Энергия электростатического поля. 26. Постоянный электрический ток. 27. Характеристики постоянного электрического тока 28. Сторонние силы. Эдс. 29. Напряжение на участке цепи. 30. Закон Ома для однородного участка цепи. 31. Работа и мощность электрического тока. 32. Закон Ома для неоднородного участка цепи. 33. Классическая теория электропроводности металлов. 34. Магнитное поле как вид материи. 35. Основные характеристики магнитного поля. 36. Линии магнитной индукции 37. Вектор напряжённости магнитного поля. Принцип суперпозиции. 38. Основные характеристики магнитного поля. Напряженность и индукция магнитного поля. Линии магнитной индукции. 39. Закон Био-Савара-Лапласа и его применение к расчетам магнитного поля. 40. Закон полного тока для магнитного поля. 41. Действие магнитного поля на проводник с током. 42. Действие магнитного поля на движущиеся заряды. 43. Движение заряженной частицы в электрическом и магнитном полях. Траектория частицы. 44. Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля.
45. Работа по перемещению проводника с током в магнитном поле. 46. Работа по перемещению контура с током в магнитном поле. 47. Явление электромагнитной индукции. Закон Фарадея. Правило Ленца. 48. Индуктивность контура. Самоиндукция. 49. Энергия, плотность энергии магнитного поля. 50. Магнитный момент атома. Намагниченность вещества. 51. Виды магнетиков: диамагнетики, парамагнетики, ферромагнетики. 52. Свойства ферромагнетиков. Применение ферромагнетиков. 53. Система уравнений Максвелла для электромагнитного поля. 54. Свободные гармонические электромагнитные колебания в контуре. 55. Затухающие электромагнитные колебания. 56. Вынужденные электромагнитные колебания. Резонанс. 57. Метод векторных диаграмм в цепи переменного тока. 58. Полное сопротивление цепи переменного тока. 59. Мощность в цепи переменного тока. 60. Электромагнитные волны и их свойства. 61. Шкала электромагнитных волн. 62. Основные законы оптики и следствия из них. 63. Когерентность и монохроматичность световых волн. 64. Интерференция от двух когерентных источников. 65. Интерференция в тонких пленках. 66. Интерферометры. 67. Принцип Гюйгенса-Френеля. Метод зон Френеля. 68. Дифракция Френеля на круглом отверстии и диске. 69. Дифракция Фраунгофера на щели и решетке. 70. Естественный и поляризованный свет. 71. Поляризация при отражении и преломлении света. Закон Брюстера. 72. Двойное лучепреломление. Поляроиды и поляризационные призмы. 73. Вращение плоскости поляризации. 74. Дисперсия света. Области нормальной и аномальной дисперсии.
1. Предмет классической электродинамики Электродина́мика — раздел физики, изучающий электромагнитное поле в наиболее общем случае (то есть, рассматриваются переменные поля, зависящие от времени) и его взаимодействие с телами, имеющимиэлектрический заряд (электромагнитное взаимодействие). Предмет электродинамики включает связь электрических и магнитных явлений, электромагнитное излучение (в разных условиях, как свободное, так и в разнообразных случаях взаимодействии с веществом), электрический ток (переменный) и его взаимодействие с электромагнитным полем (электрический ток может быть рассмотрен как совокупность движущихся заряженных частиц). Любое электрическое и магнитное взаимодействие между заряженными телами рассматривается в современной физике как взаимодействие с участием электромагнитного поля и также является предметом электродинамики.
Основные формулы Электродинамики. Закон Кулона:
Разность потенциалов:
Электроемкость:
Энергия конденсатора:
Закон Джоуля – Ленца:
Сила Ампера:
Закон электромагнитной индукции:
Магнитная энергия катушки:
Реактивное сопротивление:
Поле точечного заряда:
Потенциал заряженного шара:
Плоский конденсатор:
Закон Ома:
Сила Лоренца:
Магнитный поток:
Индуктивность:
Колебательный контур:
Мощность переменного тока:
2. Электростатика. Закон Кулона.
Электростатика — раздел учения об электричестве, изучающий взаимодействие неподвижных электрических зарядов. Между одноимённо заряженными телами возникает электростатическое (или кулоновское) отталкивание, а между разноимённо заряженными — электростатическое притяжение. Явление отталкивания одноименных зарядов лежит в основе создания электроскопа — прибора для обнаружения электрических зарядов. Зако́н Куло́на — это закон, описывающий силы взаимодействия между неподвижными точечными электрическими зарядами.
Закон Кулона
F - сила k - коэффициент пропорциональности q1, q2 - заряды r - расстояние
Постоянная Кулона
k - коэффициент пропорциональности ε_0 - электрическая постоянная
3. Напряжённость электростатического поля 4. Графическое изображение электростатического поля.
5. Поток вектора напряжённости электростатического поля через заданную поверхность.
Сначала введем понятие «поток вектора» - это скалярная величина.
Поток вектора
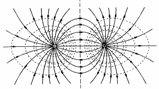
6. Принцип суперпозиции электростатических полей Напряженность поля системы точечных неподвижных зарядов равна векторной сумме напряженностей полей, которые создавали бы каждый из зарядов в отдельности:
В качестве примера рассмотрим поле двух точечных зарядов q1 и q2 (рис. 1.4).
7. Теорема Гаусса. Поток Ф вектора
Если заряд распределен в пространстве с объемной плотностью r, то теорема Гаусса для электрического поля в вакууме:
Рассмотрим некоторые простые примеры вычисления электрического поля с помощью теоремы Гаусса. Чтобы найти напряженность с помощью теоремы Гаусса, нужно взять интеграл. Надо суметь выбрать такую замкнутую поверхность, в каждой точке которой было бы Е = const, и cosa = const. Тогда в левой части теоремы Е и cosa можно будет вынести из-под знака интеграла. Поэтому практически теорему Гаусса можно применить только в следующих случаях: сфера, шар, длинная нить, длинный цилиндр, бесконечная плоскость.
1. Поле равномерно заряженной сферической поверхности
Если r < R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности Е = 0. График зависимости Е от r приведен на рис. 1.10, б.
2. Поле объемно заряженного шара Шар радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью r. Учитывая соображения симметрии, при r ³ R получим, как и в случае сферической поверхности:
3. Поле равномерно заряженной бесконечной плоскости
4. Поле равномерно заряженного бесконечного цилиндра (нити)
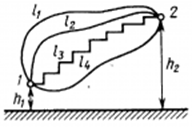
8. Работа электростатического поля.
9. Циркуляция вектора напряжённости электростатического поля. Работа, совершаемая силами электрического поля при перемещении единичного положительного заряда по замкнутому контуру длиной l, определяется как циркуляция вектора напряженности электрического поля:
Так как для замкнутого пути положения начальной и конечной точек перемещения заряда совпадают, то работа сил электрического поля на замкнутом пути равна нулю, а значит, равна нулю и циркуляция вектора напряженности, т.е.
Равенство нулю означает, что силы электрического поля являются силами консервативными, а само поле - потенциальным.
10. Потенциал электростатического поля. 11. Разность потенциалов электростатического поля.
12. Связь между потенциалом и напряжённостью электростатического поля.
13. Графическое изображение потенциала электростатического поля. Хуй знает. Скорее всего смотри п. 4. графическое отображение электромагнитного поля 14. Поляризация диэлектриков. 15. Поляризованность диэлектриков. Все известные в природе вещества, в соответствии с их способностью проводить электрический ток, делятся на три основных класса: диэлектрики, полупроводники и проводники. Если удельное сопротивление у проводников равно В идеальном диэлектрике свободных зарядов, то есть способных перемещаться на значительные расстояния (превосходящие расстояния между атомами), нет. Но это не значит, что диэлектрик, помещенный в электростатическое поле, не реагирует на него, что в нем ничего не происходит. Любое вещество состоит из атомов, образованных положительными ядрами и отрицательными электронами. Поэтому в диэлектриках происходит поляризация. Смещение электрических зарядов вещества под действием электрического поля называется поляризацией. Способность к поляризации является основным свойством диэлектриков. Видов поляризации много. Поляризуемость диэлектрика включает составляющие – электронную, ионную и ориентационную (дипольную). Рис. 4.1 иллюстрирует механизм этих видов поляризуемости.
Рис. 4.1 Электронная поляризуемость обусловлена смещением электронной оболочки атома относительно ядра. Ионная поляризуемость вызвана смещением заряженных ионов по отношению к другим ионам. Ориентационная (дипольная) поляризуемость возникает, когда вещество состоит из молекул, обладающих постоянными электрическими дипольными моментами, которые могут более или менее свободно изменять свою ориентацию во внешнем электрическом поле. Есть и другие виды поляризации. Главное в поляризации – смещение зарядов в электростатическом поле. В результате, каждая молекула или атом образует электрический момент p (рис. 4.2):
Рис. 4.2 Ясно, что электрический момент p пропорционален напряженности Е – напряженности электростатического поля в месте нахождения молекулы, то есть внутри вещества. К чему приводит поляризация? Рассмотрим рис. 4.3.
Рис. 4.3 Внутри диэлектрика электрические заряды диполей компенсируют друг друга. Но на внешних поверхностях диэлектрика, прилегающих к электродам, появляются заряды противоположного знака (поверхностно связанные заряды). Обозначим
Итак, электростатическое поле внутри диэлектрика всегда меньше внешнего поля. Во сколько раз? Рассмотрим некоторые количественные соотношения. Поместим диэлектрик в виде параллелепипеда в электростатическое поле
Рис. 4.4 Электрический момент тела,
где 16. Относительная диэлектрическая проницаемость. Вектор электрического смещения.
Относительная диэлектрическая проницаемость — есть отношение этих значений напряженности электрического поля.
Если напряженность электрического поля E поддерживать постоянной, то при внесении в поле диэлектрика электрическое смещение возрастет от D0 до D. В этом случае относительная диэлектрическая проницаемость определяется следующим образом:
Вектор Электрического смещения Имеем границу раздела двух сред с
а б Рис. 4.10 Как мы уже показали, в соответствии с (4.1.10),
т.е., напряженность электростатического поля E изменяется скачком при переходе из одной среды в другую. Главная задача электростатики – расчет электрических полей, то есть Для упрощения расчетов была введена новая векторная величина – вектор электрического смещения (электрическая индукция):
Из предыдущих рассуждений
Таким образом, вектор
где Таким образом, вектор В СГС: В СИ: Для точечного заряда в вакууме
17. Проводники в электростатическом поле. Вещество, внесенное в электрическое поле, может существенно изменить его. Это связано с тем, что вещество состоит из заряженных частиц. В отсутствие внешнего поля частицы распределяются внутри вещества так, что создаваемое ими электрическое поле в средне
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.128.81 (0.014 с.) |







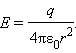
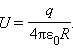

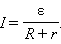



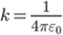

 - величина постоянная в данной точке данного поля.
- величина постоянная в данной точке данного поля.
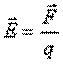 Напряженность - векторная физическая величина, численно равная отношению
силы, действующей на заряд, помещенный в данную точку данного поля, к величине этого заряда.
Напряженность - векторная физическая величина, численно равная отношению
силы, действующей на заряд, помещенный в данную точку данного поля, к величине этого заряда.
 , если q>0.
, если q>0.  , если q<0. Т.е. вектор напряженности направлен от положительного заряда и к отрицательному.
, если q<0. Т.е. вектор напряженности направлен от положительного заряда и к отрицательному.
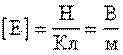 Напряженность в данной точке поля равна 1
Напряженность в данной точке поля равна 1  , если на заряд в 1 Кл, помещенный в эту точку, действует сила в 1 Н. (Напряженность равна 1
, если на заряд в 1 Кл, помещенный в эту точку, действует сила в 1 Н. (Напряженность равна 1  , если между точками электростатического поля, находящимися на расстоянии 1 м друг от друга, существует разность потенциалов 1 В).
, если между точками электростатического поля, находящимися на расстоянии 1 м друг от друга, существует разность потенциалов 1 В).
 (Это опытный факт.)
(Это опытный факт.)
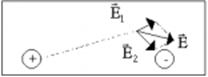



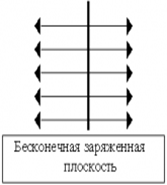
 Рис. 1.9. Поток вектора напряженности через поверхность dS
Рис. 1.9. Поток вектора напряженности через поверхность dS
 которой составляет угол a с вектором
которой составляет угол a с вектором  . Согласно рис. 1.9 dФ определяется как
. Согласно рис. 1.9 dФ определяется как

 – вектор, модуль которого равен dS, направление совпадает с нормалью
– вектор, модуль которого равен dS, направление совпадает с нормалью  к площадке.
к площадке.


 Рис. 1.4. Сложение электрических полей
Рис. 1.4. Сложение электрических полей
 – напряженность поля в точке а, создаваемая зарядом q 1, а
– напряженность поля в точке а, создаваемая зарядом q 1, а  – напряженность поля заряда q 2.
– напряженность поля заряда q 2.  – напряженность результирующего поля.
– напряженность результирующего поля.

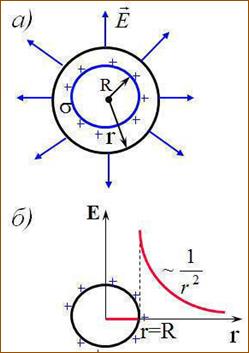 Рис. 1.10. Электрическое поле заряженной сферы
Рис. 1.10. Электрическое поле заряженной сферы
 или
или
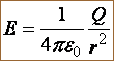
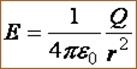
 Рис. 1.11. Зависимость напряженности поля равномерно заряженного шара от расстояния r
Рис. 1.11. Зависимость напряженности поля равномерно заряженного шара от расстояния r

 ,
,

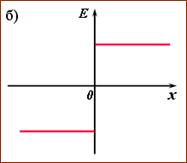 Рис.1.12. Электрическое поле равномерно заряженной плоскости
Рис.1.12. Электрическое поле равномерно заряженной плоскости
 Отсюда напряженность электрического поля равна
Отсюда напряженность электрического поля равна
 .
График зависимости E от r приведен на рис. 1.12 б.
.
График зависимости E от r приведен на рис. 1.12 б.

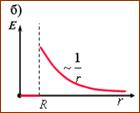 Рис. 1.13. Электрическое поле равномерно заряженного цилиндра
Рис. 1.13. Электрическое поле равномерно заряженного цилиндра
 .
Отсюда при r ³ R
.
Отсюда при r ³ R
 .
Если r < R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области Е = 0.
График зависимости E от r приведен на рис. 1.13 б.
.
Если r < R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области Е = 0.
График зависимости E от r приведен на рис. 1.13 б.
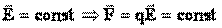 в каждой точке поля.
в каждой точке поля.
 . Следовательно:
. Следовательно: 

 W=qEr
W=qEr

 Т.е. работа равна разности двух эквивалентных величин, зависящих от характера взаимодействия и взаимного расположения. Но мы знаем, что работа - мера изменения энергии. Можно предположить: W=qEr - потенциальная энергия заряда в данной точке электростатического поля. Зависит от выбора начальной точки отсчета потенциальной энергии.
Т.е. работа равна разности двух эквивалентных величин, зависящих от характера взаимодействия и взаимного расположения. Но мы знаем, что работа - мера изменения энергии. Можно предположить: W=qEr - потенциальная энергия заряда в данной точке электростатического поля. Зависит от выбора начальной точки отсчета потенциальной энергии.
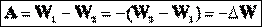 - наиболее общий способ расчета работы в электростатическом поле
- наиболее общий способ расчета работы в электростатическом поле

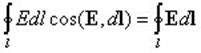
 .
. - энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле.
- энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле.

 - следствие принципа суперпозиции полей (потенциалы складываются алгебраически).
- следствие принципа суперпозиции полей (потенциалы складываются алгебраически).



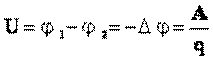

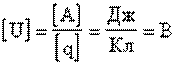 Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж.
Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж.

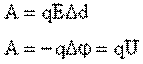 →
→  напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d).
напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d).

 - Напряженность поля равна 1 В/м, если между двумя точками поля, находящимися на расстоянии 1 м друг от друга существует разность потенциалов 1 В.
- Напряженность поля равна 1 В/м, если между двумя точками поля, находящимися на расстоянии 1 м друг от друга существует разность потенциалов 1 В.









 , то у диэлектриков
, то у диэлектриков  , а полупроводники занимают промежуточную область
, а полупроводники занимают промежуточную область 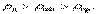





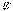 – электростатическое поле связанных зарядов. Оно направлено всегда против внешнего поля
– электростатическое поле связанных зарядов. Оно направлено всегда против внешнего поля 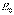 . Следовательно, результирующее электростатическое поле внутри диэлектрика
. Следовательно, результирующее электростатическое поле внутри диэлектрика
 (рис. 4.4).
(рис. 4.4).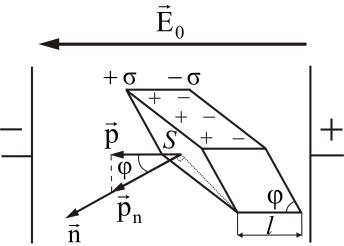
 можно найти по формуле:
можно найти по формуле: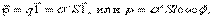
 – поверхностная плотность связанных зарядов.
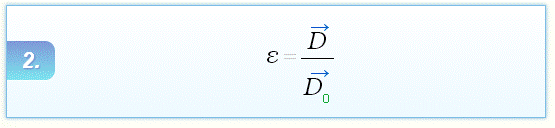
– поверхностная плотность связанных зарядов. Если в электрическое поле поместить непроводник (диэлектрик), то часть электрического смещения будет обусловлена поляризацией диэлектрика. Напряженность электрического поля уменьшится от величины E0 до E(электрическое смещение D остается неизменным).
Если в электрическое поле поместить непроводник (диэлектрик), то часть электрического смещения будет обусловлена поляризацией диэлектрика. Напряженность электрического поля уменьшится от величины E0 до E(электрическое смещение D остается неизменным).
 и
и  , так что,
, так что,  (рис. 4.10, а).
(рис. 4.10, а).
 или
или  ,
,
 , тогда
, тогда  , отсюда
, отсюда
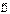 остается неизменным при переходе из одной среды в другую (рис. 4.10, б), и это облегчает расчет
остается неизменным при переходе из одной среды в другую (рис. 4.10, б), и это облегчает расчет 
 , отсюда можно записать:
, отсюда можно записать:
 – вектор поляризации, χ – диэлектрическая восприимчивость среды, характеризующая поляризацию единичного объема среды.
– вектор поляризации, χ – диэлектрическая восприимчивость среды, характеризующая поляризацию единичного объема среды.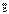 – главной характеристики поля и
– главной характеристики поля и  – поляризации среды.
– поляризации среды. поэтому в вакууме
поэтому в вакууме  и размерность у
и размерность у  , т. е. это заряд, протекающий через единицу поверхности.
, т. е. это заряд, протекающий через единицу поверхности.



