
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Одноступенчатый конический редуктор.Содержание книги
Поиск на нашем сайте
Конические редукторы применяют для передачи движения между валами, оси которых пересекаются обычно под углом 900. Передачи с углом, отличным от 900, встречаются редко. Передаточное число u одноступенчатых конических редукторов с прямозубыми колёсами, как правило, не выше 3-х; в редких случаях U=4. При косых или криволинейных зубьях U=5 (в виде исключения U=6,3). У редукторов с коническими прямозубыми колёсами допускаемая окружная скорость v=5м/с. При более высоких скоростях рекомендуется применять конические колеса с круговыми зубьями, обеспечивающими более плавное зацепление и большую несущую способность.
Выбор электродвигателя Исходные данные: Р2 =1,5 кВт Выбор асинхронного электродвигателя производится по заданной мощности и частоте вращения привода. Требуемая мощность электродвигателя определяется по формуле: Pтр =
η1 = 0,97 – КПД конической передачи [2, т. 1.1,с.5.] η2 = 0,99 – КПД подшипников качения [2, т. 1.1, с 5.] ηε = 0,97 ∙ 0,992 = 0,950 Pтр = nтр = n2 ∙ u n2 = u = 4 – рекомендуемое среднее передаточное число [2,c 7] nтр = 257 ∙ 4=1028 об/мин Принимаем асинхронный электродвигатель серии 4А, типоразмер 100L4. (Рдв = 4,0; nдв = 1500, S = 4,7%). [2, т.п. 1, с. 39] Для дальнейших расчетов принимаем: P1 = Pтр =1,57 кВт n1 = nдв∙(1-S) = 1000 об/мин P2 = 1,5 кВт n2 =257 об/мин Кинематический и силовой расчёт Уточняем передаточное число: u = Принимаем передаточное число по ГОСТ 12289-76: u = 3,89 Определяем кинематические и силовые параметры для ведущего и ведомого валов редуктора. Ведущий вал: n1 = 1429,5 об/мин
P1 = 4,421 кВт М1 = Ведомый вал: n2 = 257 об/мин
Р2 = 1,5 кВт М2 =
Расчёт передачи Исходные данные: P1 = 1,57 кВт P2 = 1,5 кВт
M1 = 10Н · м М2 = 55,55 Н · м n1 = 1000 об/мин n2 = 257 об/мин u = 3,89 Нагрузка: с лёгкими толчками. 1.Выбор материала и назначение ТО.
Шестерня – Сталь 35XM, ТВЧ, HRC 54 Зубчатое колесо – Сталь 50ХН, ТВЧ, HRC 51 [1, т 4.4, с.97]
2.Назначение базы испытания
База испытания при расчёте на контактную прочность: NHO =90 ∙ 10 6 циклов [1, т 4.6, с. 99] Базы испытания на изгибную прочность: NFO =4 • 10 6 циклов [1, c. 102]
3. Определяем циклические долговечности шестерни и колеса NН1 =573∙
NH2 =573∙
4. Коэффициент долговечности на контактную прочность.
KHL=1 так как NH>NHO [1, с. 100]
На изгибную выносливость
KHL=1(1,6≥KF≥ 1) [1, c.101]
5.Вычисление пределов контактной выносливости
Шестерня: σHlimb1 =23HRC= 23×54 = 1242 МПа Колесо: σHlimb2 = 23HRC = 23×51=1173МПа [1, т 4.5, с.99]
6. Пределы изгибной выносливости
Шестерня: σFlimb1 = 800МПа Колесо: σFlimb2 = 750МПа [1, т 4.7, с.102]
7. Определяем допускаемые напряжения.
7.1 Допускаемые контактные напряжения [σH] = σHlimb ∙ZR∙KHL SH SH = 1,1- коэффициент безопасности [1, с.99] ZR = 1 - коэффициент частоты поверхности [1, с.99]
Шестерня: [σH1] = 1242/1,2 = 1035МПа Зуб.Колесо: [σH2] = 1173/1,2 = 977,5 МПа Для расчетов принимаем меньшее значение [σH] = 977,5 МПа
7.2 Допускаемое нормальное напряжение изгиба [σF] = σHlimb ∙YR∙KHL∙KFC SF SF = 2 – коэффициент нагрузки [1, c.101] YR = 1,2 – коэффициент чистоты поверхности [1, c.101] KFC = 1 – коэффициент приложения нагрузки [1, c.101]
[σF1] = 800 ∙1,2 = 480МПа 2 [σF2] = 750 ∙1,2 = 450МПа 8. Определяем среднеделительный диаметр шестерни
Kd = 78МПа – вспомогательный коэффициент [1, c.132] KHB = 1,44 – коэффициент нагрузки при расчёте по контактным напряжениям [1, т.4.9, с. 106]
Ψbd=0,4–коэффициент ширины венца зубчатых колес. [1, т.4.9, с. 106]
9. Определение ширины венца шестерни и колеса:
b1 = Ψbd ∙ d1 = 0,5×47,15 = 23,575 мм
10.Определяем внешний делительный диаметр колеса:
Принимаем по ГОСТ de2 = 160 мм [1, т.4,18, с.133]
11.Определяем внешний модуль закрепления исходя из рекомендуемого числа зубьев шестерни Z1(рекомендуемое) = 18÷30 me = По ГОСТ принимаем внешний модуль зацепления me = 2 мм [1, c.75] 12. Определяем число зубьев шестерни и колеса:
Z2 = Z1 =
13. Уточняем передаточное число: u =
14. Определение углов делительных конусов: tgδ2 = ctgδ1 = u = 3,90 δ2 = 720 42¢ δ1 =90- δ2 = 90 - 72042¢ = 170 18¢ 15. Определяем другие основные параметры передачи:
Внешние диаметры шестерни
de1 = me ∙ z1 = 1×16 = 16 мм dae1 = de1+2me ∙ cosδ1 = 16+2×0,948 = 18мм dfe1 = de1 – 2,4me∙ cosδ1 = 16-2,4∙0,948 = 14мм Внешние диаметры колеса de2 = 63 мм dae2 = de2+2me ∙ cosδ2 = 63+2×0,316= 63,632мм dfe2 = de2 – 2,4me∙ cosδ2 = 63-2,4∙0,316 = 62,241 мм
Средние диаметры шестерни колеса и средний модуль зацепления: d1 = de1 – b∙sinδ1 = 32-23∙0,316 = 2,212 мм m= d2 = m∙ z2 =0,9×63 = 56,7мм
Внешнее конусное расстояние Re =
Среднее конусное расстояние R = Re – 0,5∙b= 25-0,5∙23 = 13,5мм
16. Определение окружной скорости: υ = ω1 ∙ Принимаем 9-ую степень точности [1, т.4.2, c.91]
17. Определение усилий в зацеплении:
Окружные усилия: Ft1 = Ft2 = Радиальная сила шестерни равная осевой силе колеса: Fr1 = Fa = Ft1 ∙ tgα ∙ sinδ1 = 0.364×0.316= 43Н 18. Проверка на контактную прочность σH = zH ∙ zm
zH = 1,76-коэффициент, учитывающий форму сопряжения зубьев
zm = 273МПа1/2 – коэффициент, учитывающий мех.свойства материалов [1, c.132] KHυ = 1,1-коэффициент динамической нагрузки [1, т.4.10, c.107]
σH = 1,76 ∙ 273
= 480,48×0,14×2,03×1,5×1,1=225,31≤ [ %П =
19. Проверка на изгибную прочность:
σF = YF ∙
KFβ = 1,25- коэффициент динамической нагрузки по напряжениям изгиба
Коэффициент формы зубьев принимаются в зависимости от эквивалентного числа зубьев: zυ1 =
zυ2 = Соответственно коэффициент формы зубьев: YF1 = 3,92 YF2 = 3,6 [1, т. 4.14, c.114] Сравниваем отношение: [σF1]/YF1 =
[σF2]/YF2 = Следовательно проверку производим по большему значению, для шестерни:
σF1 = YF1 ∙
σF1 = 3,6 ∙
σF1 = 196МПа < [σF1] = 216 Условие прочности на изгиб выполняется.
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.186.132 (0.01 с.) |

 = 27 c-1
= 27 c-1 ,
, = η1 ∙ η22 – КПД редуктора
= η1 ∙ η22 – КПД редуктора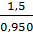 = 1,57кВт.- Необходимая частота вращения электродвигателя
= 1,57кВт.- Необходимая частота вращения электродвигателя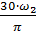 =
=  = 257 об/мин
= 257 об/мин =
=  = 3,89
= 3,89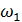 =
=  =
= 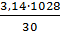 = 107,59 c-1
= 107,59 c-1 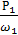 =
=  = 10 Н · м
= 10 Н · м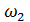 = 27c-1
= 27c-1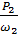 =
=  = 55,55 Н · м
= 55,55 Н · м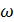 1 = 107,59 c-1
1 = 107,59 c-1  = 36∙103 ч
= 36∙103 ч 1∙
1∙ 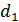 =
= 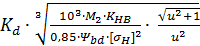
 = 47,15мм
= 47,15мм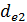 =
= 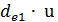 = (
= (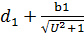 ) × u = (
) × u = (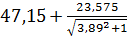 ) = 47,15+5,89=53,04 мм
) = 47,15+5,89=53,04 мм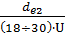 =
=  = (0,9
= (0,9  ÷(30
÷(30 
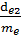 =
= 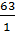 = 63 Принимаем z2=63
= 63 Принимаем z2=63 =
=  = 16,13 Принимаем z1=16,13
= 16,13 Принимаем z1=16,13 =
=  = 3,90
= 3,90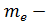
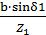 =
= 
 = 0,45 мм
= 0,45 мм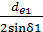 =
= 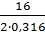 = 25 мм
= 25 мм = 107.59 ×
= 107.59 × 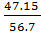 = 89.46 м/с
= 89.46 м/с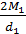 =
=  = 377Н
= 377Н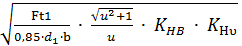 ≤ [
≤ [ 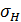 ]
] =
=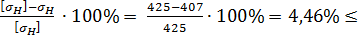 10%-условие проч- ности удовлетворяется.
10%-условие проч- ности удовлетворяется.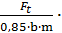 KFβ ∙ KFυ ≤[ σF ]
KFβ ∙ KFυ ≤[ σF ]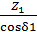 =
= 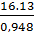 = 17 ,01
= 17 ,01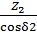 =
=  = 199,36
= 199,36 = 68,8 Мпа
= 68,8 Мпа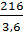 = 60,2 МПа
= 60,2 МПа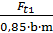 ∙KFβ ∙ KFυ
∙KFβ ∙ KFυ ×1,25 ×1,3=196МПа
×1,25 ×1,3=196МПа


