
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Переполнение разрядной сетки при выполнении алгебраического сложения в обратном и дополнительном кодах.Содержание книги
Поиск на нашем сайте
1) N1>0; N2>0 2) N1<0; N2<0 3) N1>0; N2<0 4) N1<0; N2>0 N1=+0,0111 N1OK=0,0111 N2=+0,1110 N2OK=0,1110 N3OK=1,0101 N3=-0,1010=- N1=-0,0111 N1OK=1,1001 N2=-0,1110 N2OK=1,0010 N3OK=10,1011 N3=+
Методы обнаружения переполнения разрядной сетки. Модифицированные обратный и дополнительный коды. Модифицированное кодирование 00 + 11 –
NМОК= NМДК= N1=-0,1010 N1МОК=11,0101 N2=-0,1000 N2МОК=11,0110 N3МОК=110,1011 N3МОК=10,1100 N1=+0,1010 N1МДК=00,1010 N2=+0,1001 N2МДК=00,1001 N3МДК=01,0011 N1=-0,1010 N1МДК=11,0110 N2=-0,0110 N2МДК=11,1010 N3МДК=111,0000 Модификационные коды упрощают устройство обнаружения переполнения, но вдвое снижают диапазон представления чисел. ±1234567 ±±123456 N1=+0,1110·2+5 N2=+0,1010·2+3 5-3=2 N1=+0,1110·2+5 N2=+0,00101·2+5 N3=(0,11100+0,00101)·2+5=1,00001·2+5 0,00001·2+6 N3=0,10000·22
Логические основы ЭВМ и систем. Понятие логической комбинационной схемы и цифрового автомата. Обработка информации ведется с помощью 2 схем
К комбинационным схемам относятся схемы, в которых выходной сигнал определяется комбинационными сигналами на выходе В цифровом автомате выходной сигнал определяется как действующими входными сигналами, так и сигналами, поступающими в предыдущий момент времени.
Основные законы и задачи алгебры логики.
Задачи: 1. Производить логический анализ схемы. По логической схеме составить описание ее работы логическими выражениями. 2. Выполнить синтез логической схемы, то есть построить оптимальную из простых. 3. Определить логически полный набор логических элементов. 16. Способы задания переключательных функций. Понятие о функционально полных наборах переключательных функций. 1. Таблицей
2. Векторный F=(Y1…Yn) 3. Геометрический Для булевой функции f(x1….xn) вершина булева куба Вn называется единичной если значение функции на этом векторе равно 0. Совокупность всех единичных векторов для функции называется носителем этой функции и обозначается Nf.Чтобы задать перекл. Функцию необходимо перечислить все вершины входящие в этот носитель Nf ….
4. В виде формулы. Понятие о функц. Полных наборах переключательных функций. Функционально полной системой булевых функций (ФПСБФ) называется совокупность таких булефых функций (f1, f2,... fk), что произвольная булева функция f может быть записана в виде формулы через функции этой совокупности. Методы минимизации переключательных функций в базисе И-НЕ; ИЛИ-НЕ; И, ИЛИ, НЕ. Сначала по канонической ДНФ системы булевых функций строится минимальная форма. Для этого используются методы Квайна-Мал-Класки и импликантных матриц, карты Карно и т.д. Затем по минимальной форме находится скобочная форма. Если схема строится из элементов специфичного базиса, например, из элементов И-НЕ, то используются специальные приемы преобразования булевых функций, позволяющие минимизировать затраты оборудования в схемах с учетом специфики функций, реализуемых логическими элементами. Минимальные скобочные представления булевых функций используются в качестве формы для построения комбинационной схемы
Пример. Пусть требуется синтезировать схему операционного элемента, реализующего ПФ Выполним минимизацию этой ПФ с помощью карт Карно. Минимальная форма ПФ имеет вид:
Реализация КС в базисе И, ИЛИ, НЕ представлена на рис. 2.7
Рис. 2.7 Реализация КС в базисе И, ИЛИ, НЕ Если для построения схемы используются элементы универсального базиса, реализующие операции И-НЕ, необходимо булевы функции перевести в базис И-НЕ. Этот перевод функций НЕ, И, ИЛИ выполняется по следующим формулам: (в базисе реализуется функция (2.25)
Рис.2.8.Реализация отрицания, конъюнкции и дизъюнкции в базисе И-НЕ
Реализация отрицания, конъюнкции и дизъюнкции в базисе И-НЕ показана на рис.2.8.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 527; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.154.86 (0.01 с.) |







 =
=  v
v 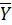
 =X
=X

 ),
),



