
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение кинематических диаграммСодержание книги
Поиск на нашем сайте
Кинематическими диаграммами называют графики зависимости перемещения
точки Построение начнем с диаграммы перемещения и системы координат. На оси абсцисс отложим 12 равных отрезков произвольной величины (1 - 2, 2 - 3, 12 - 13), которые в масштабе Графически продифференцировав эту кривую в определенной последовательности методом хорд, получим диаграмму изменения скорости V(t). 1. Под диаграммой S(t) построим оси координат 1V и 1t, влево от начала оси абсцисс отложим отрезок произвольной длины. 2. Из точки K1 проведем лучи K1l, K12 – K112 параллельно хордам 1 - 2', 2 - 3', 3 - 4' кривой S(Y). Эти лучи отсекут на оси ординат отрезки
3. Из середины соответствующих участков отложим ординаты и получим точки 1", 2", 3" и т. д. Соединив эти точки плавной кривой, получим диаграмму скоростей V(t). Аналогично продифференцировав диаграмму V(t), построим диаграмму ускорений ползуна a(t). Масштабы полученных диаграмм v(t) и а(t) рассчитаем по формулам
Пользуясь диаграммами, определим скорость и ускорение точки С в 3-м положении, а результаты сравним со значениями, рассчитанными по методу планов. Метод диаграмм:
Метод планов:
Разница расчётов составляет:
Ошибки при решении инженерных задач графоаналитическими методами не должны превышать ±5 %. Таким образом, будет достигнута необходимая точность кинематического анализа. Отдельно взятый план скоростей (ускорений) позволяет определить скорости (ускорения) всех точек и звеньев механизма в заданном его положении. Кинематические диаграммы дают возможность проследить
Кинематическое исследование механизма Кинетостатическое исследование механизма проводится с целью определения сил реакций в кинематических парах, уравновешивающей силы и мощности на валу кривошипа. В основе исследования лежат два принципа: Даламбера и статической определимости. Первый применительно к механизмам формулируется следующим образом. Если к механизму приложить все внешние силы, силы реакции в кинематических парах и инерционные нагрузки, его можно рассматривать как механизм, находящийся в равновесии. К нему применимы уравнения статики. Принцип статической определимости заключается в необходимости равенства числа неизвестных составляющих реакций количеству возможных уравнений равновесия. В механизмах статически определимыми являются структурные группы Ассура.
Расчет сил тяжести и инерционных нагрузок В задании на проектирование не указана масса звеньев. Ее следует определять исходя из предположения, что звенья кривошип и шатун 2, выполнен сплошным, круглого поперечного сечения при его полной длине l и массе q, приходящейся на 1 м длины звена; m=ql; q = 20 кг/м, а для ползуна - 3,5 как удвоенная масса кривошипа. Для нашего случая масса звеньев
Силу тяжести звеньев определим по формуле
Силу инерции звеньев рассчитаем по формуле
 - масса соответствующего звена; - масса соответствующего звена;
Моменты сил инерции шатунов найдем по формуле
где Isi - центральный момент инерции, рассчитываемый для круглого поперечного сечения по формуле
где εi - угловое ускорение звена.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.120.103 (0.006 с.) |

 , скорости
, скорости 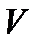 и ускорения, а одной из точек механизма от угла поворота кривошипа
и ускорения, а одной из точек механизма от угла поворота кривошипа  или времени
или времени  . В проекте эти диаграммы строятся для
. В проекте эти диаграммы строятся для и ползуна 3.
и ползуна 3. означают время поворота кривошипа на угол
означают время поворота кривошипа на угол  . Для рассматриваемого варианта длина l отрезка 1 - 13, выражающего время t одного оборота кривошипа, равна мм. Время t определим как
. Для рассматриваемого варианта длина l отрезка 1 - 13, выражающего время t одного оборота кривошипа, равна мм. Время t определим как  масштаб времени
масштаб времени  По оси ординат отложим перемещения ползуна С в масштабе
По оси ординат отложим перемещения ползуна С в масштабе 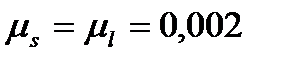 м/мм. Для этого в каждом положении механизма измерим C1C2, C1C3 – C1C12 и отложим их на соответствующих ординатах: 1 - 1', 2 - 2', 7 - 7’диаграммы S(t). Соединив точки 1', 2' - 12' плавной кривой, получим кинематическую диаграмму перемещения ползуна.
м/мм. Для этого в каждом положении механизма измерим C1C2, C1C3 – C1C12 и отложим их на соответствующих ординатах: 1 - 1', 2 - 2', 7 - 7’диаграммы S(t). Соединив точки 1', 2' - 12' плавной кривой, получим кинематическую диаграмму перемещения ползуна.



 = 1,17 м/с;
= 1,17 м/с; 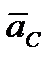 = 4,78 м/с2.
= 4,78 м/с2.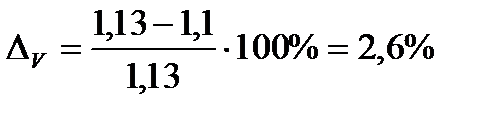


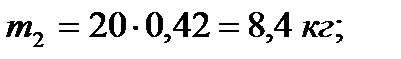

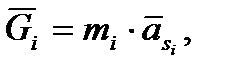




 - ускорение центра массы звена.
- ускорение центра массы звена.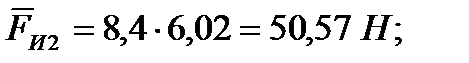

 ,
,
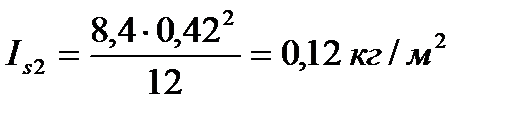 ,
, ;
;


