
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Значения коэффициентов СтьюдентаСодержание книги
Поиск на нашем сайте
Как видно из табл. 1, увеличение числа измерений позволяет при заданной доверительной вероятности существенно уменьшить случайную погрешность. Здесь следует учесть, что, помимо коэффициента an,p, с ростом n уменьшается и значение Sx. Для окончательной оценки величины абсолютной погрешности Δ Х следует теперь сравнить полученную случайную погрешность с погрешностями других видов. Если путем многократных измерений удалось сделать случайную ошибку заметно меньше приборной (при незначительных систематических ошибках), то в качестве Δ Х можно взять приборную погрешность использовавшегося прибора. В противном случае в качестве Δ X берут значение X сл или их сумму. Таким образом, для оценки абсолютной погрешности при прямых измерениях следует: 1) произвести серию измерений искомой величины и вычислить среднее значение 2) вычислить абсолютные ошибки отдельных измерений по формуле ΔXi = | x i - 3) рассчитать S x; 4) определить случайную погрешность Xсл, пользуясь данными табл. 1 (или формулой Стьюдента); 5) сравнить Δ Х сл с приборной погрешностью прибора и взять в качестве абсолютной погрешности Δ Х наибольшую из этих погрешностей; 6) записать результат измерений в виде X = Заметим, что если величины случайной и приборной погрешностей близки друг к другу, то они обе существенно влияют на точность результата, примерно в одинаковой степени. Поэтому в таком случае в качестве максимального значения абсолютной ошибки обычно берут сумму указанных погрешностей. Величина абсолютной погрешности сама по себе дает мало информации о действительной точности измерения, если не сопоставлять ее со значением измеряемой величины. Измерим с погрешностью 5 г вес спичечного коробка и бутылки с молоком. Очевидно, это очень плохая точность для коробка, но избыточная для бутылки. Поэтому, помимо абсолютной погрешности, часто используется относительная погрешность измерения. Она позволяет сопоставить уровень точности измерений для объектов, отличающихся по значениям измеряемых характеристик. Если отсчеты значений делают визуально по линейке или шкале стрелочного прибора, то показания обычно округляют до ближайшего деления шкалы (иногда до половины деления), поскольку отсчитывать на глаз доли деления неудобно и ненадежно. Если случайные ошибки невелики, все измерения после округления дадут один и тот же результат. В таких случаях обязательно следует учесть приборную погрешность. В приборной погрешности различают погрешности отсчета по шкале и погрешности показания прибора. Погрешность отсчета принимают равной половине деления шкалы или половине той доли деления, до которой производится округление. Приближенно можно считать, что такая погрешность соответствует доверительной вероятности a = 0,9. Погрешность показаний, т.е. несоответствие показаний прибора истинному значению измеряемой величины, можно определить при сравнении показаний данного прибора и более точного эталонного прибора. Эта погрешность может быть как систематической (например, неверная градуировка), так и случайной. В паспортных данных приводят максимальное значение суммарной погрешности (систематическая + случайная), которое называют предельной приборной погрешностью. Доверительная вероятность, соответствующая предельной приборной погрешности, близка к единице. Обычно принимают a = 0,997. Вместо предельной погрешности может быть указан класс точности прибора, из которого по известным стандартным соотношениям можно вычислить предельную погрешность. Если класс точности прибора неизвестен и нет паспортных данных, то можно использовать обычно применяемое правило градуировки: предельная погрешность равна цене деления шкалы прибора. Оценка погрешностей при косвенных измерениях имеет некоторую особенность. При косвенных измерениях искомая физическая величина А является функцией величин Х, У, Z,..., которые были получены с помощью прямых измерений. Результат косвенного измерения записывается в виде А ± Δ А, где A = ƒ(X, Y, Z,…) - значение искомой величины, рассчитанное по средним значениям параметров X, Y, Z,..., каждый из которых измеряется по нескольку раз; Δ А - абсолютная погрешность косвенного измерения, зависящая от погрешностей измерения параметров X, Y, Z,... (т.е. от Δ Х, Δ Y, Δ Z,...). В простейших случаях абсолютную и относительную погрешность косвенных измерений подсчитать нетрудно. Рассмотрим несколько примеров. Пусть А = Х + Y. Если известны погрешности Δ X и Δ Y, то А ± Δ А = (X ± ∆ X) + (Y ± ∆ Y). Максимальное значение погрешности равно при этом Δ А = Δ X+ + Δ Y. Такой же будет максимальная абсолютная погрешность, если А = X – Y. Отсюда следует, что относительные погрешности величин, являющихся суммой или разностью двух параметров, равны соответственно: Пусть теперь искомая величина есть произведение A = X ∙ Y. Тогда Обычно последнее слагаемое Δ X ∙Δ Y этой формулы значительно меньше остальных и им можно пренебречь. Тогда:
Для случая, когда A = X / Y, получим При этом максимальное значение погрешности ΔА получится, если погрешности в числителе и в знаменателе взять с разными знаками. Тогда можно записать:
При выводе последней формулы мы пренебрегли членами (Δ Y)2 и Δ X ∙ Δ Y. Максимальная абсолютная погрешность в этом случае равна примерно
а относительная погрешность
Полученные результаты легко обобщаются на произвольное количество сомножителей. Если в самом общем случае где С - постоянный коэффициент, а α, β, γ,... - любые целые или дробные числа, то относительную погрешность косвенного измерения величины А можно записать в виде ПРИЛОЖЕНИЕ 3 ТРЕБОВАНИЯ СТАНДАРТОВ К ВЕСАМ
КЛАССИФИКАЦИЯ ВЕСОВ Согласно ГОСТ 29329-92 весы можно подразделить на следующие группы: По области применения (эксплуатационному назначению): вагонные; вагонеточные; автомобильные; монорельсовые; крановые; товарные; для взвешивания скота; элеваторные; для взвешивания молока; багажные; торговые; медицинские; почтовые. По точности взвешивания: среднего класса точности; обычного класса точности. По способу установки на месте эксплуатации: встроенные; врезные; напольные; настольные; передвижные; подвесные; стационарные. По виду уравновешивающего устройства: электромеханические (электронные); механические. По виду грузоприемного устройства: бункерные; монорельсовые; ковшовые; конвейерные; крюковые; платформенные. По способу достижения положения равновесия: с автоматическим уравновешиванием; с полуавтоматическим уравновешиванием; с неавтоматическим уравновешиванием. В зависимости от вида отсчетного устройства: с аналоговым отсчетным устройством; с дискретным отсчетным устройством. КЛАССЫ ВЕСОВ Согласно ГОСТ 24104-2001 («Весы лабораторные. Общие технические требования». Введен в действие с 01.07.2002 г. Заменил ГОСТ 24104-88) весы могут быть первого, второго и третьего классов. Слово «лабораторные» на практике не ограничивает области применения весов только лабораториями. Названия и обозначения классов:
Цифровые обозначения должны быть выполнены именно римскими цифрами и обязательно в овале (не круге).
Внешний вид некоторых гирь
Классы фактически определяют допустимую погрешность измерений[8] и зависят от следующих параметров весов: · Наибольший предел взвешивания (НПВ) - верхняя граница предела взвешивания, определяющая наибольшую массу, измеряемую при одноразовом взвешивании; · Наименьший предел взвешивания (НмПВ) - нижняя граница предела взвешивания, определяется минимальным грузом, при одноразовом взвешивании которого относительная погрешность взвешивания не должна превышать допустимого значения; · Цена деления d - разность значений массы, соответствующих двум соседним отметкам шкалы весов с аналоговым отсчетным устройством, или значение массы, соответствующее дискретности отсчета цифровых весов; · Цена поверочного деления e - условная величина, выраженная в единицах массы, используемая при классификации весов и нормировании требований к ним; · Число поверочных делений n - значение отношения НПВ/e. Число поверочных делений (n) и значение цены поверочного деления (е) определяют класс точности весов (табл. 1). Таблица 1
Для интервалов взвешивания стандартом установлены пределы допускаемой погрешности (табл. 2). Таблица 2
Цена поверочного деления е выражается через дискретность отсчета весов «d» (цену деления шкалы). Дискретность отсчета весов d выбирается из ряда 1х10а, 2х10а, 5х10а, где а – целое число. Возможные варианты соотношений между е и d: для специального и высокого классов: а) е = d либо б) d < е ≤ 10d. При этом е должно быть из ряда 1х10m, где m – целое число. Но если е * < 0,1 мг, то соотношение между е и d может быть более 10 (20, 50, 100, …). Так, в соответствии с международной рекомендацией OIML R76(1) е ≥ 1 мг. Ограничение связано с неопределенностью (точностью) эталонных гирь. Для весов среднего класса е = d должно быть выполнено всегда. Пользуясь данными вышеприведенных таблиц и паспортными данным на весы, нетрудно определить их класс и погрешность измерений. Пусть, например, имеются весы с НПВ = 2200 г; d = 10 мг; е = 100 мг. Вычислим число поверочных делений: n =НПВ/ е = 22 000. По табл. 1 видим, что это весы высокого (10 000 < n < 100 000) класса точности и НмПВ = 50 d = 500 мг = 0,5 г. Пределы допускаемой погрешности мг можно определить, пользуясь табл. 2. Для рассматриваемого примера (для весов высокого класса точности с е = 100 мг) получим (табл. 3): Таблица 3
До сих пор эксплуатируются весы, выпущенные в период действия ГОСТ 24104-88 (действовал с 01.01.1989 до вступления в силу ГОСТ 24104-2001). Согласно ГОСТ 24104-88 было 4 класса точности: 1, 2, 3, 4. Обозначение классов выполнялось арабскими цифрами. 1 класс – наивысшая точность. В зависимости от наибольшего предела взвешивания и класса точности были назначены абсолютные погрешности. Не было величины е. Можно говорить, что весы 1, 2, 3 (не всегда) классов – это специальный класс по действующему стандарту; часть весов 3 и весы 4 класса – высокий класс. Строгого соответствия нет.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.105.152 (0.007 с.) |

 ;
; и
и  .
.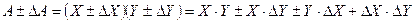 .
.
 или
или  .
. .
. .
. ,
, .
. ,
,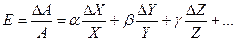 .
. первый (специальный) класс I
первый (специальный) класс I второй (высокий) класс II
второй (высокий) класс II третий (средний) класс III
третий (средний) класс III



