
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Довести, що співвідношення (4.22) справедливо, можна виходячи з (3.17) , (3.20) і (3.21), оскількиСодержание книги
Поиск на нашем сайте
Наприклад, виберемо Р = 17, G = 5, таємний ключ
Отже, відкритий ключ Нехай повідомлення М = {Д}={5}. Виберемо деяке випадкове число K = 3. Перевіримо умову (3.19) дійсно НСД (3,16) =1. Обчислюємо пари чисел а та b:
Таким чином, шифротекстом для літери Д є пара чисел (6,10). Виконаємо розшифрування цього шифротексту. Обчислюємо повідомлення М, використовуючи таємний ключ
Вираз
Можна подати у вигляді
Розв’язуючи дане порівняння, знаходимо М = 5. У реальних схемах шифрування необхідно використовувати як модуль P велике ціле просте число, що має у двійковому поданні довжину від 512 до 1024 бітів. У системі Ель Гамаля відкритого шифрування той самий ступінь захисту, що для алгоритму RSA з модулем N з 200 знаків, досягається вже при модулі P в 150 знаків. Це дозволяє в 5-7 разів збільшити швидкість обробки інформації. Але у такому варіанті відкритого шифрування немає підтвердження достеменності повідомлень. Система Ель Гамаля не позбавлена певних недоліків. Серед них можна зазначити такі: 1 Відсутність семантичної стійкості. Якщо G – примітивний елемент множини
Якщо результат дорівнює 1, то х – квадратичне відрахування за модулем Р, якщо –1, то х – квадратичне невирахування. Далі пасивний зловмисник перевіряє, чи є GK і 2 Подільність шифру. Якщо дано шифрований текст (a, b), можна одержати інший шифрований текст, змінивши тільки другу частину повідомлення. Справді, помноживши b на GU (U ¹0), можна одержати шифротекст для іншого вихідного повідомлення Схема шифрування Рабіна Схема Рабіна була розроблена в 1979 році й може застосовуватися тільки для шифрування даних. Безпека алгоритму спирається на складність пошуку коренів за модулем складеного числа.
Для генерації ключів вибирається пара простих чисел
Ці прості числа і є таємним ключем. Відкритим ключем є число
Для шифрування повідомлення
Для розшифрування повідомлення за допомогою китайської теореми про залишки обчислюється:
Потім вибираються два цілих числа
Чотирма можливими рішеннями є:
Одне із чотирьох результатів, Наприклад, виконаємо шифрування тексту Шифротекст C згідно з (4.25)
Виконаємо розшифрування. Виходячи з (4.26), маємо
Згідно з (4.27)
Тоді за (4.28) одержимо Дійсно, одне із чотирьох значень, а саме:
Керування ключами При симетричному шифруванні обидві сторони, що беруть участь в обміні даними, повинні одержати однакові ключі, до яких сторонні учасники позбавлені доступу. Одночасно із цим необхідна часта зміна ключів, щоб зменшити обсяг даних, що втрачаються через розкриття ключа зловмисником. Тому надійність будь-якої криптосистеми залежить від системи розподілу ключів, що використовується. Система розподілу ключів являє собою систему доставки ключів сторонам, що планують обмін даними, і не дозволяє іншим сторонам скористатися цими ключами. Розподіл ключів можна організувати різними способами. 1 Ключ може бути обраний однією стороною та фізично доставлений іншій стороні, що бере участь у процесі обміну даними. 2 Ключ може вибрати третя сторона та фізично доставити його учасникам обміну. 3 Якщо сторони, які беруть участь в обміні, вже використовують який-небудь ключ, то одна із сторін може передати іншій стороні новий ключ, зашифрований з використанням старого. 4 Якщо обидві сторони обміну мають криптографічно захищені канали і зв'язки із третьою стороною, то остання може доставити ключ учасникам обміну по цих захищених каналах. 5 Ключ може бути генерований обома учасниками обміну з використанням алгоритму генерації. Схеми 1 та 2 припускають передачу ключів з рук у руки. Цей спосіб прийнятний при канальному шифруванні, але у випадку наскрізного шифрування фізична доставка ключа є практично неприйнятною.
Схему 3 можна застосувати як для канального, так і для наскрізного шифрування, але якщо зловмисникові стане коли-небудь відомо значення одного із ключів, то йому стануть відомі і всі наступні ключі. Варіант схеми 4 часто застосовується при наскрізному шифруванні. Так за доставку ключів учасникам обміну відповідає якийсь центр розподілу ключів (ЦРК). При цьому кожен користувач одержує свій унікальний ключ, використовуваний ним разом із ЦРК для організації доставки ключів. Використання ЦРК припускає організацію ієрархії ключів. Зв'язок між ЦРК і учасником майбутнього обміну шифрується з використанням сеансового ключа. Як правило, сеансовий ключ використовують для конкретного логічного з'єднання і надалі більше не застосовують. Сеансовий ключ одержують від центра тими самими каналам, які використовуються для організації зв'язку між кінцевими користувачами – учасниками майбутнього обміну даними. Відповідно сеансові ключі передаються в зашифрованому вигляді, а для шифрування використовують головний ключ, спільний для ЦРК і кінцевого користувача. Прикладом реалізації схеми 5 може бути алгоритм генерації ключів Діффі-Хеллмана. 5.1 Алгоритм шифрування Діффі - Хеллмана Алгоритм Діффі-Хеллмана допомагає обмінюватися секретним ключем для симетричних криптосистем з використанням каналу, захищеного від модифікації, тобто дані, передані цим каналом, можуть бути прослухані, але не змінені. У цьому випадку дві сторони можуть створити однаковий секретний ключ, жодного разу не передавши його по мережі, згідно з таким алгоритмом. Припустимо, що обом учасникам обміну відомі деякі два натуральні числа M і N,де N – просте число. Вони можуть бути відомі й усім іншим зацікавленим особам. Для того щоб створити невідомий більше нікому секретний ключ, обидві сторони генерують випадкові числа: перший абонент – число X, другий абонент – число Y. Потім перший абонент обчислює значення
і пересилає його другому учаснику, а другий учасник обчислює значення
і передає його першому. Зловмисник одержує обидва значення На другому етапі перший абонент, на основі наявного в нього числа X й отриманого по мережі числа
а другий абонент на основі наявних у нього чисел Y та
Неважко переконатися, що в обох учасників вийшло те саме число
Числа Наприклад, нехай абонентам Абонент LA= 113 mod 23=14. Абонент LB= 175 mod 23º21. Абонент А: B: При спробі визначити значення чисел X та Y за перехопленим значенням Ще раз відзначимо, що алгоритм Діффі-Хеллмана працює тільки на лініях зв'язку, надійно захищених від модифікації.
|
||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 233; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.209.122 (0.008 с.) |

 .
.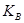 = 2. Обчислюємо
= 2. Обчислюємо .
.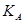 = 8.
= 8.
 .
.
 .
. , то за поліноміальний час можна визначити чи є деяке число x квадратичним відрахуванням. Це робиться піднесенням числа x у степінь
, то за поліноміальний час можна визначити чи є деяке число x квадратичним відрахуванням. Це робиться піднесенням числа x у степінь  за модулем P
за модулем P .
. квадратичними відрахуваннями.
квадратичними відрахуваннями.  буде квадратичним відрахуванням тоді й тільки тоді, коли і GK, і
буде квадратичним відрахуванням тоді й тільки тоді, коли і GK, і  буде квадратичним відрахуванням тоді й тільки тоді, коли саме повідомлення М буде квадратичним відрахуванням. Тобто пасивний зловмисник одержує деяку інформацію про вихідний текст, маючи лише шифрований текст і відкритий ключ одержувача.
буде квадратичним відрахуванням тоді й тільки тоді, коли саме повідомлення М буде квадратичним відрахуванням. Тобто пасивний зловмисник одержує деяку інформацію про вихідний текст, маючи лише шифрований текст і відкритий ключ одержувача. .
. , таких що
, таких що (4.23)
(4.23) . (4.24)
. (4.24) , де
, де  , обчислюється
, обчислюється . (4.25)
. (4.25) (4.26)
(4.26) (4.27)
(4.27) (4.28)
(4.28) і
і  , є повідомлення
, є повідомлення  , використовуючи схему шифрування Рабіна. Згідно з (4.23) виберемо пари чисел
, використовуючи схему шифрування Рабіна. Згідно з (4.23) виберемо пари чисел  й
й  . Тоді, відкритий ключ N =77.
. Тоді, відкритий ключ N =77. .
.




 і є відкритий текст
і є відкритий текст 

 та
та  , але модифікувати їх (втрутитися в процес передачі) не може.
, але модифікувати їх (втрутитися в процес передачі) не може. ,
, .
. :
:
 можуть використовуватися як ключі при обміні даними з використанням традиційних систем шифрування.
можуть використовуватися як ключі при обміні даними з використанням традиційних систем шифрування. і
і  відомі деякі два числа M =17 й N= 23.
відомі деякі два числа M =17 й N= 23. ,
, .
.


