
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Безпека й швидкодія криптосистеми RSAСодержание книги
Поиск на нашем сайте Безпека алгоритму RSA базується на труднощах розв’язання задачі факторизації великих чисел, що є добутками двох великих простих чисел. Дійсно, крипостійкість алгоритму RSA визначається тим, що після формування таємного ключа Розкладання величини N на прості множники Р і Q дозволяє обчислити функцію Іншим можливим способом криптоаналізу алгоритму RSA є безпосереднє обчислення або підбір значення функції
Знаючи j (N), можна визначити х і потім y; знаючи х та y, можна визначити числа P і Q з таких співвідношень:
Однак ця атака не простіша задачі факторизації модуля N. Задача факторизації є задачею, яка важко розв’язується для великих значень модуля N. Спочатку автори алгоритму RSA пропонували для обчислення модуля N вибирати прості числа P й Q випадковим чином, по 50 десяткових розрядів кожне. Вважалося, що такі великі числа N дуже важко розкласти на прості множники. Один з авторів алгоритму RSA, Р.Райвест, вважав, що розкладання на прості множники числа з майже 130 десяткових цифр, наведеного в їхній публікації, зажадає більше 40 квадрильйонів років машинного часу. Однак цей прогноз не виправдався через порівняно швидкий прогрес обчислювальної потужності комп’ютерів, а також поліпшення алгоритмів факторизації. Один з найбільш швидких алгоритмів, відомих у цей час, алгоритм NFS (Number Field Sieve) може виконати факторизацію великого числа N (із числом десяткових розрядів більше 120) за число кроків, оцінюваних величиною
У 1994 р. було факторизовано число з 129 десятковими цифрами. Це вдалося здійснити математикам А.Ленстра й М.Манассі за допомогою організації розподілених обчислень на 1600 комп’ютерах, об’єднаних мережею, протягом восьми місяців. На думку А.Ленстра та М.Манассі, їхня робота компрометує криптосистеми RSA і створює більшу погрозу їхнім подальшим застосуванням. Тепер розроблювачам криптоалгоритмів з відкритим ключем на базі RSA доводиться уникати застосування чисел довжиною менше 200 десяткових розрядів. Останні публікації пропонують застосовувати для цього числа довжиною не менше 300 десяткових розрядів. Схема шифрування Поліга - Хеллмана Схема шифрування Поліга - Хеллмана подібна RSA. Розглянута схема не є симетричним алгоритмом, оскільки використовуються різні ключі для шифрування та розшифрування. З іншого боку її не можна віднести й до класу криптосистем з відкритим ключем, тому що ключі шифрування та розшифрування легко виходять один з одного. Обидва ключі (відкритий і таємний) необхідно тримати в таємниці. Аналогічно схемі RSA криптограма C і відкритий текст M визначаються зі співвідношень:
де
На відміну від алгоритму RSA у цій схемі число N не визначається через два великих простих числа; число N повинне залишатися частиною таємного ключа. Якщо хто-небудь довідається значення Не знаючи значень
Відомо, що це є важкою задачею. Схема шифрування Поліга - Хеллмана запатентована в США [9] і Канаді. Алгоритм шифрування Ель Гамаля Алгоритм Ель Гамаля, розроблено в 1985 р., може бути використаний як для шифрування, так і для цифрових підписів. Безпека схеми Ель Гамаля обумовлена складністю обчислення дискретних логарифмів у кінцевому полі. Для того щоб генерувати пари ключів (відкритий ключ Потім вибирають випадкове ціле число Далі обчислюють відкритий ключ
Для того, щоб зашифрувати повідомлення М, вибирають випадкове ціле число
Потім обчислюють числа
Пари чисел (а,b) є шифротекстом. Помітимо, що довжина шифротексту вдвічі більша довжини вихідного відкритого тексту М. Для того щоб розшифрувати шифротекст (а,b), обчислюють
|
||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 259; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.219.203 (0.007 с.) |

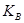 й відкритого ключа
й відкритого ключа 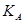 "стираються" значення простих чисел P й Q, і тоді винятково важко визначити таємний ключ
"стираються" значення простих чисел P й Q, і тоді винятково важко визначити таємний ключ 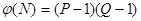 , а потім визначити таємне значення
, а потім визначити таємне значення 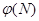 . Якщо встановлено значення
. Якщо встановлено значення  , то співмножники P й Q обчислюються досить просто. Справді, нехай
, то співмножники P й Q обчислюються досить просто. Справді, нехай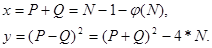
 .
.
 , (4.14)
, (4.14) , (4.15)
, (4.15)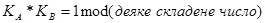 . (4.16)
. (4.16) .
. , причому
, причому 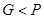 . Числа P й G можуть бути поширені серед групи користувачів.
. Числа P й G можуть бути поширені серед групи користувачів.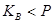 . Число
. Число  . (4.17)
. (4.17) , що задовольняє такі умови:
, що задовольняє такі умови:  , (4.18)
, (4.18) . (4.19)
. (4.19) (4.20)
(4.20)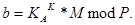 (4.21)
(4.21) . (4.22)
. (4.22)


