
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Концепція криптосистеми з відкритим ключемСодержание книги
Поиск на нашем сайте
Ефективними системами криптографічного захисту даних є асиметричні криптосистеми, які називають також криптосистемами з відкритим ключем. У таких системах для зашифрування даних використовується один ключ, а для розшифрування – інший ключ (звідси й назва – асиметричні). Перший ключ є відкритим і може бути опублікований для використання всіма користувачами системи, які зашифровують дані. Розшифрувати дані за допомогою відкритого ключа неможливо. Для розшифрування даних одержувач зашифрованої інформації використовує другий ключ, що є таємним. Зрозуміло, таємний ключ не може бути визначений, виходячи з відкритого ключа. Узагальнена схема криптосистеми з відкритим ключем показана на рисунку 4.1. В цій криптосистемі застосовують два різних ключі: Генератор ключів доцільно розташовувати на стороні одержувача B, щоб не пересилати таємний ключ Розкриття таємного ключа
Рисунок 4.1 – Узагальнена схема асиметричної криптосистеми Характерні риси асиметричних криптосистем: 1 Відкритий ключ 2 Алгоритми шифрування ( Захист інформації в асиметричній криптосистемі засновано на таємності ключа У.Діффі та М.Хеллман сформулювали вимоги, які забезпечують безпеку асиметричної криптосистеми: 1 Обчислення пари ключів ( 2 Відправник A, знаючи відкритий ключ
3 Одержувач В, використовуючи таємний ключ
4 Зловмисник, знаючи відкритий ключ 5 Зловмисник, знаючи пари ( Односпрямовані функції Концепція асиметричних криптографічних систем з відкритим ключем заснована на застосуванні односпрямованих функцій. Неформально односпрямовану функцію можна визначити в такий спосіб. Нехай Х і Y – деякі довільні множини. Функція Основним критерієм віднесення функції Як приклад односпрямованої функції розглянемо множення цілих чисел. Пряма задача – обчислення добутку двох дуже великих цілих чисел
Є простою задачею для ЕОМ. Зворотна задача – розкладання на множники великого цілого числа, тобто знаходження дільників За сучасними оцінками теорії чисел при цілому Наступний характерний приклад односпрямованої функції – це модульна експонента з фіксованими підставою й модулем. Нехай
Тоді модульна експонента з основою
де Існують ефективні алгоритми, що дозволяють досить швидко обчислити значення функції Якщо Тому, задачу обернення функції Задача дискретного логарифмування формулюється в такий спосіб. Для відомих цілих
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 430; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.72.181 (0.009 с.) |

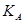 – відкритий ключ відправника A;
– відкритий ключ відправника A; 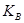 – таємний ключ одержувача В.
– таємний ключ одержувача В.
 ) і розшифрування
) і розшифрування  є відкритими.
є відкритими. . (4.1)
. (4.1) . (4.2)
. (4.2) є односпрямованою, якщо для всіх
є односпрямованою, якщо для всіх  можна легко обчислити функцію
можна легко обчислити функцію  , але для більшості
, але для більшості  досить складно одержати значення
досить складно одержати значення  (при цьому вважають, що існує принаймні одне таке значення
(при цьому вважають, що існує принаймні одне таке значення  ).
). до класу односпрямованих функцій є відсутність ефективних алгоритмів зворотного перетворення
до класу односпрямованих функцій є відсутність ефективних алгоритмів зворотного перетворення  .
. й
й  , тобто знаходження значення
, тобто знаходження значення (4.3)
(4.3) .
. й
й  для розкладання числа
для розкладання числа  й
й  . Визначимо множину
. Визначимо множину 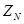
 .
.
 ,
, .
. .
. , то, природно,
, то, природно,  .
. знайти ціле число
знайти ціле число  .
.


