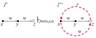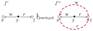Монотонные системы ТМД и их каноническая форма.

Система монотонной ТМД (МТМД) – система ТМД, в командах которой отсутствуют примитивные операторы вида «удалить» и «уничтожить».

Каноническая форма МТМД (КФ МТМД) – система МТМД, в которой команды, содержащие примитивные операторы вида «создать» не содержат условий и примитивных операторов вида «внести».

Теорема 2.1

"МТМД $ эквивалентная ей КФ МТМД.

 

Ациклические монотонные ТМД и алгоритм проверки их безопасности.

Граф создания системы МТМД – ориентированный граф с множеством вершин T, и ребро (u,v) существует если и только если в системе имеется команда, в которой u является родительским, а v – дочерним типом.

Система МТМД (КФМТМД) называется ациклической (АМТМД или, соответственно, АКФМТМД), если ее граф создания не содержит циклов. Иначе говорят, что МТМД (КФМТМД) – циклическая.

Развернутым состоянием АМТМД называется состояние, обеспечиваю-щее минимально необходимый и достаточный для распространения прав доступа набор объектов.

Замкнутым состоянием АМТМД называется состояние, в котором использование команд, не содержащих «создать» не приводит к изменениям в матрице доступа (то есть, состояние, в котором уже невозможно добавлять новые доступы в М, не добавляя в нее объектов).

Пусть α и β – две команды МТМД, содержащие примитивные операторы «создать». Будем считать, что α<β, если и только если для некоторого дочернего типа команды α в графе создания найдется путь в некоторый родительский тип команды β.

Лемма 3.1.

В системе АМТМД отношение «<» является отношением строгого порядка.

Алгоритм 3.2 (проверки безопасности систем АМТМД)

Шаг 1. Перейти к эквивалентной АКФМТМД.

Шаг 2. Используя команды, содержащие примитивные операторы типа «создать», перейти в развернутое состояние согласно Алгоритму 3.1.

Шаг 3. Используя команды, не содержащие операторов типа «создать», перейти в замкнутое состояние и проверить утечку права доступа r.

 

 

Алгоритмическая неразрешимость задачи проверки безопасности систем ХРУ.

Основным фактом, который доказывается в модели ХРУ, является следующая тео­рема.

Теорема 1. Задача проверки безопасности произвольных систем ХРУ алгорит­мически неразрешима.

Задача алгоритмически разрешима, если существует алгоритм, вычисляющий ее хар-ую ф-цию, иначе-алгоритмически неразрешима.

Следует отметить, что в современных КС в большинстве случаев при определении безопасного состояния рассматривается утечка права доступа r не в произвольную, а в заданную ячейку матрицы доступов. Например, появление у администратора без­опасности прав доступа на чтение или модификацию конфигурационных файлов ОС, как правило, не будет являться нарушением безопасности, однако получение данного права доступа нарушителем является нарушением безопасности.

 

11.Классическая модель Take-Grant.

Классическая модель Take-Grant ориентирована на анализ путей распространения прав доступа в системах дискреционного управления доступом. Модель Take-Grant включает в себя следующие элементы:

O – множество объектов системы;

S – множество субъектов системы (SÍO);

R ={r₁,…,r_m}U{t,g}– множество видов прав доступа, где t(take) – право брать права доступа, g(grant) – право давать права доступа;

EÍO´O´R – множество, прав, передаваемых от объекта к объекту;

G=(S,O,E) – конечный помеченный ориентированный граф доступов

Состояние системы описывается графом доступов. При этом возможно наличие прав доступа объектов к объектам.

Основная цель классической Take-Grant – определение и обоснование алгоритмически проверяемых условий проверки возможности утечки права доступа по исходному графу доступов.

Порядок перехода системы Take-Grant из состояние в состояние определяется правилами преобразования графа доступов, носящих название де-юре правил.

В классической модели Take-Grant рассматриваются 4 де-юре правила:

1) take – брать права доступа;

2) grant – давать права доступа;

3) create – создавать новый объект(субъект), причем создатель может взять любые права на созданный объект(субъект) (случаи, когда создается субъект, могут быть оговорены особо);

4) remove – удалять права доступа.

Условия передачи прав доступа при отсутствии ограничений на кооперацию субъектов.

Рассмотрим случай, когда при передаче прав доступа не накладывается ограничений на кооперацию субъектов системы, участвующих в данном процессе.

Пусть x,yÎO₀, x≠y– различные объекты графа доступов G₀=(S₀,O₀,E₀), αÍR.

Определим предикат can_share (α,x,y,G₀)=и Û $ G₁=(S₁,O₁,E₁),…, G_N=(S_N,O_N,E_N), op ₁,…, op_N (N≥0): G₀├ _{op 1}G₁├ _{op 2}…├ _{op N}G_N и (x,y,α)ÌE_N.

Проверка истинности предиката can_share (α,x,y,G₀) в общем случае – алгоритмически неразрешимая задача, т.к. требует проверки всех траекторий функционирования системы.

Определим необходимые и достаточные условия, при которых проверка истинности предиката can_share (α,x,y,G₀) возможна. Эту задачу будем решать в 2 этапа:

1) Определение условий истинности предиката can_share (α,x,y,G₀) для графов, все вершины которых являются субъектами.

2) Определение условий истинности предиката can_share (α,x,y,G₀) для произвольных графов.

Пусть G=(S,S,E) – граф доступов, все вершины – субъекты. Говорят, что вершины являются tg -связанными, или соединенными tg -путем, если в графе между ними существует путь, каждое ребро которого помечено t (take) или g (grant) (без учета направлений ребер).

Теорема 2.1.

Пусть G₀=(S₀,S₀,E₀) – граф доступов, x,yÎS₀, x≠y. Тогда предикат can_share (α,x,y,G₀)=и Û 1)$s₁,…,s_mÎS₀: (s_i,y,g_i)ÌE₀, где i=1,…,m, α=g₁U…U g_m;

2 ) x и s_i – tg- связны в графе G₀, i=1,…,m.

Островом в произвольном графе доступа G0 называется его максималь-ный tg-связный подграф, состоящий из вершин-субъектов.

Мостом в графе доступов G0 называется tg- путь, проходящий через вер-шины-объекты, концами которого являются вершины-субъекты, и словарная запись которого имеет вид (* - многократное, в т.ч. нулевое повторение):

t→*, t←*, t→*, g→, t←*, t→*, g ←,t←*

Начальным пролетом моста в графе доступов G0 называется tg -путь, на-чинающийся в вершине-субъекте, проходящий через вершины-объекты, оканчивающийся в вершине-объекте, словарная запись которого имеет вид: t→*, g→.

Конечным пролетом моста в графе доступов G0 называется tg -путь, начи-нающийся в вершине-объекте, проходящий через вершины-объекты, окан-чивающийся в вершине-субъекте, словарная запись которого имеет вид: t→*.

Теорема 2.2.

Пусть G₀=(S₀,O₀,E₀) – произвольный граф доступов, x,yÎO₀, x≠y. Тогда can_share (α,x,y,G₀)=и Û или (x,y,α) ÌE₀ или выполняются условия:

1) $s₁,…,s_mÎO₀: (s_i,y,g_i)ÌE₀, где i=1,…,m, α=g₁U…U g_m;

2) $x₁’,…,x_m’,s₁’,…,s_m’ÎS₀: a)x=x_i’ или x_i’ соединен с x начальным про-летом моста в графе G₀, i=1,…,m;

б) s_i =s_i’ или s_i’ соединен с s_i конечным пролетом моста в графе G₀, i=1,…,m;

3) в графе G₀ для "(x_i’,s_i’) $ острова I_i1,…,I_iui (u_i≥1): x_i’ÎI_i1,…,s_i’ÎI_iui, и между островами I_ij и I_{i j+1} имеются мосты (j=1,…,u_i-1).

Замечание.

При доказательстве Теоремы 2.2 можно показать, что не существует путей, отличных от мостов, между двумя субъектами, проходящих через вершины-объекты, по которым возможна передача прав доступа.

 

13. Расширенная модель Take-Grant

Де-факто правила расширенной модели Take-Grant

Основные элементы расширенной Take-Grant:

O – множество объектов системы;

S – множество субъектов системы (SÍO);

R ={r₁,…,r_m}U{t,g}U{r,w}– множество видов прав доступа, где r(read) – право или информационный поток на чтение из сущности, w(write) – право или информационный поток на запись в сущность;

EÍO´O´R – множество, прав, передаваемых от объекта к объекту, “реальные” ребра графа, обозначаются сплошными линиями;

FÍO´O´{r,w} – множество информационных потоков, “мнимые” ребра графа, обозначаются пунктирными линиями;

G=(S,O,EUF) – конечный помеченный ориентированный граф доступов и информационных потоков, описывающий состояние системы.

Порядок перехода расширенной Take-Grant из состояние в состояние определяется де-юре и де-факто правилами преобразования графа доступов и информационных потоков.

Если граф G в результате применения правила op преобразован в граф G’, то, как и ранее, будем писать G├ _op G’.

Де-юре правила take, grant, create, remove определяются так же, как в классической T-G и применяются только к «реальным» ребрам G.

Де-факто правила применяются как к «реальным», так и к «мнимым» ребрам, помеченным r или w. Результат применения де-факто правил — добавление новых «мнимых» ребер.

Всего имеется 6 де-факто правил: 2 вспомогательных (первое и второе правила) и 4 основных (spy, find, post, pass).

Первое вспомог правило Второе вспомог правило

 

post(x, y, z) spy(x, y, z)

 

find(x, y, z) pass(x, y, z)