
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устойчивость нсау. Понятие устойчивости по ляпунову.Содержание книги
Поиск на нашем сайте
1)Если все вещественные части корней характеристического уравнения линеаризованной системы отрицательны, то линеаризованная система устойчива. Её невозмущенные движения асимптотически устойчивы и никакие добавки в виде членов с различными нелинейностями не смогут сделать систему неустойчивой. 2)Если по крайней мере один корень линеаризованной системы содержит положительную вещественную часть, то система неустойчива. 3)Если вещественные части корней характеристического уравнения линеаризованной системы равны 0, то свойство устойчивости линеаризованной системы будет неопределенным (система на границе устойчивости). Импульсные САУ. Виды квантования. Определение: Импульсные системы – это такие САУ, в которых имеются сигналы квантованные по времени. Импульсную САУ можно в общем случае представить блок-схемой: εyx
ИЭ – импульсный элемент; НЧ – непрерывная часть. Возможны и более сложные импульсные САУ с несколькими ИЭ, однако в лекциях мы рассмотрим лишь САУ с одним ИЭ. Определение: Квантование, осуществляемое ИЭ в виде преобразовния непрерывного сигнала в последовательность импульсов, называется импульсной модуляцией. Существует три вида импульсной модуляции: 1. амплитудно-импульсная (АИМ); 2. широтно-импульсная (ШИМ); 3. время-импульсная (ВИМ); 3.1. фазо-импульсная (ФИМ); 3.2. частотно-импульсная (ЧИМ). Сущность каждого вида модуляции поясняется на рис Входной сигнал (его величина) называется моделирующим сигналом ИЭ. Модулируемыми параметрами выходного сигнала ИЭ могут служить высота (амплитуда), ширина и период повторения импульса.
38 Z-преобразование или дискретное преобразование Лапласа. Преобразование Лапласа и z-преобразование вычислить z-образн. и z-предаточную ф-цию, которая аналогична комплексной ф-ции W(jω).
Алгоритм перехода
Для того чтобы выбрать время T, нужно применить теорему Котельникова. Частота дискретизации непрерывного сигнала должна не менее чем в 2 раза превышать макс. частоту, содержащуюся в спектре исходного сигнала.
Выбор частоты дискретизации: 1. Исходя из max частоты пропускания самого высокочастотного и звеньев. Сложность передат. ф-ции напрямую осу Передаточные функции разомкнутой и замкнутой импульсной САУ. Характеристические уравнения систем Типовая структура замкнутой САУ, передаточная функция и характеристическое уравнение разомкнутой системы.
Для линейных систем применим принцип суперпозиции воздействий (независимых воздействий).
Для нахождения характеристического уравнения замкнутой системы необходимо также приравнять к нулю знаменатель передаточной функции замкнутой системы
Характеристическое уравнение замкнутой системы может быть получено приравниванием к 0 суммы числителя и знаменателя передаточной функции разомкнутой системы. Устойчивость ИСАУ. Если условия (4) для импульсных САУ не выполняются, то она, как уже было сказано, должна исследоваться либо по дискретным передаточным функциям, либо по частотным характеристикам. Отметим, что исследование устойчивости импульсных САУ осуществляется с помощью известных критериев Рауса, Гурвица, Найквиста, Михайлова модифицированных с учетом особенности работы импульсных систем. Допустим, имеем импульсную САУ вида
Импульсная передаточная функция разомкнутой системы
По правилам преобразования структур, передаточная функция замкнутой системы
Рассмотрим характеристическое уравнение импульсной системы
Так как
то характеристическое уравнение (3) имеет бесчисленное множество корней.
Следовательно, передаточная функция Чтобы импульсная система была устойчивой, необходимо и достаточно, чтобы все полюсы
Если перейти от комплексной плоскости q к плоскости Z=eq, то интересующая нас полоса от −π до отображается в окружность единичного радиуса с центром в начале координат, т.к. при Чтобы импульсная система была устойчивой, необходимо и достаточно, чтобы все полюсы Чтобы применить алгебраические критерии устойчивости к импульсной системе, производят замену переменной, вводя новую переменную r
Область устойчивости импульсной системы в плоскости новой переменной r соответствует вся левая полуплоскость, а границей устойчивости является вся мнимая ось.
В результате подстановки (5) в характеристическое уравнение импульсной системы (3) получаем условия устойчивости, аналогичные непрерывным системам. Следовательно можно применять и любые критерии устойчивости для непрерывных систем. Рассмотрим примеры: 1. Имеем характеристическое уравнение первого порядка
Подставляя (5) в (1п), получим
Для устойчивости рассматриваемой системы, из свойств алгебраических критериев устойчивости, можно записать:
2. Имеем характеристическое уравнение второго порядка
Подставляем (4п) в соотношение (5)
После преобразования получим
Для устойчивости системы необходимо и достаточно, чтобы все коэффициенты (5п) были положительны, т.е.
Аналогично получают условия устойчивости для систем более высокого порядка. Однако для порядка выше 3-го значительно возрастают вычислительные трудности.
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 196; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.98.111 (0.01 с.) |




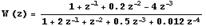

 на выходе
на выходе
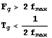

 – передаточная функция разомкнутой системы.
– передаточная функция разомкнутой системы. - Передаточная функция замкнутой системы относительно регулирующей величины по задающему воздействию.
- Передаточная функция замкнутой системы относительно регулирующей величины по задающему воздействию.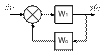
 – передаточная функция замкнутой системы относительно задающей величины по возмущающему воздействию.
– передаточная функция замкнутой системы относительно задающей величины по возмущающему воздействию. – передаточная функция замкнутой системы относительно ошибки регулирования, по задающему воздействию.
– передаточная функция замкнутой системы относительно ошибки регулирования, по задающему воздействию. – передаточная функция замкнутой системы относительно ошибки регулирования, по возмущающему воздействию.
– передаточная функция замкнутой системы относительно ошибки регулирования, по возмущающему воздействию. – передаточная функция разомкнутой системы
– передаточная функция разомкнутой системы
 – Характеристическое уравнение разомкнутой системы получается приравниванием к нулю знаменателя передаточной функции разомкнутой системы.
– Характеристическое уравнение разомкнутой системы получается приравниванием к нулю знаменателя передаточной функции разомкнутой системы.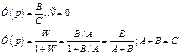




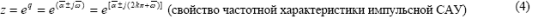

 является также периодической функцией вдоль мнимой оси (оси частот), и поэтому при изучении полюсов этой передаточной функции в комплексной плоскости достаточно рассмотреть их в полосе от −π до +π (рис.191).
является также периодической функцией вдоль мнимой оси (оси частот), и поэтому при изучении полюсов этой передаточной функции в комплексной плоскости достаточно рассмотреть их в полосе от −π до +π (рис.191). при изменении частоты от - π до +π лежали в левой полуплоскости комплексной плоскости (рис.191).
при изменении частоты от - π до +π лежали в левой полуплоскости комплексной плоскости (рис.191).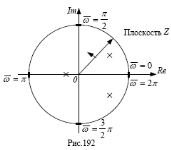
 (мнимая ось) модуль
(мнимая ось) модуль  (рис.192).
(рис.192).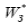 лежали внутри окружности единичного радиуса в комплексной плоскости Z(рис.192).
лежали внутри окружности единичного радиуса в комплексной плоскости Z(рис.192).










