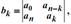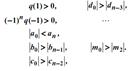Устойчивость исау. Аналог критерия рауса.

Устойчивость ИСАУ. Аналог критерия Гурвица.

Критерий устойчивости Джури является аналогом критерия Рауса –Гурвица. Смысл критерия состоит в следующем.

Пусть характеристическое уравнение цифровой системы имеет вид

 

Чтобы воспользоваться критерием Джури, необходимо вычислить коэффициенты, приведенные в табл

 

Обратим внимание, что элементы второй строки, четвертой строки и т. д. совпадают с элементами первой строки, третьей строки и т. д., но в обратном порядке. Элементы первых двух строк образуются из коэффициентов характеристического уравнения, а элементы последующих строк вычисляются как определители

Необходимые и достаточные условия того, что все корни q(Z)расположены внутри единичной окружности, состоят в следующем:

 

Заметим, что для системы второго порядка массив содержит только одну строку, поэтому никаких дополнительных вычислений не требуется. При увеличении порядка системы на единицу в массив необходимо добавить еще две строки. Для системы n -го порядка, где n>1, существует n+1 ограничений.

Оптимальные и адаптивные САУ.

Системы, в которых обеспечено оптимальное значение какого-либо основного показателя качества работы системы – критерия оптимальности, называется оптимальными САУ.

В качестве критерия эффективности оптимальных САУ может быть: один из показателей качества переходного процесса, точность в установившихся режимах, потребляемая мощность, себестоимость продукции и т.п.

Примеры оптимальных САУ:

1. СУ полетом самолета, обеспечивающая минимальный расход горючего на заданном маршруте.

2. СУ курсом корабля, осуществляющая максимально быстрое изменение курса при наличии ограничений угла поворота и скорости перекидки руля.

Определение: Системы, которые автоматически приспосабливаются к изменению внешних условий и свойств ОУ, обеспечивая при этом необходимое качество управления путем изменения схемы и параметров УУ называются адаптивными САУ. Качество управления численно определяется критерием качества J, который оценивает заранее выбранный, наиболее важный показатель работы САУ.

Критерием качества J может быть: показатель точности работы САУ, производительность, экономичность и т.п.

В общем случае критерий качества, так же как и критерий оптимальности в оптимальных САУ, представляет собой функционал, зависящий от входных и выходных координат системы. В простейших случаях J может быть просто функцией. Примером изменяющихся внешних условий, требующих применения адаптивной САУ, являются нестационарные случайные внешние воздействия на систему, характеристики которых (например, спектральная плотность) изменяются в широких пределах. Примером объекта с переменными параметрами, тоже требующего адаптивной САУ, является самолет или ракета. Действительно, на разных участках полета изменяются динамические характеристики самого объекта в очень широких пределах, т.к. изменяется масса объекта из-за уменьшения запаса горючего, изменяется форма ОУ и т.п. Поэтому обычная САУ не может выполнить свои функции без изменения настройки или схемы УУ. Кроме того, областью применения адаптивных САУ является также ОУ с недостаточно известными свойствами или условиями работы.

Адаптивные САУ подразделяются:

1. САУ со стабилизацией критерия качества (J поддерживается на определенном уровне);

2. САУ с оптимизацией критерия качества (J поддерживается на оптимальном значении);

 

Кроме того адаптивные САУ подразделяются:

1. Самонастраивающиеся (изменяются значения параметров УУ₀);

2. Самоорганизующиеся (изменяется структура УУ₀).

Многомерные САУ. Математическое описание.

Многомерные САУ. Структурные представления.

Наблюдаемость и управляемость. Наблюдаемость.

Наблюдаемость и управляемость. Управляемость.

Наблюдаемость и управляемость. Принцип двойственности в теории управляемости и наблюдаемости.

Критерии оптимизации управления.

Классическое вариационное исчисление. Постановка задачи.